特征选择：卡方检验、F 检验和互信息

时间：2019-03-08 09:32:51 阅读：2186 评论：0 收藏：0 [点我收藏+]

特征选择是特征工程中的重要一环，其主要目的是从所有特征中选出相关特征 (relevant feature)，或者说在不引起重要信息丢失的前提下去除掉无关特征 (irrelevant feature) 和冗余特征 (redundant feature)。进行特征选择的好处主要有以下几种：

降低过拟合风险，提升模型效果
提高训练速度，降低运算开销
更少的特征通常意味着更好的可解释性

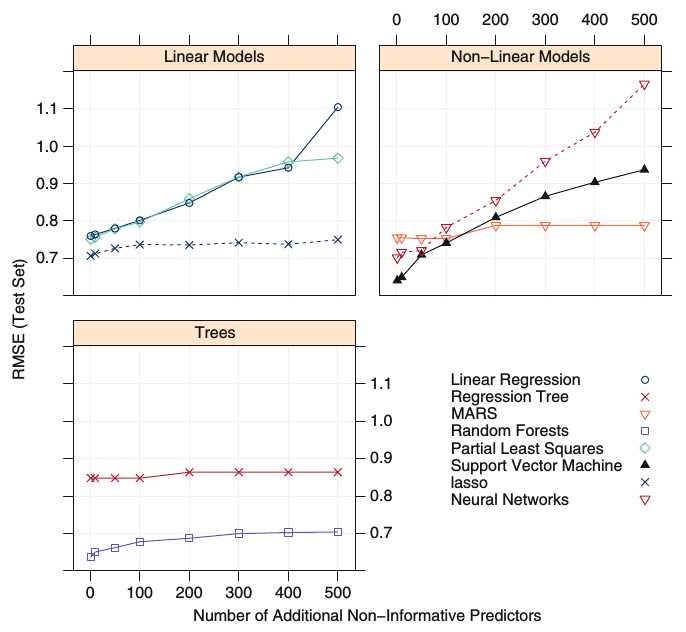
不同的模型对于无关特征的容忍度不同，下图来自《 Applied Predictive Modeling 》 (P489)，显示了逐渐增加无关特征后不同模型的RMSE的变化。树模型普遍表现较好，而神经网络因其模型的复杂性则很容易过拟合。Lasso 因其可以产生稀疏特征因而也有较好的表现。

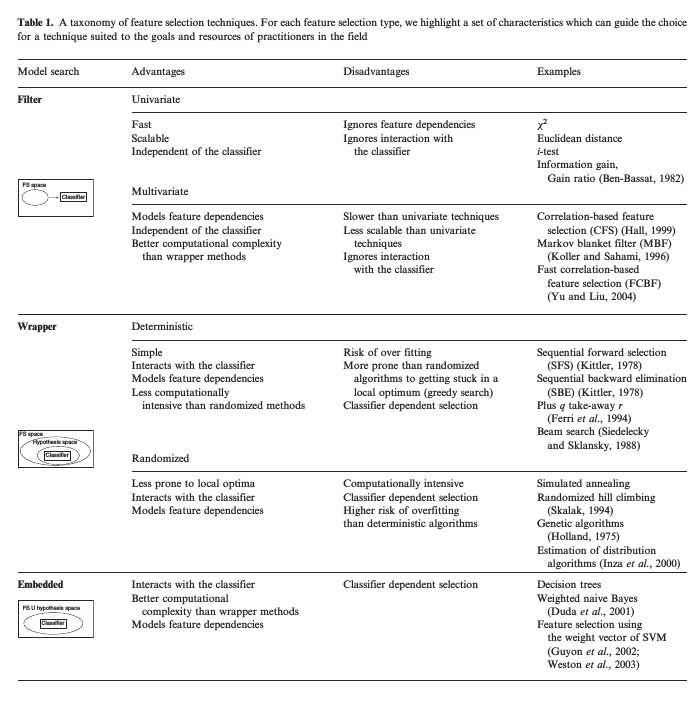
特征选择的方法主要分为三大类：过滤式方法 (Filter Methods)，包裹式方法 (Wrapper Methods) 和嵌入式方法 (Embedded Methods)。

过滤式方法运用统计指标来为每个特征打分并筛选特征，其聚焦于数据本身的特点。其优点是计算快，不依赖于具体的模型，缺点是选择的统计指标不是为特定模型定制的，因而最后的准确率可能不高。而且因为进行的是单变量统计检验，没有考虑特征间的相互关系。
包裹式方法使用模型来筛选特征，通过不断地增加或删除特征，在验证集上测试模型准确率，寻找最优的特征子集。包裹式方法因为有模型的直接参与，因而通常准确性较高，但是因为每变动一个特征都要重新训练模型，因而计算开销大，其另一个缺点是容易过拟合。
嵌入式方法利用了模型本身的特性，将特征选择嵌入到模型的构建过程中。典型的如 Lasso 和树模型等。准确率较高，计算复杂度介于过滤式和包裹式方法之间，但缺点是只有部分模型有这个功能。

下面这张图总结地更加全面，来自《A review of feature selection techniques in bioinformatics 》

本文接下来主要考察过滤式方法中常用的几个方法：卡方检验、F 检验和互信息，并探讨它们用于特征选择的内在机理。

卡方检验

既然特征选择的目的是去除无关特征，那么什么是无关特征？对于分类问题，在过滤式方法中一般假设与标签独立的特征为无关特征，而卡方检验恰好可以进行独立性检验，所以其适用于特征选择。如果检验结果是某个特征与标签独立，则可以去除该特征。说到卡方检验自然会用到卡方分布，其定义如下：

设随机变量 $x_1, x_2 ... x_n \,,\quad \text{i.i.d} \sim N(0,1)$ ，即独立同分布于标准正态分布，那么这 $n$ 个随机变量的平方和：
\[ X = \sum\limits_{i=1}^n x_i^2 \]
构成一个新的随机变量，其服从自由度为 $n$ 的卡方分布 ( $\chi^2$ 分布) ，记为 $X \sim \chi^2_n$ 。

下图显示不同自由度下卡方分布的概率密度曲线，可以看到自由度越大，卡方分布就越接近正态分布：

下面举个例子看卡方检验的一般流程：

假设我想检验一个男人有特殊着装癖好与其变态与否的关系，如果检验的结果是二者不独立，那下次在街上看见女装大佬我可能就要绕着走了。。。所以该独立性检验的假设如下：

零假设 ($H_0$)：着装偏好与变态倾向独立备选假设 ($H_1$) ：着装偏好与变态倾向不独立

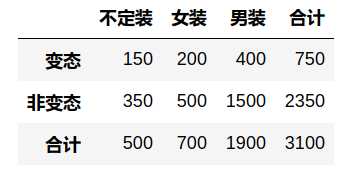
卡方检验一般需要先建立列联表，表中每个格子是观察频数，表示实际观测到的同时满足两个条件的数量：

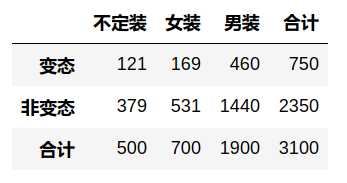
同时需要计算每个格子的期望频数，因为零假设是两个变量独立，因此依独立性的定义：$P(A,B) = P(A)\, P(B)$，于是上表中每个格子的期望频数为 $N \times P(A,B) = N \times P(A) \times P(B)$ ，其中 $N$ 为总数量，那么第一个格子的期望频数为 $3100 \times \frac{750}{3100} \times \frac{500}{3100} = 121$ 。因此总体期望频数表为：

有了这两个列联表后，就可以计算检验统计量 $\chi^2$ ( $\chi^2$ 表示卡方值) ，$\chi^2$ 越大，表示观测值和理论值相差越大，当 $\chi^2$ 大于某一个临界值时，就能获得统计显著性的结论：
\[ \chi^2 = \sum\frac{(观测频数 - 期望频数)^2}{期望频数}= \sum_{i=1}^{r} \sum_{j=1}^{c} {(O_{i,j} - E_{i,j})^2 \over E_{i,j}} \tag{1} \]

其中 $O_{ij}$ 为观测频数表中单元格的数值，$E_{ij}$ 为期望频数表中单元格的数值，$r$ 为行数，$c$ 为列数，自由度 $df$ 为 $(2-1)\times(3-1) = 2$ ，$\chi^2$ 服从卡方分布，则查卡方分布表：

得 $P(\chi^2 > 13.82) < 0.001$ ，而实际计算出的 $\chi^2$ 为 26.99，显著性很高，意味着零假设成立的情况下样本结果出现的概率小于 $0.1\%$，因而可以拒绝零假设，接受备选假设。这意味着男性的特殊着装偏好与变态倾向具有相关性。当然这里得说明两点：

本数据纯属虚构。
相关性不代表因果性，完全可能是第三个变量 (如：国籍) 同时导致了女装和变态，致使这两个变量产生了某种相关性。

再回到特征选择的问题，从严格的统计学角度来看，使用卡方检验进行特征选择可能会产生一些问题。假设选择的显著性水平 $\alpha$ 为 0.05，这说明犯第一类错误 ($\text{type} \, \text{I} \, \text{error}$，两个变量实际独立却被判为相关) 的概率为 5%，若进行了 1000 次卡方检验，则平均有 $1000 \times 0.05 = 50$ 次会选择与标签不相关的特征。机器学习问题中动辄就有几千至上百万的特征，那么这里面漏过的特征可能会相当多。不过好在搞机器学习并不是在搞统计，我们实际上比较关心的是特征的相对重要性。依上面的卡方分布表，检验统计量 $\chi^2$越大，越有信心拒绝零假设，接受两个变量不独立的事实，因而可以按每个特征 $\chi^2$ 值的大小进行排序，去除 $\chi^2$ 值小的特征。

以上就是卡方检验用于特征选择的一般流程，而我看到在大部分资料中举的例子都是离散型特征的，如下图：

这其中有几个值得注意的点：

(1) 上面举的卡方检验例子是判别 着装癖好与 变态倾向 具有相关性，然而 着装癖好 是离散型特征，而大部分机器学习模型是无法直接处理离散型特征的，如果按通常的作法进行 one-hot 转换 (如下图)，就不能确定其中单个的特征 (如 着装癖好_女装 ) 是否仍与 变态倾向 有相关性。

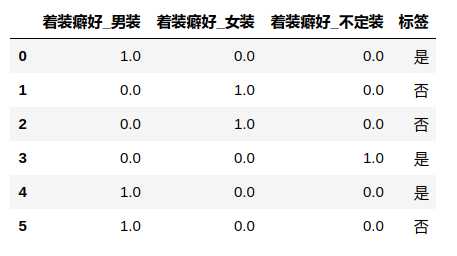
(2) 上面这一点也可以反过来看，假设卡方检验的结果是 着装癖好与 变态倾向 独立，也并不代表单个的特征 (如着装癖好_不定装 )与变态倾向 独立。所以综合这两点，应该先将离散型特征进行转换，再对每个特征进行卡方检验，而不是像这些资料中那样直接对一个离散型特征作检验。

(3) 如果是对 one-hot 转换后的每个特征构建列联表进行卡方检验，那将会是个巨大的工程，因为one-hot 转换通常会使特征维数成倍增加。因此我们需要一个快速计算 $\chi^2$ 的方法，而不是繁琐地对每个特征计算列联表频数，所幸 scikit-learn 中就提供了这样的快捷方法，同时也将看到这个方法也为连续型变量的应用打开了一扇大门。下面看 feature_selection.chi2 的源码 (有省略)：

def chi2(X, y):
    Y = LabelBinarizer().fit_transform(y)           # (1)
    if Y.shape[1] == 1:
        Y = np.append(1 - Y, Y, axis=1)
        
    observed = safe_sparse_dot(Y.T, X)              # (2)
    
    feature_count = X.sum(axis=0).reshape(1, -1)    # (3)
    class_prob = Y.mean(axis=0).reshape(1, -1)      # (4)
    expected = np.dot(class_prob.T, feature_count)  # (5)
    return _chisquare(observed, expected)

def _chisquare(f_obs, f_exp):
    f_obs = np.asarray(f_obs, dtype=np.float64)
    k = len(f_obs)
    
    chisq = f_obs
    chisq -= f_exp
    chisq **= 2
    with np.errstate(invalid="ignore"):
        chisq /= f_exp
    chisq = chisq.sum(axis=0)
    return chisq, special.chdtrc(k - 1, chisq)

这个实现并不是传统意义上的通过计算频数构建列联表，而是将属于每一个标签类别的特征取值总和作为列联表单元格的观测值，即第 (2) 步 (需要先在第 (1) 步将标签离散化)。而对于列联表单元格的期望值的计算，则是基于这样的假设：如果标签与特征独立，则每个标签类别为均匀分布，即第 (4) 步中的 $\rm{class\_prob} \Longrightarrow p$，则第 (5) 步中每个单元格期望值的计算就与传统意义上期望值类似了： $\mathbb{E}[x] = \sum_i p_i x_i$ 。接下来的_chisuqare() 方法则是按照公式 $(1)$ 计算 $\chi^2$ 值。

这样实现的一大好处是可以通过矩阵相乘快速得出所有特征的观测值和期望值，在计算出各特征的 $\chi^2$ 值后，如上文所述，可以按每个特征的 $\chi^2$ 值大小进行排序，方便地进行特征选择。另一个好处是扩大了 chi2 的适用范围，观察上面的代码，对于原始特征的唯一处理就是第 (3) 步中的 sum ，而不是原来的计算频数，这样一些连续型特征也可以使用该方法进行特征选择了。

F 检验

F 检验是一类建立在 F 分布基础上的假设检验方法，服从 F 分布的随机变量与上文中卡方分布的关系如下：

\[ F = \frac{X_1 / d_1}{X_2 / d_2} \tag{2} \]
其中 $X_1$ 和 $X_2$ 分别服从自由度为 $d_1$ 和 $d_2$ 的卡方分布，即 $X_1 \sim \chi^2(d_1), \;X_2 \sim \chi^2(d_2)$ ，且 $X_1$ 与 $X_2$ 独立，则随机变量 $F$ 服从自由度为 $(d_1, d_2)$ 的F分布，记为 $F \sim \text{F}(d_1, d_2)$ 。

下图显示不同自由度下F分布的概率密度曲线：

scikit-learn 中提供了两种F检验方法 —— 适用于分类的 f_classif 和适用于回归的 f_regression ，分别对应单因素方差分析和线性相关分析，下面分别介绍。

(1) 方差分析

在卡方检验中我们要测试的是被检验的特征与类别是否独立，若拒绝零假设，则特征与类别相关。而在方差分析中则采用了不同的思路：按照不同的标签类别将特征划分为不同的总体，我们想要检验的是不同总体之间均值是否相同 (或者是否有显著性差异)。下面承接上文的例子，类别为变态与否，因为方差分析只适用于连续型特征，所以这里采用了 “身高” 这个特征：

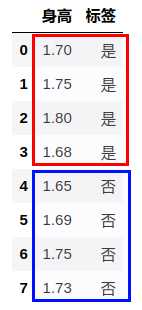
上图中红框和篮框中的特征值对应于两个类别区分出的两个不同的总体。方差分析用于特征选择的逻辑是这样：如果样本中是变态的平均身高为 1.7 米，非变态的平均身高也为 1.7 米，凭身高无法判定一个人变态与否，那么说明身高这个特征对于类别没有区分度，则可以去除。反之，若前者的平均身高为 1.6 米，后者的平均身高为 1.9 米，那么我们有理由认为身高很能区分变态与否。因此将问题形式化为假设检验问题：

零假设 ($H_0$)： $\mu_1 = \mu_2 = \cdots = \mu_k$ 备选假设 ($H_1$) ： $k$ 个总体的均值不全相等

下面阐述方差分析的原理。设共有 $k$ 个类别，总样本数为 $n$ ，第 $j$ 个类别的样本数为 $n_j$ ，$x_{ij}$ 表示第 $j$ 个类别的第 $i$ 个样本，$\bar{x_j}$ 表示第 $j$ 个类别的样本均值，即 $\bar{x_j} = \frac{\sum_{i=1}^{n_j} x_{ij}}{n_j}$ ，$\bar{x}$ 为总样本均值 $\bar{x} = \frac{\sum_{j=1}^k \sum_{i=1}^{n_j}x_{ij}}{n}$ ，那么样本的总体变异为：
\[ SST = \sum\limits_{j=1}^k \sum\limits_{i=1}^{n_j} (x_{ij} - \bar{x})^2 \]
$SST$ 可以分解为两部分 —— 类别内差异 $SSE$ 和类别间差异 $SSB$ ：
\[ \begin{array} & SSE = \sum\limits_{j=1}^k \sum\limits_{i=1}^{n_j} (x_{ij} - \bar{x_j})^2 \SSB = SST - SSE = \sum\limits_{j=1}^k n_j (\bar{x_j} - \bar{x})^2 \end{array} \]
$SSE$ 衡量每个类别内部样本之间的差异，可以认为是随机误差。$SSB$ 则衡量不同类别之间的差异。方差分析的基本思想是将不同类别之间的变异与随机误差作比较，如果二者之比大于某一临界值，则可拒绝零假设接受备选假设，即不同类别间样本均值不全相等，这也意味着样本特征对于类别有一定的区分度。

而对于如何确定临界值，则终于要用到传说中的 F 分布了。在 $(2)$ 式中已经定义了服从F分布的随机变量，注意到分子分母都要除以自由度，而 $SSE$ 和 $SSB$ 的自由度分别为 $k-1$ 和 $n-k$ ，因而统计检验量 $F$ ：
\[ F = \frac{类别间方差}{类别内方差} = \frac{MSB}{MSE} = \frac{SSB \,/\, (k-1)}{SSE\, / \, (n-k)} \]
服从分子自由度为 $k-1$，分母自由度为 $n-k$ 为的 F 分布，即 $\frac{MSB}{MSE} \sim F(k-1, \,n-k)$ 。看到这里，敏感的同学可能已经注意到了，方差分析的思想和线性判别分析 (Linear Discriminant Analysis，LDA) 非常类似 ( LDA 的思想可大致概括为 “投影后类内方差最小，类间方差最大”)。没错～，这两个方法都是由英国大统计学家和生物学家 Ronald Fisher 爵士所创立。

于是按假设检验的套路，零假设成立的情况下算出 F 值，查 F 分布表，若p值小于0.05 (或0.01)，则拒绝零假设接受备选假设，不同类别间均值不相等。在现实中使用软件包可以方便地输出方差分析表，这里使用 python 里的统计包 statsmodels：

import statsmodels
import statsmodels.api as sm
from statsmodels.formula.api import ols

lm = ols('标签 ~ 身高', data=data).fit()
table = sm.stats.anova_lm(lm, typ=1)
print(table)

#######################################################
           df    sum_sq   mean_sq         F     P(>F)
身高        1.0  0.188034  0.188034  0.622642  0.460102
Residual   6.0  1.811966  0.301994       NaN       NaN

从上表可以看出 $p$ 值为0.46，所以不能拒绝零假设，即身高这个特征无法区分变态与否。

方差分析可用于控制一个或多个自变量来检验其与因变量的关系，进而检测某种实验效果，因而与实验设计有着千丝万缕的关系，不过这里面的水颇深。。。甚至有很多专著，如《 Design and Analysis of Experiments 》等。就一般的特征选择问题而言，和卡方检验一样，我们依然比较关心的是特征的相对重要性，所以可以按每个特征 F 值的大小进行排序，去除F值小的特征。

上面的例子中检验身高与标签之间的关系，因为只有身高一个因素，所以被称为单因素方差分析。当然其他还有双因素方差分析，可以同时检验两个特征与标签的关系，以及两个特征之间的相互关系，缺点是计算繁琐，复杂度比单因素高。

单因素方差分析 (F检验) 与统计学中另一大假设检验方法 —— $t$ 检验也颇有渊源，检验统计量 F 与 t 检验中的检验统计量 t 的关系为： $F = t^2$ ，所以对于只有两个类别来说，F 检验和 t 检验会得出相同的结论，但对于多个类别的情况，t检验只能两两进行比较，这会带来一些问题：

多个类别之间两两比较，计算复杂度较高，如果有10个类别，则有 $C_{10}^2 = 45$ 种组合。
对原始资料的利用率低，每次只能用到全部实验数据的几分之一。
会增大假阳性 (即第一类错误) 的概率，假设显著性水平 $\alpha = 0.05$ ，则犯第一类错误的概率为0.05，那么不犯第一类错误的概率为 $1-0.05=0.95$。对于有5个类别，10个组合的两两比较问题，至少犯一次第一类错误的概率上升到 $1-0.95^{10} \approx 0.4$ ，这样就降低了统计推断的可靠性。

所以对于多个类别的比较，方差分析是首选，其相当于是 t 检验对于多类别的扩展，我想 scikit-learn 的特征选择模块中使用 F 检验而不是 t 检验是有这方面考虑的。

(2) 线性相关分析

对于特征和标签皆为连续值的回归问题，要检测二者的相关性，最直接的做法就是求相关系数 $r_{xy}$：
\[ r_{xy} = \frac{cov(x,y)}{\sigma_x \sigma_y} =\frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^n(x_i - \bar{x})^2} \sqrt{\sum_{i=1}^n (y_i - \bar{y})^2}} \]
但 scikit-learn 中的 f_regression 采用的是先计算相关系数，然后转化为F值。这又是个神奇的操作，究竟是如何转换的？在线性回归中常使用判定系数 $R^2$ 作为回归方程拟合数据点的程度，或者说是因变量的总体方差能被自变量解释的比例。$R^2$ 的定义以及和相关系数 $r_{xy}$ 的关系如下：
\[ R^2 = \frac{SSR}{SST} = 1- \frac{SSE}{SST} = r_{xy}^2 \]
其中 $SSE$ 为误差平方和：$SSE = \sum_{i=1}^n (y_i - \hat{y}_i)^2$ ，$SSR$ 为回归平方和：$SSR = \sum_{i=1}^n (\hat{y}_i - \bar{y})^2$ ，$SST$ 为总体平方和：$SST = \sum_{i=1}^n (y_i - \bar{y})^2$ 。可以看到这些式子与方差分析中的式子非常类似，不过注意这里计算的是都是标签值 $y$，而不是方差分析中的 $x$ 。这其中的原理都是相通的，我们同样可以用 $SSR$ 和 $SSE$ 来计算检验统计量 $F$ ($SSR$ 和 $SSE$ 的自由度分别为1和 n-2 )：
\[ F = \frac{MSR}{MSE} = \frac{SSR \,/\, 1}{SSE \,/\, (n-2)} = \frac{SSR / SST}{SSE / SST} \times (n-2) = \frac{r_{xy}^2}{1-r_{xy}^2} \times (n-2) \]
即 $\frac{MSR}{MSE} \sim F(1, \,n-2)$ 。这样就可以方便地将相关系数转化为 F 值了，接下来的步骤与之前的假设检验一样。该方法的缺点是只能检测线性相关关系，但不相关不代表独立，可能是非线性相关关系。

互信息

互信息 (mutual information) 用于特征选择，可以从两个角度进行解释：(1)、基于 KL 散度和 (2)、基于信息增益。对于离散型随机变量 $X, \,Y$，互信息的计算公式如下：
\[ I(X;Y) = \sum\limits_{y \in \mathcal{Y}}\sum\limits_{x \in \mathcal{X}} p(x,y) \,\text{log}\left(\frac{p(x,y)}{p(x)p(y)}\right) \tag{3.1} \]
对于连续型变量：
\[ I(X;Y) = \int_{\mathcal{Y}}\int_{\mathcal{X}} p(x,y) \,\text{log}\left(\frac{p(x,y)}{p(x)p(y)}\right) dxdy \tag{3.2} \]
可以看到连续型变量互信息的需要计算积分比较麻烦，通常先要进行离散化，所以这里主要讨论离散型变量的情况。互信息可以方便地转换为 KL 散度的形式：
\[ I(X;Y) = \sum\limits_{y \in \mathcal{Y}}\sum\limits_{x \in \mathcal{X}} p(x,y) \,\text{log}\left(\frac{p(x,y)}{p(x)p(y)}\right) = D_{KL}(p(x,y) || p(x)p(y)) \tag{3.3} \]
我们知道 KL 散度可以用来衡量两个概率分布之间的差异，而如果 $x$ 和 $y$ 是相互独立的随机变量，则 $p(x,y) = p(x)\,p(y)$ ，那么 $(3.3)$ 式为 $\huge{0}$。因此若 $I(X;Y)$ 越大，则表示两个变量相关性越大，于是就可以用互信息来筛选特征。

而从信息增益的角度来看，互信息表示由于 $X$ 的引入而使 $Y$ 的不确定性减少的量。信息增益越大，意味着特征 $X$ 包含的有助于将 $Y$ 分类的信息越多 (即 $Y$ 的不确定性越小)。决策树就是一个典型的应用例子，其学习的主要过程就是利用信息增益来选择最优划分特征，表示由于特征 $A$ 而使得对数据集 $D$ 的分类不确定性减少的程度，信息增益大的特征具有更强的分类能力。其计算公式为：
\[ \begin{align} I(D\,;A) & = H(D) - H(D|A) = H(D) - \sum\limits_{v=1}^\mathcal{V}\frac{|D^v|}{|D|} H(D^v) \tag{3.4} \& = -\sum\limits_{k=1}^\mathcal{K}\frac{|C_k|}{|D|}\,\text{log}\frac{|C_k|}{|D|} -\left(\sum\limits_{v=1}^\mathcal{V} \frac{|D^v|}{|D|}\sum\limits_{k=1}^\mathcal{K}\frac{|D_{k}^v|}{|D^v|}\,\text{log}\frac{|D_{k}^v|}{|D^v|}\right) \tag{3.5} \end{align} \]
$(3.4)$ 式中 $\mathcal{V}$ 表示特征 $A$ 有 $\mathcal{V}$ 个可能的取值，$|D^v|$ 表示第 $v$ 个取值上的样本数量。 $(3.5)$ 式中设总共有 $\mathcal{K}$ 个类别，$|C_k|$ 表示属于第 $k$ 类的样本数量，$\sum_{k=1}^\mathcal{K}|C_k| = |D|$。 $|D_k^v|$ 表示特征 $A$ 的取值为 $v$ 且类别为 $k$ 的样本数量。

互信息和信息增益，二者是等价的，下面我们来看表示互信息的 $(3.1)$ 式是如何推导出表示信息增益的 $(3.4)$ 和 $(3.5)$ 式的：
\[ \begin{align*} I(X;Y) = I(Y;X)&= \sum\limits_{y \in \mathcal{Y}}\sum\limits_{x \in \mathcal{X}} p(x,y) \,\text{log}\left(\frac{p(x,y)}{p(x)p(y)}\right) \& = -\sum\limits_y\sum\limits_x p(x,y)\,\text{log}\,p(y) + \sum\limits_x\sum\limits_y p(x,y)\text{log} \left(\frac{p(x,y)}{p(x)}\right) \& = -\sum\limits_y p(y)\,\text{log}\,p(y) + \sum\limits_x\sum\limits_y p(x)p(y|x)\text{log}\, p(y|x) \& = -\sum\limits_y p(y)\,\text{log}\,p(y) + \sum\limits_x p(x) \sum\limits_y p(y|x)\text{log}\, p(y|x) \tag{a} \& = H(Y) - \sum\limits_x p(x)H(Y|X=x) \tag{b}\& = H(Y) - H(Y|X) \end{align*} \]

上面的 $(a)$ 式就对应着 $(3.5)$ 式，而 $(b)$ 式对应 $(3.4)$ 式， $p(y) \simeq \frac{|C_k|}{|D|}\;,\; p(x) \simeq \frac{|D^v|}{|D|}\;,\; p(y|x) \simeq \frac{|D_{k}^v|}{|D^v|}$ 。由此可以看到决策树的学习过程也是一种依赖于训练数据的极大似然估计。

再来探究下 $(b)$ 式，$H(Y)$ 为熵，表示随机变量 $Y$ 的不确定性。$H(Y|X)=\sum\limits_{x}p(x) H(Y|X=x)$ 为条件熵 (conditional entropy)，表示在随机变量 $X$ 已知的情况下随机变量 $Y$ 的不确定性。那么二者的差 $I(X;Y) = H(Y) - H(Y|X)$ 就表示由于 $X$ 的引入而使 $Y$ 的不确定性减少的量，维基里有一张形象的图：

放在特征选择的语境下，我们希望 $Y$ 的不确定越小越好，这样越有助于分类，那么互信息越大，则特征 $X$ 使得 $Y$ 的不确定性减少地也越多，即 $X$ 中包含的关于 $Y$ 的信息越多。因而策略还是和上文一样，计算每个特征与类别的互信息值，排序后去除互信息小的特征。

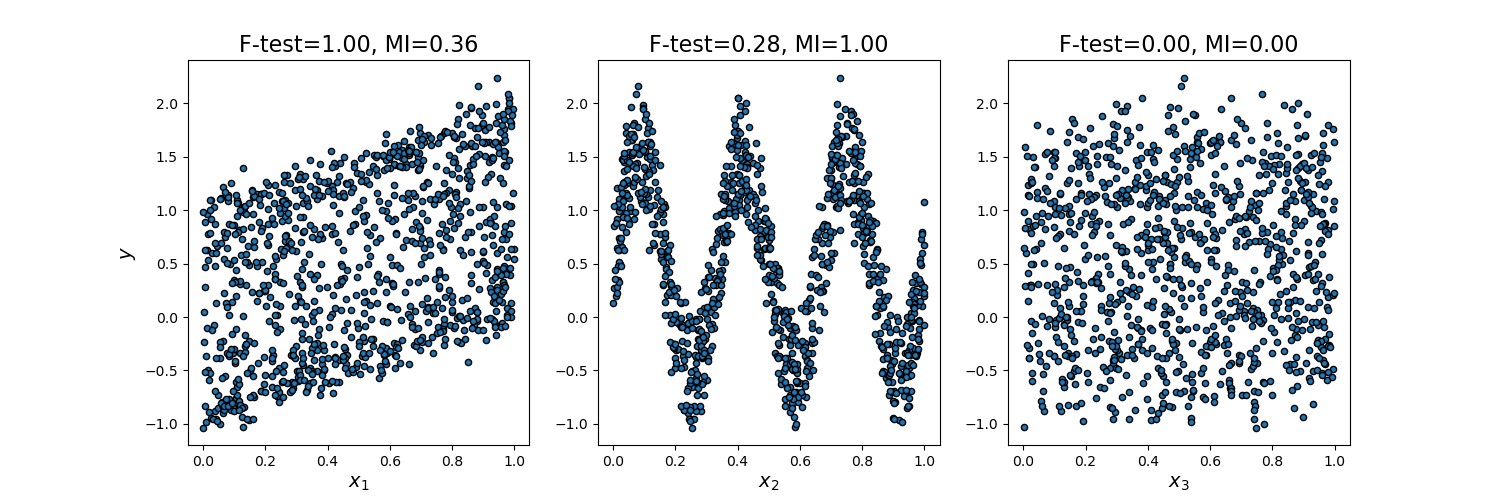
互信息的一大优点是其能检测出多种变量之间的关系，而相较而言 F 检验只能表示线性相关关系。Scikit-learn 的这个例子 (Comparison of F-test and mutual information) 中显示了这一点，互信息能很好展现 $x$ 和 $y$ 之间的非线性关系：