标签:color 复杂 false 网络 example 技术 init ESS get
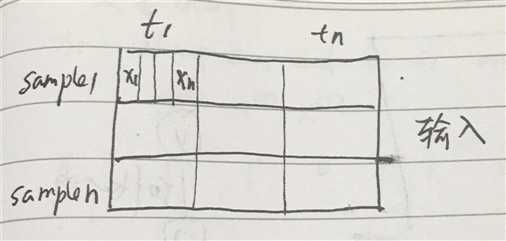
基础的LSTM模型,单隐层,隐层单神经元,而实际中一般需要更为复杂的网络结构,
下面借用手写数字的经典案例构造比较复杂的LSTM模型,并用代码实现。
单隐层,隐层多神经元
# -*- coding:utf-8 -*- import tensorflow as tf from tensorflow.examples.tutorials.mnist import input_data # 导入数据 mnist = input_data.read_data_sets(‘MNIST_data‘,one_hot = True) training_iters = 50001 batch_size = 100 # 批量大小 n_inputs = 28 n_steps = 28 # 序列长度 n_hidden_number = 128 # 隐藏层神经元个数 n_outputs = 10 # 输出层神经元个数 x = tf.placeholder(tf.float32,[None,n_steps,n_inputs]) # 输入3维 样本数*序列长度*每个元素长度 Y = tf.placeholder(tf.float32,[None,n_outputs]) weights = { # 权重设定同全连接,这是单步权重 # 每步权重共享 # shape = (28,128) ‘in‘:tf.Variable(tf.random_normal([n_inputs,n_hidden_number])), # shape = (128,10) ‘out‘:tf.Variable(tf.random_normal([n_hidden_number,n_outputs]))} biases = { # shape = (128,) ‘in‘:tf.Variable(tf.constant(0.1,shape = [n_hidden_number,])), # shape = (10,) ‘out‘:tf.Variable(tf.constant(0.1,shape = [n_outputs,]))} def RNN(X,weights,biases): """ 这里是整个RNN的网络 1. 输入x是整个序列的,即 [x1,x2,..xt]*samples 2. 隐层的输出包含了序列中每个时间的输出 """ ### 输入层到核运算 ### # X shape = (100batch,28steps,28inputs) ==> (100batch*28steps,28inputs) X = tf.reshape(X,[-1,n_inputs]) # 之所以转成2维,是要与weight相乘 # X_in shape ==> (100batch*28steps,128hidden) X_in = tf.matmul(X,weights[‘in‘])+biases[‘in‘] # 这是所有样本每个时序都乘以weight,每个时序都变成了hidden_num长度,结果是所有样本每个时序的hidden_num长,此时所有样本混在一起 # X_in shape ==> (100batch,28steps,128hidden) # 然后要重新划分成样本,每个样本有n_steps个时序,每个时序是hidden_num长,按样本送给隐层 X_in = tf.reshape(X_in,[-1,n_steps,n_hidden_number]) ### cell核内运算 ### ## 构建纵向rnn网络,单隐层,n_hidden_number个神经元 lstm_cell = tf.nn.rnn_cell.BasicLSTMCell(n_hidden_number,forget_bias = 1.0) # LSTM cell is divided into two parts-->(c_state,m_state) # 初始化s init_state = lstm_cell.zero_state(batch_size,dtype=tf.float32) ## 构建横向rnn网络 # outputs states 都是隐层的输出,整个RNN所有时序的输出,但只是h,还没到o o=vh+c(c是bias,不同于states的c,这是记忆单元) # outputs 是以三维矩阵的形式记录了所有样本所有时序的所有隐层神经元的输出,shape为[batch_size, timestep_size, hidden_size] # states 是最后时刻的c 和 h,c是记忆,shape为 [batch_size, 2, hidden_size] # 当然通常顺序是这样的[2, batch_size, hidden_size] outputs,states = tf.nn.dynamic_rnn(lstm_cell,X_in,initial_state=init_state,time_major=False) ### 核内运算到输出层 ### # states[1]就是所有样本最后时刻的h, 实际上 states[1] == outputs[:,-1,:] result = tf.matmul(states[1],weights[‘out‘])+biases[‘out‘] # result就是o return result prediction = RNN(x,weights,biases) ### 后面所有的神经网络都大同小异 loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=Y, logits=prediction)) train_step = tf.train.AdamOptimizer(1e-3).minimize(loss) correct_prediction = tf.equal(tf.argmax(prediction,1), tf.argmax(Y,1)) accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) init = tf.global_variables_initializer() with tf.Session() as sess: sess.run(init) step = 0 while step*batch_size < training_iters: batch_xs,batch_ys = mnist.train.next_batch(batch_size) # batch_xs shape = [100,28,28] batch_xs = batch_xs.reshape([batch_size,n_steps,n_inputs]) train_step.run(feed_dict={x:batch_xs,Y:batch_ys,}) if step%50 == 0: train_accuracy = accuracy.eval(feed_dict={x:batch_xs,Y:batch_ys,}) print("step", step, "training accuracy", train_accuracy) step += 1
上面的网络大概是这样
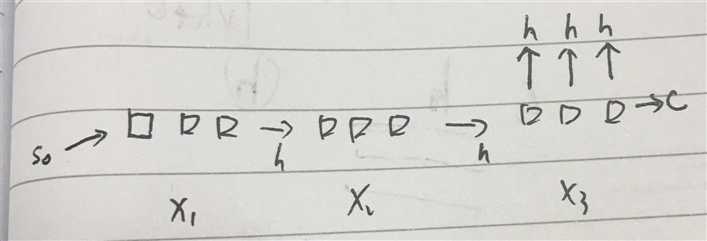
x1 x2 其实应该是 xt1 xt2
多层隐层,隐层多节点
layer_num = 2 # 隐层数
def clstm():
lstm_cell = tf.nn.rnn_cell.BasicLSTMCell(num_units=hidden_size, forget_bias=1.0, state_is_tuple=True)
lstm_cell = rnn.DropoutWrapper(cell=lstm_cell, input_keep_prob=1.0, output_keep_prob=keep_prob)
return lstm_cell
# 调用 MultiRNNCell 来实现多层 LSTM
mlstm_cell = rnn.MultiRNNCell([clstm() for i in range(layer_num)], state_is_tuple=True)
init_state = mlstm_cell.zero_state(batch_size, dtype=tf.float32)
outputs, state = tf.nn.dynamic_rnn(mlstm_cell, inputs=X, initial_state=init_state, time_major=False)
h_state = outputs[:, -1, :]
其他代码雷同
标签:color 复杂 false 网络 example 技术 init ESS get
原文地址:https://www.cnblogs.com/yanshw/p/10496290.html