标签：进制   修改   img   inf   相关   快速幂   ase   image   size   

快速幂

快速幂其实就是“翻倍”相乘，比如，要算5^15，我们可以这样拆开：5^( 1 + 2 + 4 + 8 )，变成 (5^1) * (5^2) * (5^4) * (5^8)。计算5^2时，就是把5^1“翻倍”，也就是算(5^1)^2；计算5^4时，就是把5^2翻倍，也就是算(5^2)^2；计算5^8时同理可得。所以，代码就是：

int base = 5;
int res = 1;
for(int i = 1; i <= 4; i++){
    res = res * base;
    base = base * base;
}

但是，如果幂没有这么特殊，假如算5^10，那这个怎么办？我们回过头来看5^15这个例子，我们看到：1，2，4，8 ----- 这些数都是2的幂次（当然是2的幂次啦，不是2的幂次怎么“翻倍”）。显然，这些数加起来是15（ 废话(￣▽￣)" ）。那么，我们怎样选，才能选出一组是2的幂次的数（这里就是1,2,4,8），而且加起来是等于幂（这里的幂就是15）。答案就在于二进制。我们把15转化成二进制就是：

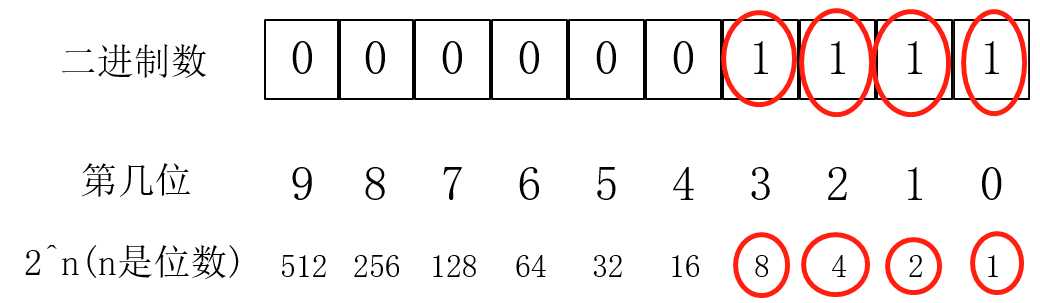
其实就是15 == 1*(2^0) + 1*(2^1) + 1*(2^2) + 1*(2^3) == 1*1+1*2+1*4+1*8。同理，对于5^10的幂（就是10），我们转化为二进制后，就是这样：

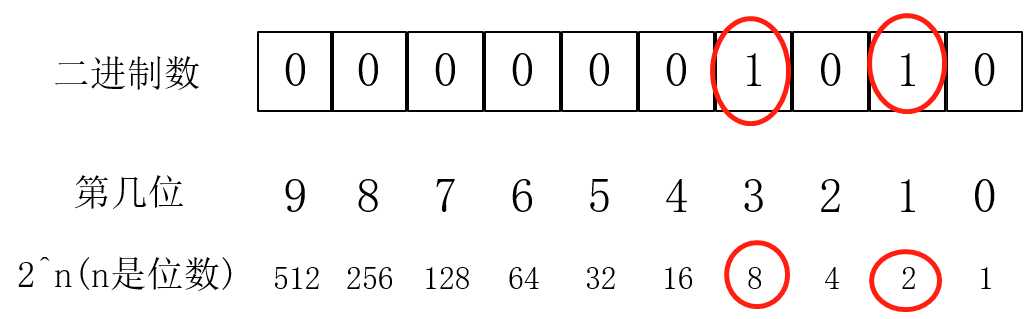
其实就是10 == 0*(2^0) + 1*(2^1) + 0*(2^2) + 1*(2^3) == 0*1+1*2+0*4+1*8。二进制帮助了我们对于2的幂次的数（也可以称为公比为2，首项为1的等比数列，其实也就是1,2,4,8,16,32.......）的选择：选（对应的二进制数位为1）和不选（对应的二进制数位为0）。对于15，就是这个样子的：1,2,4,8都选，对于10，只选2,8，不选1,4。这样弄有什么好处呢？我们直接来看代码：

1 //快速幂模板
2 int base = 5;  //base:底数
3 int m = 10;    //m:幂
4 int res = 1    //res:结果
5 while(m){
6     if(m % 2 == 1) res = res * base;  
7     base = base * base;    
8     m = m / 2;
9 }

首先，我们看看第7行代码：其实就是翻倍，得到base^1，base^2，base^4，base^8......。对于第6行的代码，我想有人大概猜到了是什么作用：如果当前二进制位是1，那么就乘上base，否则不乘入结果。对应我们的5^10来说，就是res = (base^2)*(base^8)（上面提到了对于10只选2,8）。那么，我们怎样取出10的二进制位？对于二进制的位是0时，只要判断数的奇偶，就可以判断0位的二进制是0还是1：

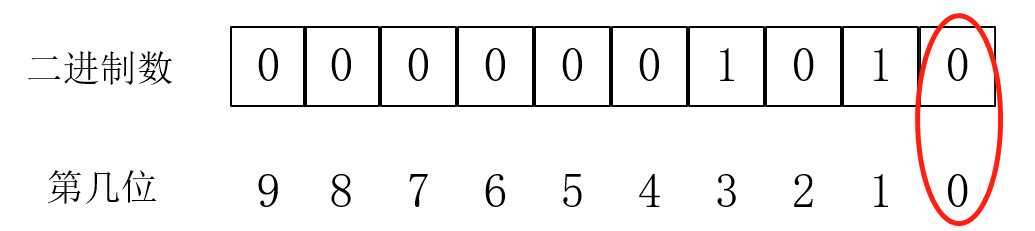
对于二进制的位是1的时候：

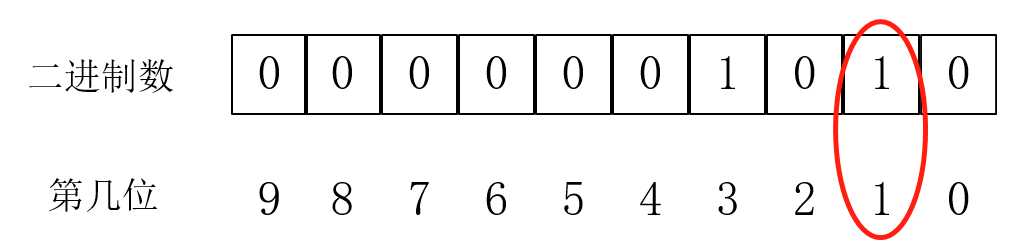
我们只需要把二进制数向右移一位，也就是这样：

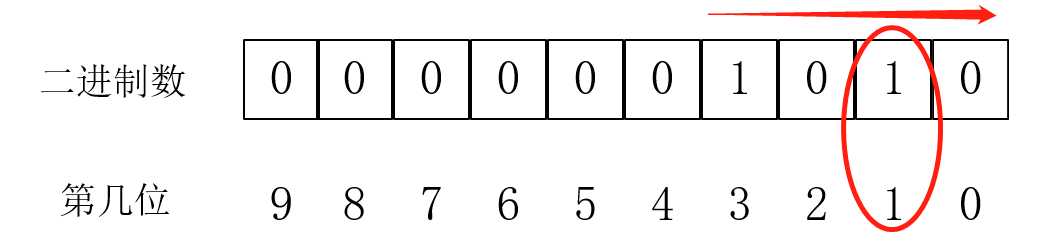
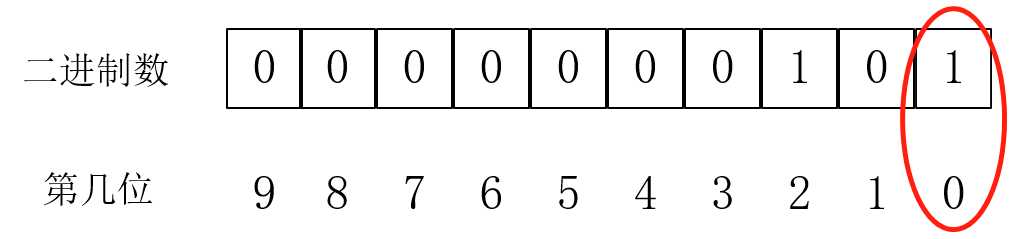
这时，之前二进制的1位变成了二进制的0位。我们只需要按照之前的方法就可以判断这个位到底选不选。右移一位的操作：第8行代码，就是直接除2。呃，解释的话，就是向右移一位时，因为所有的位都要向右一位，而一位的大小是2，所以要除于2，这跟把一个十进制的数里面的每个位取出来的道理是一样的。经过更形象的修改，我们还可以把代码改成这样：

1 //快速幂模板
2 int base = 5;  //base:底数
3 int m = 10;    //m:幂
4 int res = 1    //res:结果
5 while(m){
6     if(m & 1) res *= base;  
7     base *= base;    
8     m >>= 1;
9 }

如何判断幂的二进制位全部取出来？当幂被右移变成0时就说明没有位可取了，就是第5行代码。

不懂的话可以直接复制以上模板。

暂更。

数论，组合数学相关

标签：进制   修改   img   inf   相关   快速幂   ase   image   size   

原文地址：https://www.cnblogs.com/happy-MEdge/p/10503565.html