标签:alt c代码 can ast lin 执行命令 cas return uva
https://vjudge.net/problem/UVA-1622
有一个 $n\times m$ ($1\leqslant n,m\leqslant10^5$)的网格,每个格子里都有一个机器人,每次可以发出以下4种指令之一:NORTH、SOUTH、EAST、WEST,作用是让所有机器人往相应方向走一格。如果一个机器人在执行某一命令后走出了网格,则它会立即炸毁。
给出4种指令的总条数($0\leqslant C_N,C_S,C_W,C_E\leqslant 10^5$),求一种指令顺序使得所有机器人执行的命令条数之和最大。炸毁的机器人不再执行命令。
神题……虽然看起来很简单,但细节一大堆
尝试从网上搜索题解,但貌似都有点问题……
想了三天,只说下策略了……
首先处理数据,让$N\leqslant S$且$W\leqslant E$,第一次考虑是东西来回还是南北来回
一开始就来回肯定比后面来回更优
先S再N肯定比先N再S更优,因为如果先执行N会比先执行S少用一次S,多出来的S会在后面执行,能执行这条指令的机器人肯定比现在少。
同理可得先E后W
第一个到底是选东西来回还是南北来回可以推公式(不敢推= =),也可以都算一遍,得到最后结果以后取最大
因为可以通过交换得到,因此我们选东西来回,于是只剩下东和南北
选了以后就进行下图这种选择
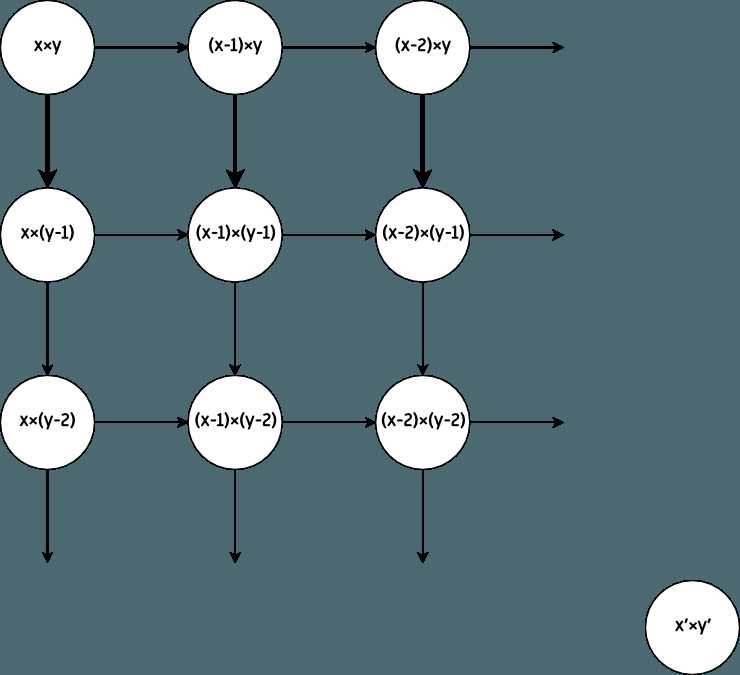
粗箭头表示南北来回
目标是从$x\times y$走到$x‘\times y‘$的和最大
虽然可以直接模拟出所有情况,但看到这题$1\leqslant n,m\leqslant10^5$感觉$O(n^2)$很悬……不敢写
现在把问题分解成几个
1.第一行每个位置向下移动包含了多少面积(左闭右开,方便加)
2.从$x\times y$走到$x‘\times y‘$(不经过粗箭头)的和最大是多少
3.从第一行什么位置向下最优
3可以$O(n)$得出,1和2只能用$O(1)$了
1直接推公式就好了……
2也是推公式,虽然比较麻烦
可以证明尽量往正方形走最好(减少长边),因为如果减少短边损失更大,并且后面补不回来了
因此可以分成两种情况
2.1起始点和目标点都在y=x的一侧

可以把右边那种情况通过交换x,y(关于y=x对称)得到左边那种
易得
\[S=\frac{{xy + x‘y}}{2} \times \left( {x - x‘ + 1} \right) - x‘y + \frac{{x‘y + x‘y‘}}{2} \times \left( {y - y‘ + 1} \right) - x‘y‘\]
2.2起始点和目标点在y=x的两侧(上)
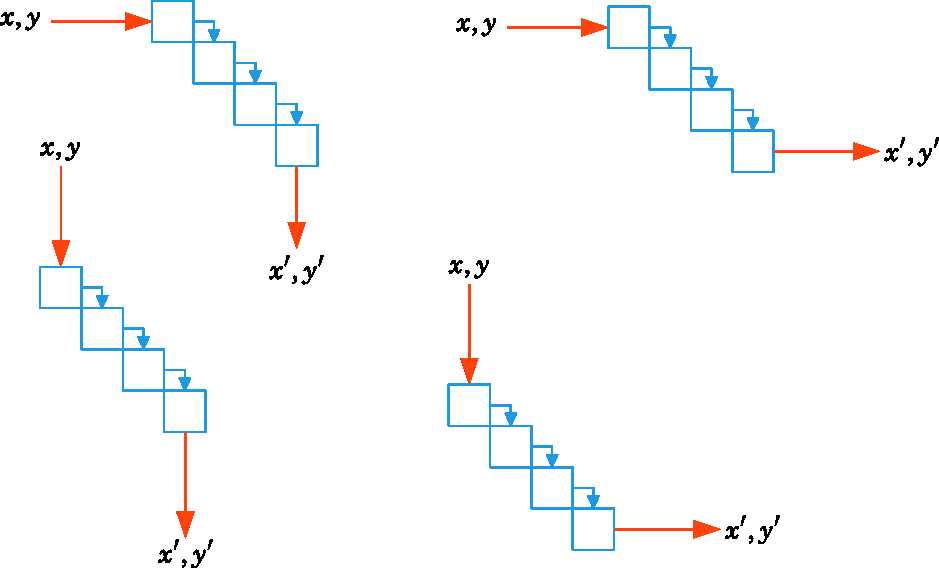
需要用平方和公式
\[\sum\limits_{i = 1}^n {{i^2}} = \frac{{n\left( {n + 1} \right)\left( {2n + 1} \right)}}{6}\]
为了简洁,设:
\[M_1=\max\{x,y\}, m_1=\min\{x,y\}\]
\[M_2=\max\{x‘,y‘\}, m_2=\min\{x‘,y‘\}\]
易得
\[S=S_1+S_2+S_3\]
\[S_1=\frac{{xy + m_1^2}}{2} \times \left( {{M_1} - {m_1} + 1} \right) - m_1^2\]
\[S_3 = \frac{{x‘y‘ + M_2^2}}{2} \times \left( {{M_2} - {m_2} + 1} \right) - x‘y‘\]
\[{S_2} = \left[ {\frac{{{m_1}\left( {{m_1} + 1} \right)\left( {2{m_1} + 1} \right)}}{6} - \frac{{{M_2}\left( {{M_2} + 1} \right)\left( {2{M_2} + 1} \right)}}{6}} \right] \times 2 - \left( {\frac{{{m_1} + {M_2}}}{2} \times \left( {{M_2} - {m_1} + 1} \right) - {M_2}} \right)\]
如何判断在两侧呢,这可以用向量外积……
还要注意某一方向不移动的情况(不知道为什么会变成特例= =,面向样例和对拍程序的编程)
时间复杂度$O(n)$
AC代码:
#pragma GCC optimize("Ofast,no-stack-protector,unroll-loops,fast-math")
#include<bits/stdc++.h>
using namespace std;
#define REP(r,x,y) for(register int r=(x); r<(y); r++)
#define REPE(r,x,y) for(register int r=(x); r<=(y); r++)
#ifdef sahdsg
#define DBG(...) printf(__VA_ARGS__)
#else
#define DBG(...)
#endif
typedef long long LL;
inline bool lc(LL x, LL y, LL x_, LL y_) {
LL vect1z = y_-x; //(1,1)X(x,y_)
if(vect1z<0) vect1z=-1;
else if(vect1z==0) vect1z=0;
else if(vect1z>0) vect1z=1;
LL vect2z = y-x_; //(1,1)X(x_,y)
if(vect2z<0) vect2z=-1;
else if(vect2z==0) vect2z=0;
else if(vect2z>0) vect2z=1;
return vect1z*vect2z<=0;
}
inline LL get1(LL x, LL y, LL x_, LL y_) {
if(y>x) {
swap(x,y), swap(x_,y_);
}
LL _1 = (x*y+x_*y)*(x-x_+1)/2 - x_*y + (x_*y+x_*y_)*(y-y_+1)/2 - x_*y_;
return _1;
}
inline LL get2(LL x, LL y, LL x_, LL y_) {
LL M1 = max(x,y), m1 = min(x,y);
LL M2 = max(x_,y_), m2 = min(x_,y_);
LL _1 = (x*y+m1*m1)*(M1-m1+1)/2-m1*m1;
LL _3 = (x_*y_+M2*M2)*(M2-m2+1)/2-x_*y_;
LL _2 = ((m1*(m1+1)*(2*m1+1))/6-(M2*(M2+1)*(2*M2+1))/6)*2 -((m1+M2)*(m1-M2+1)/2-M2);
return _1+_2+_3;
}
inline LL get4(LL x, LL y, LL x_, LL y_) {
x_ = max(0LL,x_), y_ = max(0LL,y_);
if(lc(x,y,x_,y_)) {
return get2(x,y,x_,y_);
}else{
return get1(x,y,x_,y_);
}
}
inline LL getWE(LL &x, LL &y, LL &E, LL &W) {
LL _1 = 2*W * (x-1)*y+y;
E-=W, x--;
if(E) _1 += x*y,E--;
return _1;
}
inline LL getNS(LL &x, LL &y, LL &S, LL &N) {
LL _1 = 2*N * x*(y-1)+x;
S-=N, y--;
if(S) _1 += x*y,S--;
return _1;
}
LL n,m,N,S,W,E;
inline LL solve(LL n, LL m, LL N, LL S, LL W, LL E) {
LL ans=0;
if(S<N) swap(S,N);
if(E<W) swap(E,W);
if(m>1) {
if(W>0) {
ans+=getWE(m,n,E,W);
} else if(E>0) {
ans+=m*n, E--, m--;
}
}
LL mx=-1;
LL _2=ans;
E = min(E,m);
while(E>=0) {
LL _m=m, _n=n, _S=S, _N=N;
LL _1=_2;
if(_n>1)_1+=getNS(_m,_n,_S,_N);
_1+=get4(_m,_n,_m-E,_n-_S);
mx = max(mx,_1);
_2+=m*n;
E--,m--;
}
return mx;
}
inline LL solve2(LL n, LL m, LL W, LL E) {
LL ans=0;
if(S<N) swap(S,N);
if(E<W) swap(E,W);
if(m>1) {
if(W>0) {
ans+=getWE(m,n,E,W);
} else if(E>0) {
ans+=m*n, E--, m--;
}
}
E = min(E,m);
ans+=get4(m,n,m-E,n);
return ans;
}
int main() {
#ifdef sahdsg
// freopen("in.txt", "r", stdin);
#endif
int kase = 0;
while(~scanf("%lld%lld", &n, &m) && n) {
kase++;
scanf("%lld%lld%lld%lld", &N, &S, &W, &E);
if(N||S||W||E) {
if(N+S && W+E)
printf("Case %d: %lld\n", kase, max(
solve(n,m,N,S,W,E),
solve(m,n,W,E,N,S)
)
);
else {
if(N+S) {
printf("Case %d: %lld\n", kase, solve2(m,n,N,S));
} else {
printf("Case %d: %lld\n", kase, solve2(n,m,W,E));
}
}
} else
printf("Case %d: 0\n", kase);
}
return 0;
}
AC后真的激动得哭
标签:alt c代码 can ast lin 执行命令 cas return uva
原文地址:https://www.cnblogs.com/sahdsg/p/10538739.html