标签:RoCE 接受 最优 函数 int assert array png arch
目录
在介绍下降方法之前,我们需要先看一些预备的知识。
我们假设目标函数在下水平集\(S\)上是强凸的,这是指存在\(m > 0\),使得
\[
\nabla^2 f(x) \succeq mI
\]
对于任意\(x\)成立。
注意,这个广义不等式,是指\(\nabla^2 f(x) - mI\)半正定,即,\(\nabla^2 f(x)\)的最小特征值大于等于\(m\)。
对于\(x, y\in S\),我们有广义泰勒展开:
\[
f(y)=f(x)+\nabla^{T}(y-x)+\frac{1}{2}(y-x)^{T}\nabla^{2}f(z)(y-x)
\]
\(z \in [x,y]\)
利用强凸性假设,可以推得不等式(同时可知,\(S\)是有界的):
\[
f(y) \ge f(x) + \nabla f(x)^{T}(y-x) + \frac{m}{2}\|y-x\|_2^2
\]
通过,不等式右边是关于\(y\)的二次凸函数,令其关于\(y\)的导数等于零,可以得到该二次函数的最优解\(\widetilde{y} = x-(1/m)\nabla f(x)\),所以
\[
f(y) \ge f(x) - \frac{1}{2m}\|\nabla f(x)\|_2^2
\]
\(x^*\)是\(f(x)\)的全局最优解,\(p^*=f(x^*)\),因为上述不等式对于任意\(y\)都成立,所以:
\[
p^* \ge f(x) - \frac{1}{2m} \|\nabla f(x)\|_2^2
\]
由此可见,任何梯度足够小的点都是近似最优解。由于,
\[
\|\nabla f(x)\|_2 \le (2m\epsilon)^{1/2} \Rightarrow f(x) - p^* \le \epsilon
\]
我们可以将其解释为次优性条件。
因为\(S\)有界,而\(\nabla^2 f(x)\)的最大特征值是\(x\)在\(S\)上的连续函数,所以它在\(S\)上有界,即存在常数\(M\)使得:
\[
\nabla^2 f(x) \preceq MI
\]
关于Hessian矩阵的这个上界,意味着,对任意的\(x, y \in S\):
\[
f(y) \le f(x) + \nabla f(x)^T(y-x) + \frac{M}{2} \|y-x\|_2^2
\]
同样,可以得到:
\[
p^* \le f(x) - \frac{1}{2M} \|\nabla f(x)\|_2^2
\]
注意:
\[
mI \preceq \nabla^2 f(x) \preceq MI
\]
\(\kappa = M/m\)为矩阵\(\nabla^2 f(x)\)的条件数的上界。通常,\(\kappa\)越小(越接近1),梯度下降收敛的越快。这个条件会在收敛性分析中反复用到。
由凸性知:\(\nabla f(x^{(k)})^T (y-x^{(k)}) \ge 0\)意味着\(f(y) \ge f(x^{(k)})\),因此一个下降方法中的搜索方向必须满足:
\[
\nabla f(x^{(k)})^T \Delta x^{(k)} < 0
\]
我们并没有限定下降方向\(\Delta x\)必须为逆梯度方向,事实上这种选择也仅仅是局部最优的策略。
所以算法是如此的:

停止准则通常根据次优性条件,采用\(\|\nabla f(x)\| \le \eta\),其中\(\eta\)是小正数。
梯度下降方法的算法如下:

精确直线搜索需要我们求解下面的单元的优化问题:
\[
t = argmin_{s \ge 0} f(x+s \Delta x)
\]
因为问题是一元的,所以相对来说比较简单,可以通过一定的方法来求解该问题,特殊情况下,可以用解析方法来确定其最优解。
在收敛性分析的时候,我们选择\(\Delta x := -\nabla f(x)\)。
我们定义:\(\widetilde{f}(t)=f(x-t\nabla f(x))\),同时,我们只考虑满足\(x-t\nabla f(x) \in S\)的\(t\)。通过预备知识,我们容易得到下面的一个上界:
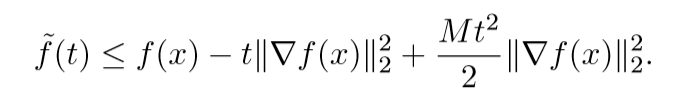
对上述不等式俩边同时关于\(t\)求最小,左边等于\(\widetilde{f}(t_{exact})\),右边是一个简单的二次型函数,其最小解为\(t=1/M\),因此我们有:
\[
f(x^{+}) = \widetilde{f}(t_{exact}) \le f(x) - \frac{1}{M} \|\nabla(f(x))\|_2^2
\]
从该式俩边同时减去\(p^*\),我们得到
\[
f(x^+)-p^* \le f(x) - p^* - \frac{1}{M} \|\nabla f(x)\|_2^2
\]
又\(\|\nabla f(x)\|_2^2 \ge 2m(f(x)-p^*)\),可以断定:
\[
f(x^+) -p ^* \le (1-m/M)(f(x)-p^*)
\]
重复进行,可以看出,
\[
f(x^+) -p ^* \le (1-m/M)^{k}(f(x)-p^*)
\]
收敛性分析到这为止,更多内容翻看凸优化。
回溯直线搜索,不要求每次都减少最多,只是要求减少足够量就可以了。其算法如下:

回溯搜索从单位步长开始,按比例逐渐减少,直到满足停止条件\(f(x+t\Delta x) \le f(x) + \alpha t \nabla f(x)^T \Delta x\)。
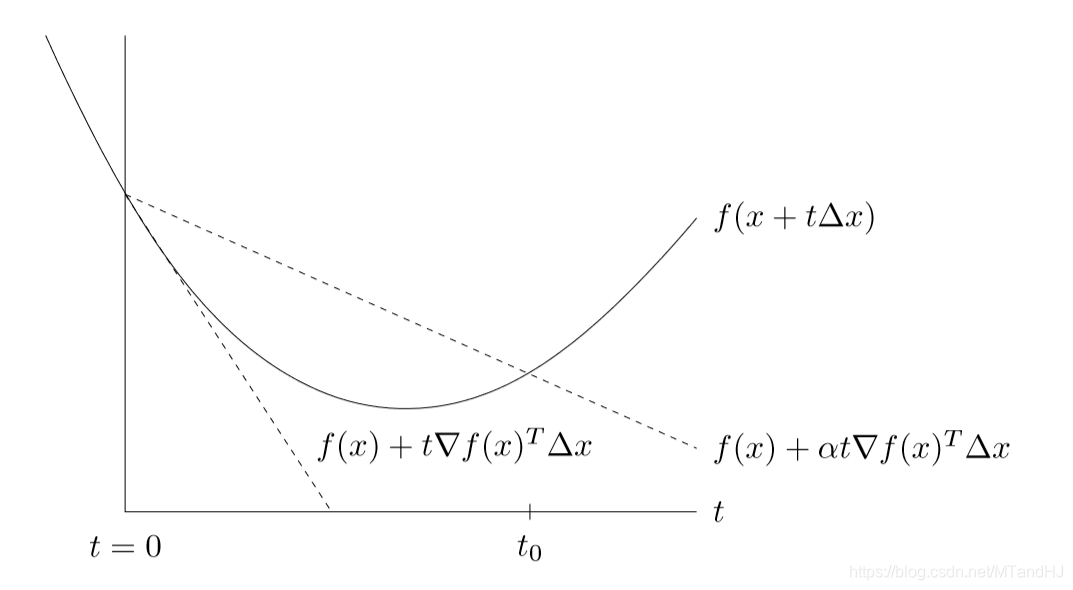
最后的结果\(t\)满足\(t \ge min\{1, \beta t_0 \}\)。
在实际计算中,我们首先用\(\beta\)乘\(t\)直到\(x+t\Delta x \in dom f\),然后才开始检验停止准则是否成立。
参数\(\alpha\)的正常取值在0.01 和 0.3 之间表示我们可以接受的\(f\)的减少量在基于线性外推预测的减少量的\(1\%\)和\(1\%\)之间。参数\(\beta\)的正常取值在 0.1(对应非常粗糙的搜索)和 0.8(对应于不太粗糙的搜索)之间。
我们先证明,只要\(0 \le t \le 1/M\),就能满足回溯停止条件:
\[
\widetilde{f}(t) \le f(x) - \alpha t \|\nabla f(x)\|
\]
首先,注意到:
\[
0 \le t \le 1/M \Rightarrow -t + \frac{Mt^2}{2} \le -t/2
\]
由于\(\alpha < 1/2\)(这也是为什么我们限定\(\alpha < 1/2\)的原因),所以可以得到:
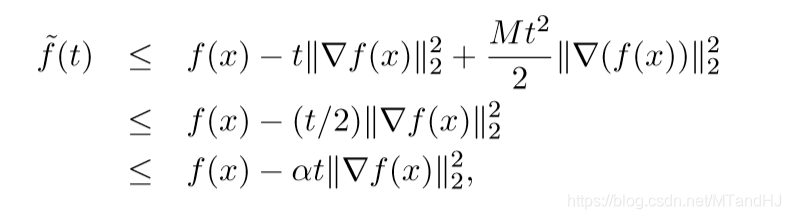
因此,回溯直线搜索将终止于\(t=1\)或者\(t\ge \beta/M\)。故:
\[
f(x^+) \le f(x) - \min \{\alpha, (\beta \alpha / M) \} \|\nabla f(x)\|_2^2
\]
俩边减去\(p^*\),再结合\(\|\nabla f(x)\|_2^2 \ge 2m(f(x)-p^*)\)可导出:
\[
f(x^+)-p^* \le (1-\min \{2m\alpha, 2 \beta \alpha m/M \})^{k}(f(x) - p^*)
\]
我们选取初始点为\((\gamma, 1),\gamma=10\)
下图是精确直线搜索:
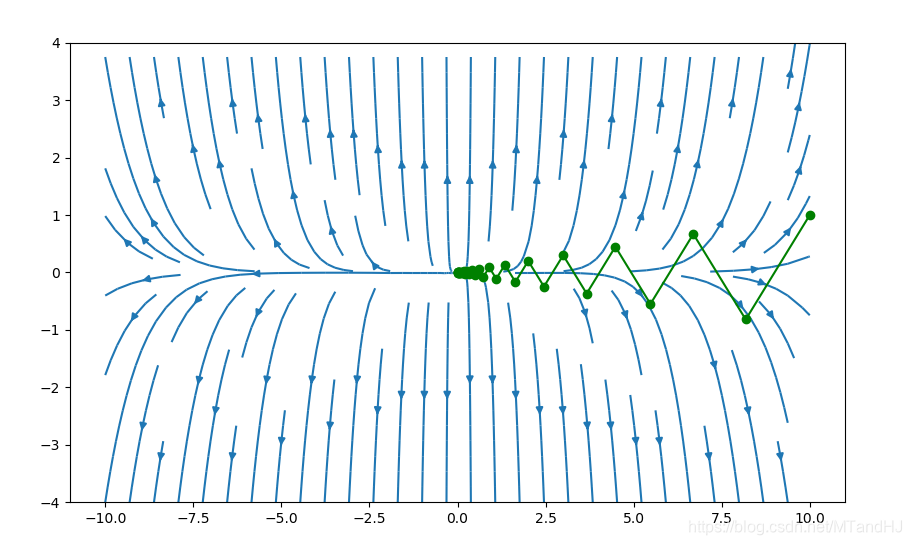
下图是回溯直线搜索,\(\alpha=0.4, \beta=0.7\)可以看出来,每一次的震荡的幅度比上面的要大一些。
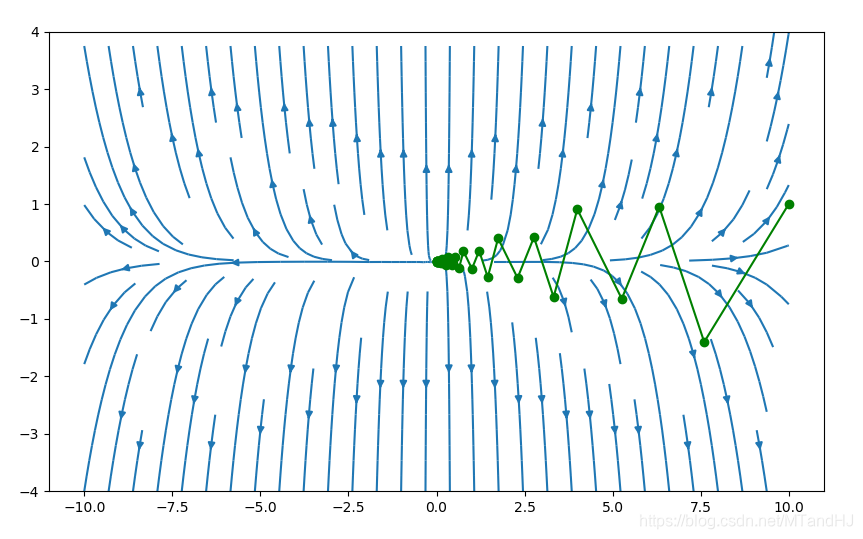
下面采用的是回溯直线搜索,\(\alpha=0.4,\beta=0.7\),初始点为\((7,3)\)
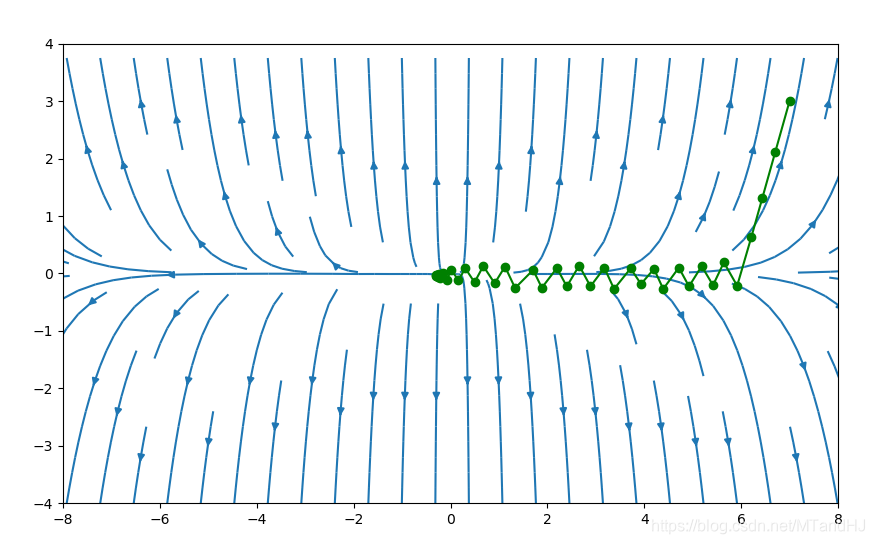
初始点为\((-7, -3)\)
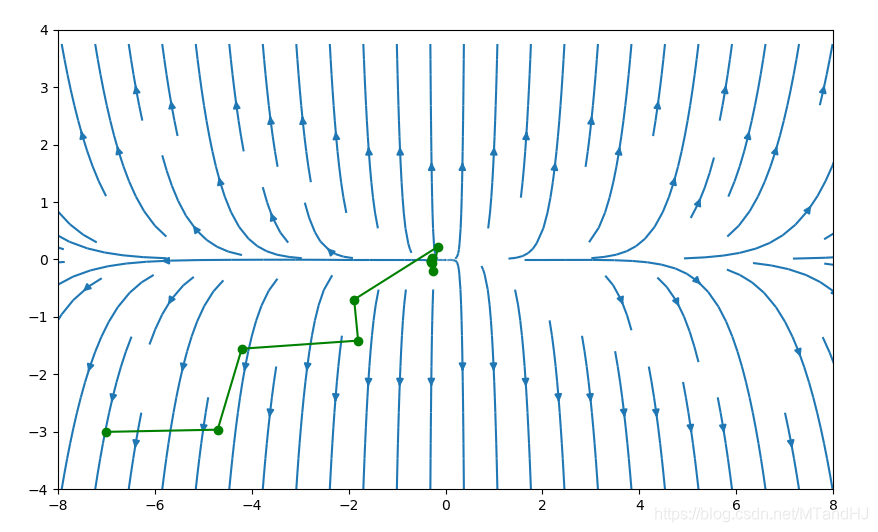
\(\alpha=0.2,\beta=0.7\)
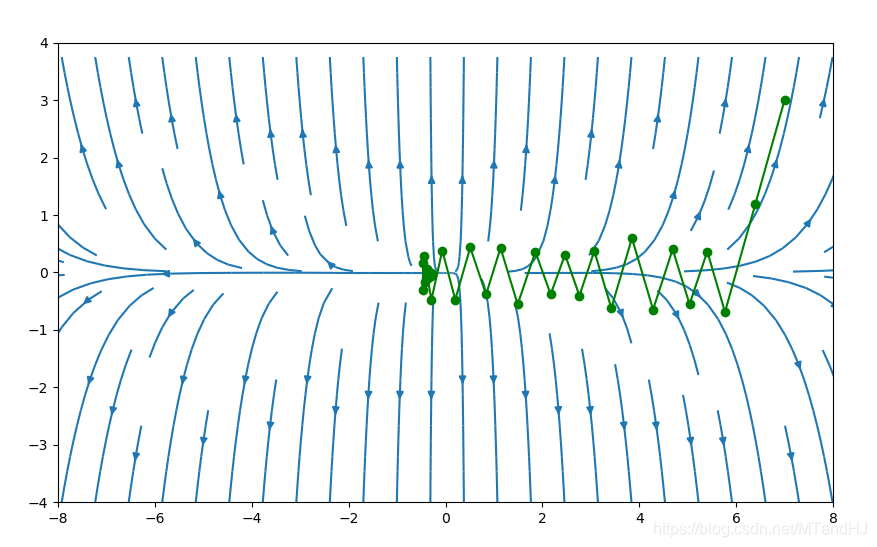
import numpy as np
class GradDescent:
"""
梯度下降方法
"""
def __init__(self, f, x):
assert hasattr(f, "__call__"), "Invalid function {0}".format(f)
self.__f = f
self.x = x
self.y = self.__f(x)
self.__process = [(self.x, self.y)]
@property
def process(self):
"""获得梯度下降过程"""
return self.__process
def grad1(self, update_x, error=1e-5):
"""精确收缩算法
update_x: 用来更新x的函数,这个我们没办法在这里给出
error: 梯度的误差限,默认为1e-5
"""
assert hasattr(update_x, "__call__"), "Invalid function {0}".format(update_x)
error = error if error > 0 else 1e-5
while True:
x = update_x(self.x)
if (x - self.x) @ (x - self.x) < error:
break
else:
self.x = x
self.y = self.__f(self.x)
self.__process.append((self.x, self.y))
def grad2(self, gradient, alpha, beta, error=1e-5):
"""回溯直线收缩算法
gradient: 梯度需要给出
alpha: 下降的期望值 (0, 0.5)
beta:每次更新的倍率 (0, 1)
error: 梯度的误差限,默认为1e-5
"""
assert hasattr(gradient, "__call__"), "Invalid gradient"
assert 0 < alpha < 0.5, "alpha should between (0, 0.5), but receive {0}".format(alpha)
assert 0 < beta < 1, "beta should between (0, 1), but receive {0}".format(beta)
error = error if error > 0 else 1e-5
def search_t(alpha, beta):
t = 1
t_old = 1
grad = -gradient(self.x)
grad_module = grad @ grad
while True:
newx = self.x + t * grad
newy = self.__f(newx)
if newy < self.y - alpha * t * grad_module:
return t_old
else:
t_old = t
t = t_old * beta
while True:
t = search_t(alpha, beta)
x = self.x - t * gradient(self.x)
if (t * gradient(self.x)) @ (t * gradient(self.x)) < error:
break
else:
self.x = x
self.y = self.__f(self.x)
self.__process.append((self.x, self.y))
r = 10.
def f(x):
vec = np.array([1., r], dtype=float)
return 0.5 * (x ** 2) @ vec
def f2(x):
x0 = x[0]
x1 = x[1]
return np.exp(x0+3*x1-0.1) + np.exp(x0-3*x1-0.3) + np.exp(-x0-0.1)
def gradient2(x):
x0 = x[0]
x1 = x[1]
grad1 = np.exp(x0+3*x1-0.1) + np.exp(x0-3*x1-0.3) - np.exp(-x0-0.1)
grad2 = 3 * np.exp(x0+3*x1-0.1) -3 * np.exp(x0-3*x1-0.3)
return np.array([grad1, grad2])
def update(x):
t = -(x[0] ** 2 + r ** 2 * x[1] ** 2) / (x[0] ** 2 + r ** 3 * x[1] ** 2)
x0 = x[0] + t * x[0]
x1 = x[1] + t * x[1] * r
return np.array([x0, x1])
def gradient(x):
diag_martix = np.diag([1., r])
return x @ diag_martix
x_prime = np.array([7, 3.], dtype=float)
ggg = GradDescent(f2, x_prime)
#ggg.grad1(update)
ggg.grad2(gradient2, alpha=0.2, beta=0.7)
process = ggg.process
import matplotlib.pyplot as plt
import matplotlib.path as mpath
fig, ax = plt.subplots(figsize=(10, 6))
w1 = 4
w2 = 10
Y, X = np.mgrid[-w1:w1:300j, -w2:w2:300j]
U = X
V = r * Y
ax.streamplot(X, Y, U, V)
process_x = list(zip(*process))[0]
print(process_x)
path = mpath.Path(process_x)
x0, x1 = zip(*process_x)
ax.set_xlim(-8, 8)
ax.set_ylim(-4, 4)
ax.plot(x0, x1, "go-")
plt.show()标签:RoCE 接受 最优 函数 int assert array png arch
原文地址:https://www.cnblogs.com/MTandHJ/p/10541663.html