标签：获取   思路   alpha   更新   相互   状态   评价   .com   alt   

这篇博客只是为了自己记录，思路比较跳跃。

Policy Gradients

不估计局面的价值，转而预测选取每个动作的概率。因为某些游戏中我们可能会需要在相同的状态下做出随机行为，比如说某些资源有限的游戏，我们不可能一直在某一个地方一直获取资源。

更新函数是\(\theta_{t+1}=\theta_t + \alpha \cfrac{\partial J}{\partial \theta}\)，其中\(J(\theta)\)是对当前参数产生的策略的评价，越高越好。

\(J(\theta)\)中，\(\theta\)的影响来自于两方面，一是在特定状态下的行为选择，二是这个策略到每个状态的概率。行为选择的偏导比较好考虑，然而行为造成的“某些高价值的状态没有到达”这件事情的偏导就没有那么形象了。

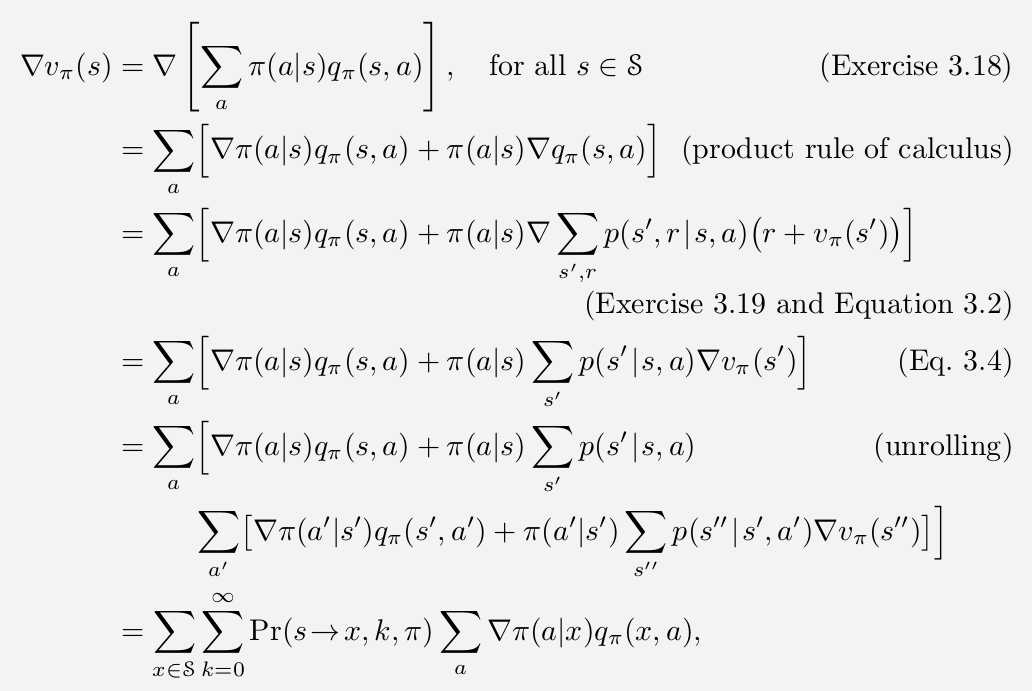
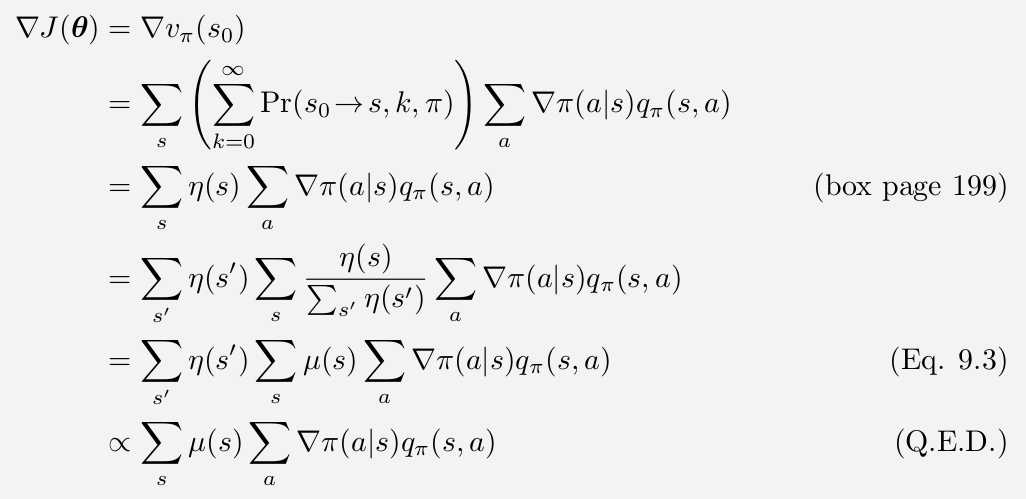
我们把策略对可能到达状态的影响浓缩在了一个\(\mu (x)\)里，表示在该策略下到达\(x\)的概率。

最后关于这个梯度的计算，我自己有一些想法：

• 一是通过蒙特卡洛估计，即使状态量巨大或者无限，状态的密度分布依然会把我们带到密度大的状态，我们的\(q\)值也是策略下的\(q\)值，没有统计到的密度小的状态价值再高也会被密度冲淡，影响不大。
• 二是通过Q-learning or DQN来估计\(q\)值，两个算法相互迭代。

Policy Gradients

标签：获取   思路   alpha   更新   相互   状态   评价   .com   alt   

原文地址：https://www.cnblogs.com/LincHpins/p/10545122.html