标签:而且 迭代 线性回归 方法 data 要求 移动 需要 回归
一般线性回归函数的假设函数为:
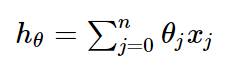
对应的损失函数为:
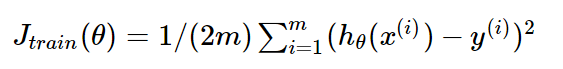
(这里的1/2是为了后面求导计算方便)
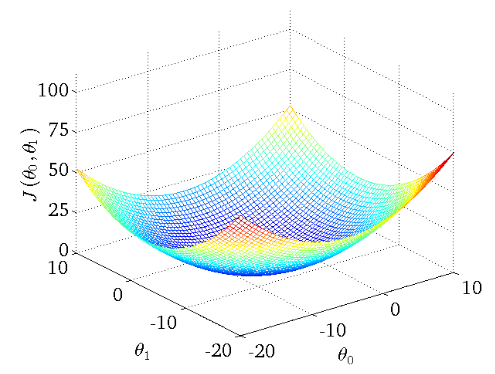
下图作为一个二维参数(,
)组对应能量函数的可视化图:
下面我们来比较三种梯度下降法
我们的目的是要误差函数尽可能的小,即求解weights使误差函数尽可能小。首先,我们随机初始化weigths,然后不断反复的更新weights使得误差函数减小,直到满足要求时停止。这里更新算法我们选择梯度下降算法,利用初始化的weights并且反复更新weights:
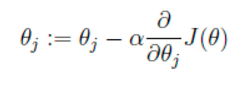
这里代表学习率,表示每次向着J最陡峭的方向迈步的大小。为了更新weights,我们需要求出函数J的偏导数。首先当我们只有一个数据点(x,y)的时候,J的偏导数是:
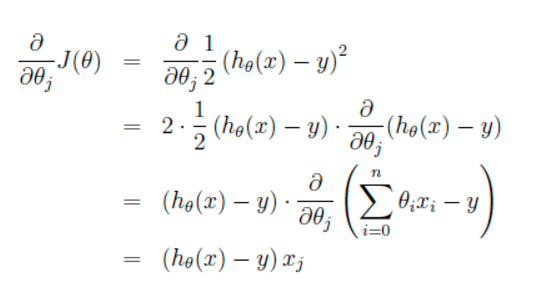
则对所有数据点,上述损失函数的偏导(累和)为:
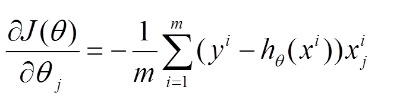
再最小化损失函数的过程中,需要不断反复的更新weights使得误差函数减小,更新过程如下:
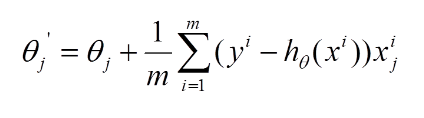 那么好了,每次参数更新的伪代码如下:
那么好了,每次参数更新的伪代码如下:
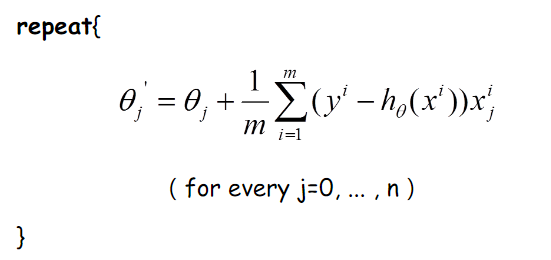
由上图更新公式我们就可以看到,我们每一次的参数更新都用到了所有的训练数据(比如有m个,就用到了m个),如果训练数据非常多的话,是非常耗时的。
下面给出批梯度下降的收敛图:
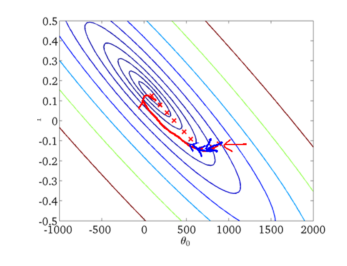
从图中,我们可以得到BGD迭代的次数相对较少。
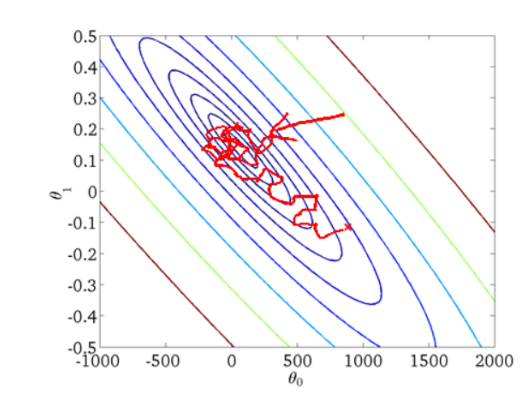
由于批梯度下降每跟新一个参数的时候,要用到所有的样本数,所以训练速度会随着样本数量的增加而变得非常缓慢。随机梯度下降正是为了解决这个办法而提出的。它是利用每个样本的损失函数对θ求偏导得到对应的梯度,来更新θ:
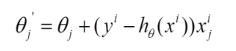
更新过程如下:

随机梯度下降是通过每个样本来迭代更新一次,对比上面的批量梯度下降,迭代一次需要用到所有训练样本(往往如今真实问题训练数据都是非常巨大),一次迭代不可能最优,如果迭代10次的话就需要遍历训练样本10次。但是,SGD伴随的一个问题是噪音较BGD要多,使得SGD并不是每次迭代都向着整体最优化方向。
解释一下为什么SGD收敛速度比BGD要快:
这里我们假设有30万个样本,对于BGD而言,每次迭代需要计算30万个样本才能对参数进行一次更新,需要求得最小值可能需要多次迭代(假设这里是10);而对于SGD,每次更新参数只需要一个样本,因此若使用这30万个样本进行参数更新,则参数会被迭代30万次,而这期间,SGD就能保证能够收敛到一个合适的最小值上了,也就是说,在收敛时,BGD计算了10*30万次,而SGD只计算了1*30万次。
随机梯度下降收敛图如下:
我们可以从图中看出SGD迭代的次数较多,在解空间的搜索过程看起来很盲目。但是大体上是往着最优值方向移动。
所以SGD迭代次数比BGD要多,但是其收敛速度要快于BGD。
我们从上面两种梯度下降法可以看出,其各自均有优缺点,那么能不能在两种方法的性能之间取得一个折衷呢?即,算法的训练过程比较快,而且也要保证最终参数训练的准确率,而这正是小批量梯度下降法的初衷。
MBGD的思想是:每次迭代使用batch_size个样本来对参数进行更新。
这里我们假设batch_size=10,样本数m=1000
更新伪代码如下:
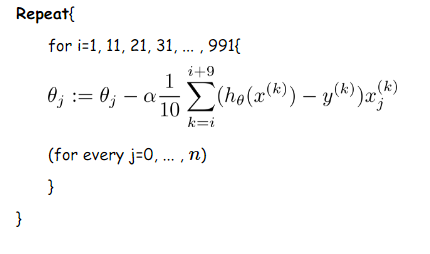
优点:每次使用一个batch可以大大减小收敛所需要的迭代次数,同时可以使收敛到的结果更加接近梯度下降的效果。
缺点:batch_size的不当选择可能会带来一些问题。
批量梯度下降BGD、随机梯度下降SGD和小批量梯度下降MBGD对比
标签:而且 迭代 线性回归 方法 data 要求 移动 需要 回归
原文地址:https://www.cnblogs.com/CuteyThyme/p/10546498.html