标签:else 模型 隐藏 com 背景 总数 递增 估算 nump
基本介绍:
http://www.51testing.com/html/36/489136-831363.html
https://testerhome.com/topics/10381
http://www.doc88.com/p-2445313427576.html
我们在日常的软件测试过程中会发现,在测试的初始阶段,测试人员对测试环境不很熟悉,因此日均发现的软件缺陷数比较少,发现软件缺陷数的增长较为缓慢;随着测试人员逐渐进入状态并熟练掌握测试环境后,日均发现软件缺陷数增多,发现软件缺陷数的增长速度迅速加快;但随着测试的进行,软件缺陷的隐藏加深,测试难度加大,需要执行较多的测试用例才能发现一个缺陷,尽管缺陷数还在增加,但增长速度会减缓,同时软件中隐藏的缺陷是有限的,因而限制了发现缺陷数的无限增长。这种发现软件缺陷的变化趋势及增长速度是一种典型的‘S’曲线,满足Gompertz增长模型的应用条件。模型表达式为:
Y=a*b^(c^T)
其中Y表示随时间T发现的软件缺陷总数,a是当T→∞时的可能发现的软件缺陷总数,即软件中所含的缺陷总数。a*b是当T→0时发现的软件缺陷数,c表示发现缺陷的增长速度。我们需要依据现有测试过程中发现的软件缺陷数量来估算出三个参数a,b,c的值,从而得到拟合曲线函数.
原型代码如下(python)
# coding: UTF-8
import math
import numpy as np
from scipy.optimize import leastsq
###采样点
#project 1
yi=np.array([2,4,4,6,12,15,21,27,39,45,50,54])
#project 2
yi=np.array([6,11,15,20,25,31,33,41,42,44,49,52,53])
ti=np.array(xrange(1,yi.size+1))
total=yi[-1]
def func(p,t):
a,b,c=p
return a*b**(c**t)
def error(p,t,y,s):
print s
return func(p,t)-y
def extra(thread,a,b,c,total,day):
expect=a*thread/100
T=(math.log(math.log(expect/a)/math.log(b)))/math.log(c)
if T>day:
return T-day
else:
return 0
#初始值
p0=[1500,0.078,0.874]
s="Test the number of iteration"
para=leastsq(error,p0,args=(ti,yi,s))
a,b,c=para[0]
print 'a=',a,'b=',b,'c=',c
print '预期bug总数:',a
print '已发现bug总数:' ,total
print '已发现bug占比:',total/a
day=yi.size
print '已花费天数:' ,day
T=extra(95,a,b,c,total,day)
print '为达到发现95的bug还需要%d天'%T
T=extra(90,a,b,c,total,day)
print '为达到发现90的bug还需要%d天'%T
import matplotlib.pyplot as plt
plt.figure(figsize=(8,6))
plt.scatter(ti,yi,color='red',label='Sample Point',linewidth=3)
t=np.linspace(0,yi.size*2,1000)
y=a*b**(c**t)
plt.plot(t,y,color='orange',label='fitting Point',linewidth=2)
plt.legend()
plt.show()
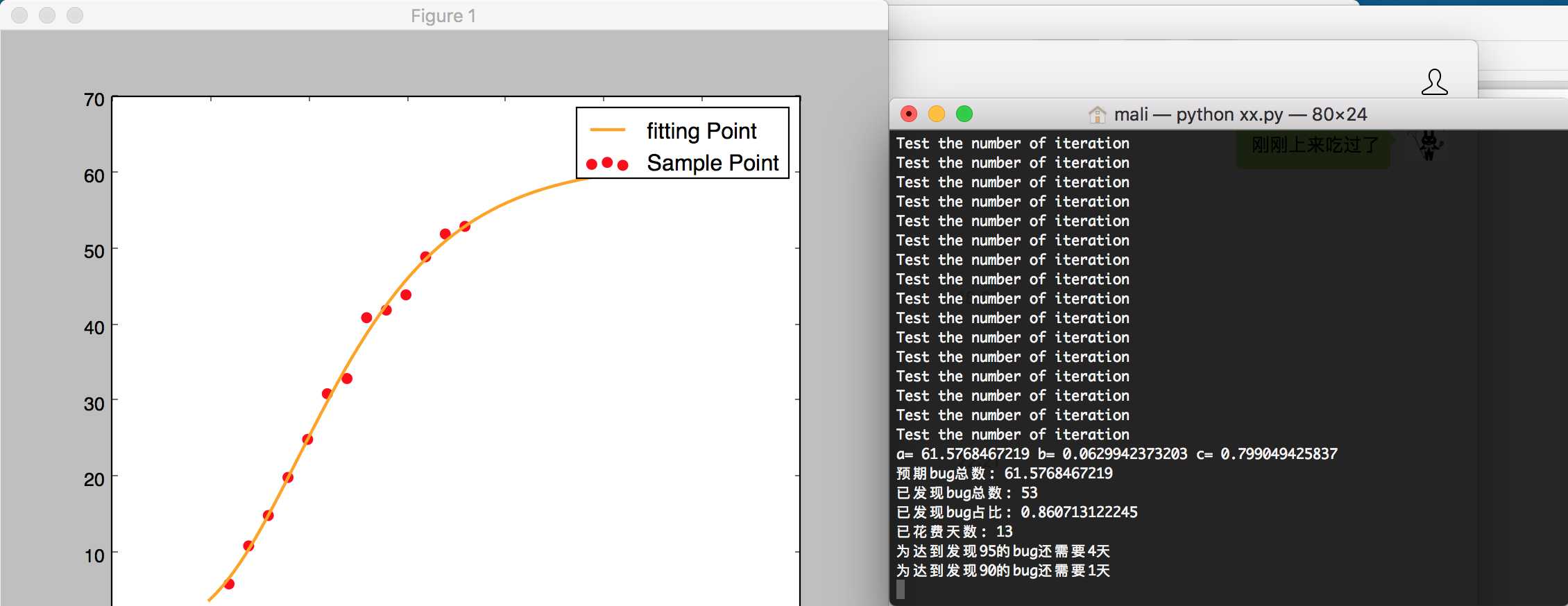
未来可以考虑优化这个预测模型或者采用更好的模型去判断测试退出时间点以及预测漏侧数量
标签:else 模型 隐藏 com 背景 总数 递增 估算 nump
原文地址:https://www.cnblogs.com/opama/p/10549796.html