变形的指派问题

标签：col   最小   整数   方法   承担   复制   矩阵   das   bsp   

工作多于人数的指派问题　　

　　设人数m，工作数n，且n-m>0。

　　1. n/m=k为整数时，需要每人完成k项工作任务。

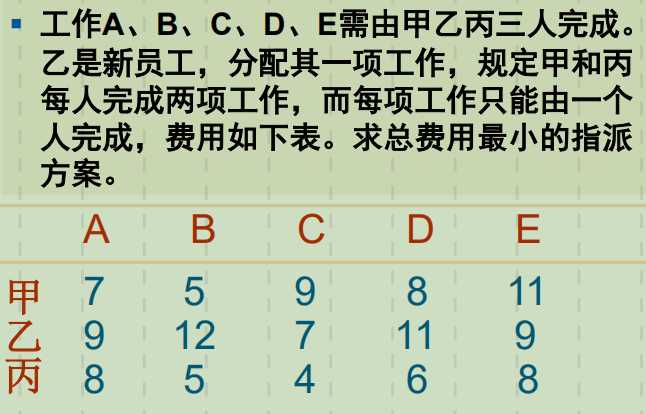
　　解：甲和乙每人分配2项工作，故一个人要当两个人用。在分配矩阵中可以把这两个人每行数据复制成两行，再利用经典指派问题算法进行计算。

　　为什么要利用经典算法？——理由是经典算法已经有成熟高效的计算方法和数学软件。

　　过程如下：

　　1. 每行减去该行最小数。

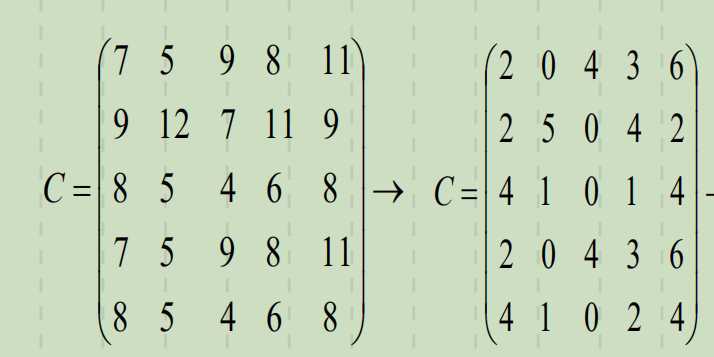
　　2. 每列减去该列最小数。

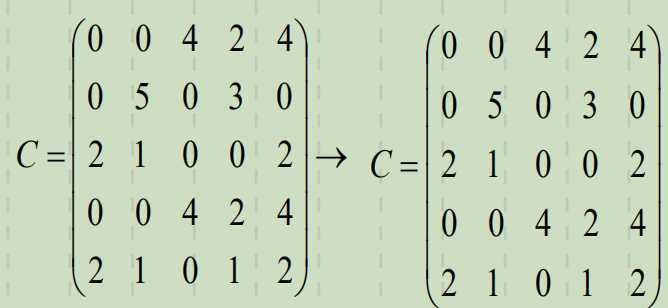
　　3. 试分配。

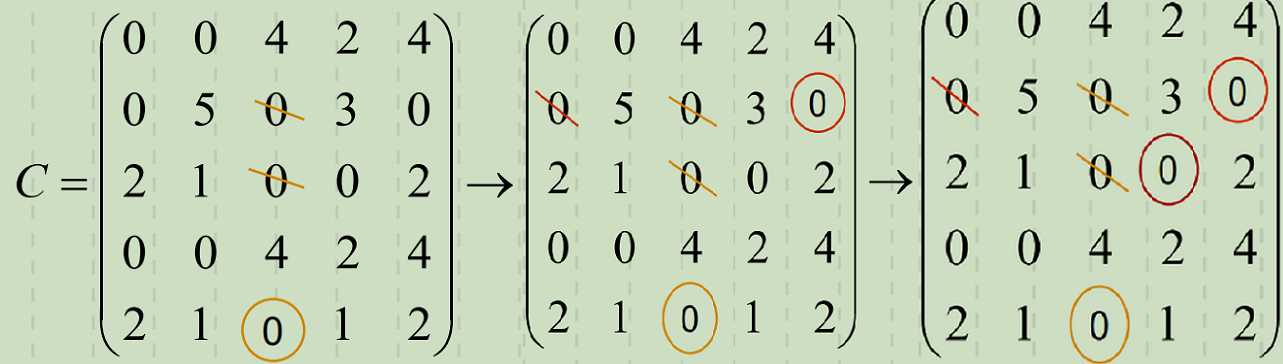
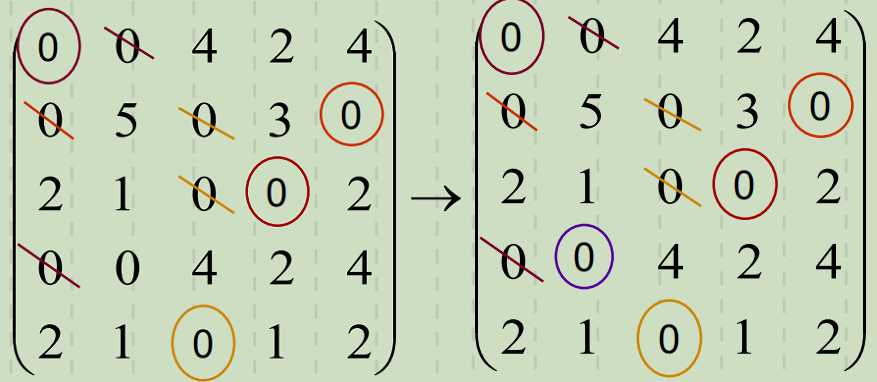
　　计算的最终结果即：

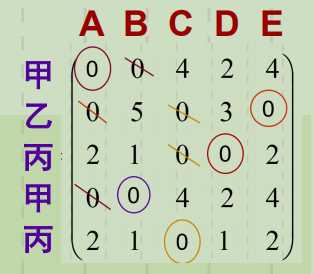
　　甲分配到工作A和B

　　乙分配到工作E

　　丙分配到工作D和C。

　　故最小成本（目标）为：Z=7+5+9+4+6=31

　　2. n/m=k不为整数时，需要每人完成[k]项或[k]+1工作任务。

　　由于每个人最多可能承担[k]+1项工作任务，分配矩阵每行复制成[k+1]行。

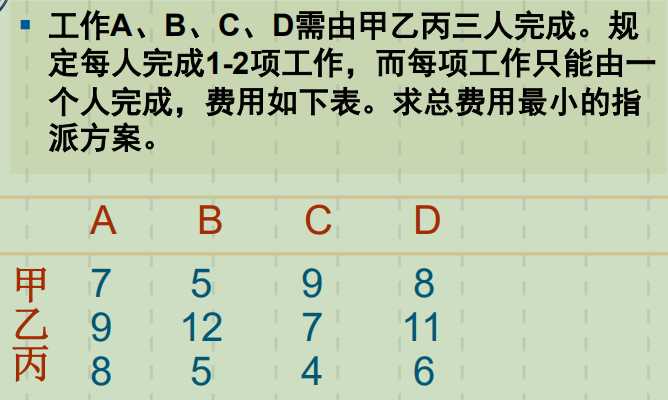
　　1. 构造初始矩阵。

　　2. 每个人限制最多做一项虚拟工作。

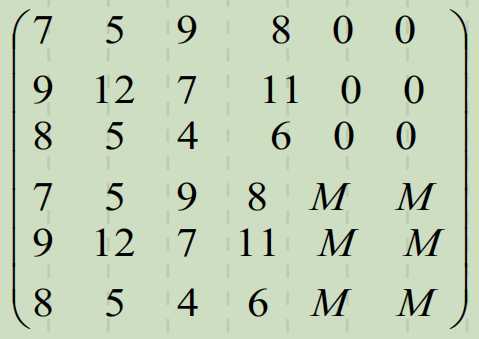
　　3. 每行减去最小数。

　　4. 每列减去最小数。

　　5. 试分配。

　　6. 匈牙利法。

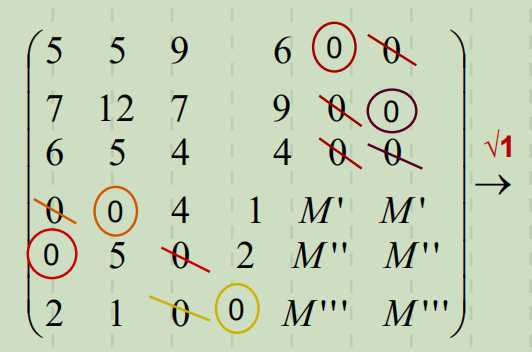
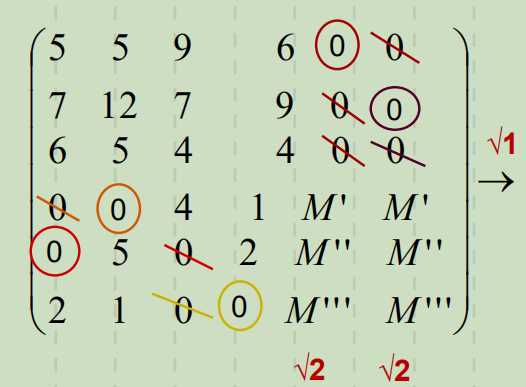
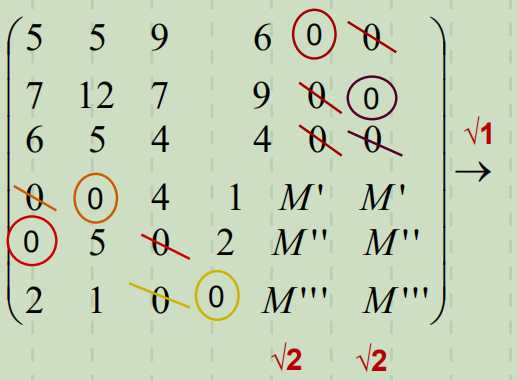
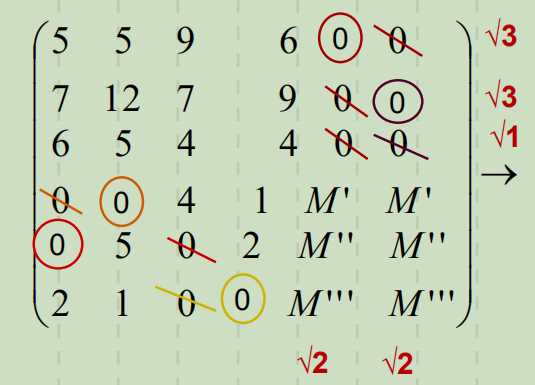
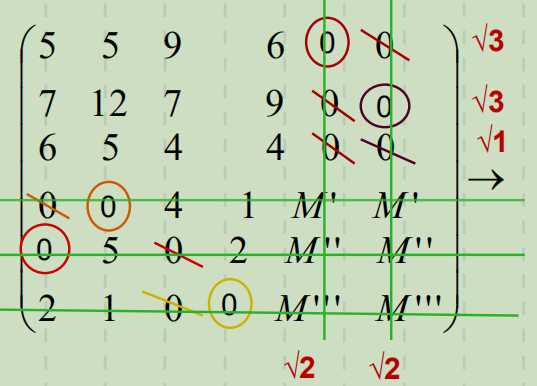
　　最小未覆盖数为4

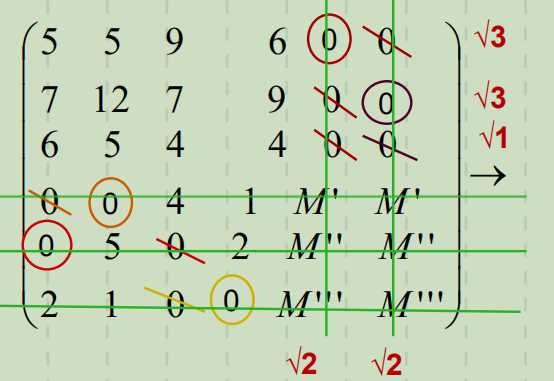
　　7. 调整费用矩阵，再次试分配。

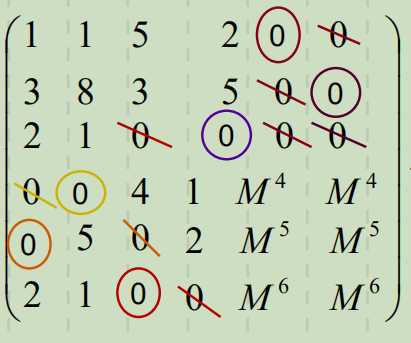
　　最后，

　　甲分配到工作B

　　乙分配到工作A

　　丙分配到工作C和D

　　最小总费用为：Z=5+9+（4+6）=24

变形的指派问题

标签：col   最小   整数   方法   承担   复制   矩阵   das   bsp   

原文地址：https://www.cnblogs.com/fangxiaoqi/p/10545233.html