标签:标准 分布 proc 取值 sim 下一步 process amp 定位
上节介绍过acquistion function(AC函数)是用来利用之前的信息寻找下一个$x_{t+1}$。下面介绍AC函数的具体形式:
目前主流的AC函数主要有三种Probability of Improvement(PI),Excepted Improvement(EI),GP Upper Confidence Bound(GP-UCB)三种。
首先介绍下最基本的数学背景。
记$\mathcal { D } _ { 1 : t } = \left\{ \mathbf { x } _ { 1 : t } , f _ { 1 : t } \right\}$为已经探索过得到的历史信息,其中$f_{t+1}=f(x_{t+1})$,假定我们所需搜寻的下一个值维$x_{t+1}$,且有$f_{t+1}=f(x_{t+1})$。记协方差矩阵K为:
\[\mathbf { K } = \left[ \begin{array} { c c c } { k \left( \mathbf { x } _ { 1 } , \mathbf { x } _ { 1 } \right) } & { \dots } & { k \left( \mathbf { x } _ { 1 } , \mathbf { x } _ { t } \right) } \\ { \vdots } & { \ddots } & { \vdots } \\ { k \left( \mathbf { x } _ { t } , \mathbf { x } _ { 1 } \right) } & { \dots } & { k \left( \mathbf { x } _ { t } , \mathbf { x } _ { t } \right) } \end{array} \right]\]
根据高斯过程的性质,$f_{1:t}$与$f_{t+1}$服从联合高斯分布:
\[\left[ \begin{array} { c } { \mathbf { f } _ { 1 : t } } \\ { f _ { t + 1 } } \end{array} \right] \sim \mathcal { N } \left( \begin{array} { c c } { \mathbf { K } } & { \mathbf { k } } \\ { \mathbf { k } ^ { T } } & { k \left( \mathbf { x } _ { t + 1 } , \mathbf { x } _ { t + 1 } \right) } \end{array} \right) \]
这里有:
\[\mathbf { k } = \left[ k \left( \mathbf { x } _ { t + 1 } , \mathbf { x } _ { 1 } \right) \quad k \left( \mathbf { x } _ { t + 1 } , \mathbf { x } _ { 2 } \right) \quad \cdots \quad k \left( \mathbf { x } _ { t + 1 } , \mathbf { x } _ { t } \right) \right]\]
通过求其边缘密度函数,可以得到:
\[ f _ { t + 1 } | \mathcal { D } _ { 1 : t } , \mathbf { x } _ { t + 1 } = \mathcal { N } \left( \mu _ { t } \left( \mathbf { x } _ { t + 1 } \right) , \sigma _ { t } ^ { 2 } \left( \mathbf { x } _ { t + 1 } \right) \right)\]
其中:
\[\mu _ { t } \left( \mathbf { x } _ { t + 1 } \right) = \mathbf { k } ^ { T } \mathbf { K } ^ { - 1 } \mathbf { f } _ { 1 : t }\]
\[\sigma _ { t } ^ { 2 } \left( \mathbf { x } _ { t + 1 } \right) = k \left( \mathbf { x } _ { t + 1 } , \mathbf { x } _ { t + 1 } \right) - \mathbf { k } ^ { T } \mathbf { K } ^ { - 1 } \mathbf { k }\]
(该推导可以参见Gaussian Processes for machine learning,Williams,2006 附录A2)
有了上面的准备,就可以估计出$x_{t+1}$在任意取值处所服从的正态分布,从而可以设定特定的目标函数去定位下一步最优的$x_{t+1}$
Probability of Improvement(PI)
PI的思想在于基于最大可能概率改进,即假设当前已有的最优采样为$x_+$,满足$\mathbf { x } ^ { + } = \operatorname { argmax } _ { \mathbf { x } _ { i } \in \mathbf { x } _ { 1 : t } } f \left( \mathbf { x } _ { i } \right)$,则
\[\begin{aligned} \mathrm { PI } ( \mathbf { x } ) & = P \left( f ( \mathbf { x } ) \geq f \left( \mathbf { x } ^ { + } \right) \right) \\ & = \Phi \left( \frac { \mu ( \mathbf { x } ) - f \left( \mathbf { x } ^ { + } \right) } { \sigma ( \mathbf { x } ) } \right) \end{aligned}\]
其中$\Phi ( \cdot )$表示标准正态分布的分布函数。
需要注意的是以上对于$x_{t+1}$的求解仅利用了已有信息,并没有很好权衡探索-利用之间的矛盾(对于探索-利用矛盾如果不了解可以阅读强化学习的一些基础内容),因此PI函数还具有以下变形:
\[\begin{aligned} \mathrm { PI } ( \mathbf { x } ) & = P \left( f ( \mathbf { x } ) \geq f \left( \mathbf { x } ^ { + } \right) + \xi \right) \\ & = \Phi \left( \frac { \mu ( \mathbf { x } ) - f \left( \mathbf { x } ^ { + } \right) - \xi } { \sigma ( \mathbf { x } ) } \right) \end{aligned}\]
其中$\xi \geq 0$,一种建议的做法是刚开始训练时$\xi$可以较大,加强探索,随算法迭代,$\xi$应该逐渐减少,加强利用。
Excepted Improvement(EI)
EI的思想在于寻找具有最大改善期望的$x_{t+1}$,记选取$x_{t+1}$后,被改进的函数为$I(x)$,
\[\mathrm { I } ( \mathrm { x } ) = \max \left\{ 0 , f _ { t + 1 } ( \mathrm { x } ) - f \left( \mathrm { x } ^ { + } \right) \right\}\]
我们做需寻找的$x_{t+1}$应满足
\[\mathbf { x } = \underset { \mathbf { x } } { \operatorname { argmax } } \mathbb { E } \left( \max \left\{ 0 , f _ { t + 1 } ( \mathbf { x } ) - f \left( \mathbf { x } ^ { + } \right) \right\} | \mathcal { D } _ { t } \right)\]
期望改进的计算公式还可以进行如下变形:
\[\begin{aligned} \mathbb { E } ( \mathrm { I } ) & = \int _ { \mathrm { I } = 0 } ^ { \mathrm { I } = \infty } \mathrm { I } \frac { 1 } { \sqrt { 2 \pi } \sigma ( \mathbf { x } ) } \exp \left( - \frac { \left( \mu ( \mathbf { x } ) - f \left( \mathbf { x } ^ { + } \right) - \mathrm { I } \right) ^ { 2 } } { 2 \sigma ^ { 2 } ( \mathbf { x } ) } \right) d \mathrm { I } \\ & = \sigma ( \mathbf { x } ) \left[ \frac { \mu ( \mathbf { x } ) - f \left( \mathbf { x } ^ { + } \right) } { \sigma ( \mathbf { x } ) } \Phi \left( \frac { \mu ( \mathbf { x } ) - f \left( \mathbf { x } ^ { + } \right) } { \sigma ( \mathbf { x } ) } \right) + \phi \left( \frac { \mu ( \mathbf { x } ) - f \left( \mathbf { x } ^ { + } \right) } { \sigma ( \mathbf { x } ) } \right) \right] \end{aligned}\]
最终化简结果为:
\[\operatorname { EI } ( \mathbf { x } ) = \left\{ \begin{array} { l l } { \left( \mu ( \mathbf { x } ) - f \left( \mathbf { x } ^ { + } \right) \right) \Phi ( Z ) + \sigma ( \mathbf { x } ) \phi ( Z ) } & { \text { if } \sigma ( \mathbf { x } ) > 0 } \\ { 0 } & { \text { if } \sigma ( \mathbf { x } ) = 0 } \end{array} \right.\]
其中$Z = \frac { \mu ( \mathbf { x } ) - f \left( \mathbf { x } ^ { + } \right) } { \sigma ( \mathbf { x } ) }$,并且$\phi ( \cdot )$为标准正态分布的概率分布函数(pdf),$\Phi ( \cdot )$为标准正态分布的分布函数(cdf)。
EI算法同样可以加入探索-利用的权衡标量$\xi$,满足$\xi \geq 0$,此时有
\[\operatorname { EI } ( \mathbf { x } ) = \left\{ \begin{array} { l l } { \left( \mu ( \mathbf { x } ) - f \left( \mathbf { x } ^ { + } \right) - \xi \right) \Phi ( Z ) + \sigma ( \mathbf { x } ) \phi ( Z ) } & { \text { if } \sigma ( \mathbf { x } ) > 0 } \\ { 0 } & { \text { if } \sigma ( \mathbf { x } ) = 0 } \end{array} \right.\]
GP Upper Confidence Bound(GP-UCB)
Upper Confidence Bound是Condidence bound criteria的一种,同样的还可以将准则设置为Lower Confidence Bound,这两个准则的效果是一样的,形式分别为:
Lower Confidence Bound:\[\mathrm { LCB } ( \mathbf { x } ) = \mu ( \mathbf { x } ) - \kappa \sigma ( x )\]
Upper Confidence Bound:\[\mathrm { UCB } ( \mathbf { x } ) = \mu ( \mathbf { x } ) + \kappa \sigma ( x )\]
其中$\kappa \geq 0$一种选取$\kappa$的方法来自于Srinivas(2010),采用后悔值进行计算,建议采用$\kappa _ { t } = \sqrt { \nu \tau _ { t } }$,
其中超参数$\nu > 0$,这样则有$\mathrm { GP } - \mathrm { UCB } ( \mathrm { x } ) = \mu ( \mathrm { x } ) + \sqrt { \nu \tau _ { t } } \sigma ( \mathrm { x } )$
记$x_*$为全局最优解,在$\nu = 1,\tau _ { t } = 2 \log \left( t ^ { d / 2 + 2 } \pi ^ { 2 } / 3 \delta \right)$时,可以证明当协方差函数(核函数)相当平滑时有
\[\lim _ { T \rightarrow \infty } R _ { T } / T = 0\]
其中,$R _ { T } = \sum _ { t = 1 } ^ { T } f \left( \mathbf { x } ^ { \star } \right) - f \left( \mathbf { x } _ { t } \right)$为后悔值的累计值。
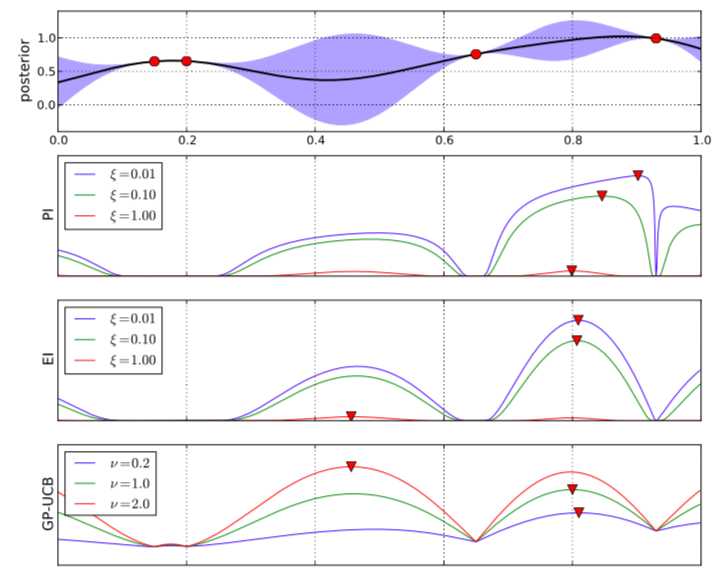
上图给出了上述三种方法的求解示例,不同颜色的线代表不同超参数下贝叶斯框架估计出的AC函数值,阴影部分则表示估计出的方差大小,PI方法趋向于选择概率上最大可能改进现有最好情况的点,EI方法则寻找的是带来改善效果期望值最大的点,GP-UCB则是将均值加方差作为目标函数。
标签:标准 分布 proc 取值 sim 下一步 process amp 定位
原文地址:https://www.cnblogs.com/statruidong/p/10558089.html