标签：das scan each input eth copy ORC 等于 blog
A plane is flying at a constant height of hh meters above the ground surface. Let‘s consider that it is flying from the point (−109,h)(−109,h) to the point (109,h)(109,h) parallel with OxOx axis.
A glider is inside the plane, ready to start his flight at any moment (for the sake of simplicity let‘s consider that he may start only when the plane‘s coordinates are integers). After jumping from the plane, he will fly in the same direction as the plane, parallel to OxOx axis, covering a unit of distance every second. Naturally, he will also descend; thus his second coordinate will decrease by one unit every second.
There are ascending air flows on certain segments, each such segment is characterized by two numbers x1x1 and x2x2 (x1<x2x1<x2 ) representing its endpoints. No two segments share any common points. When the glider is inside one of such segments, he doesn‘t descend, so his second coordinate stays the same each second. The glider still flies along OxOx axis, covering one unit of distance every second.
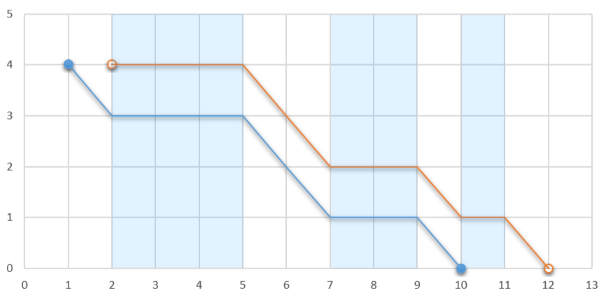
If the glider jumps out at 1 , he will stop at 10 . Otherwise, if he jumps out at 2 , he will stop at 12 . Determine the maximum distance along Ox axis from the point where the glider‘s flight starts to the point where his flight ends if the glider can choose any integer coordinate to jump from the plane and start his flight. After touching the ground the glider stops altogether, so he cannot glide through an ascending airflow segment if his second coordinate is 0 .
The first line contains two integers nn and hh (1≤n≤2⋅105,1≤h≤109)(1≤n≤2⋅105,1≤h≤109) — the number of ascending air flow segments and the altitude at which the plane is flying, respectively.
Each of the next nn lines contains two integers xi1xi1 and xi2xi2 (1≤xi1<xi2≤109)(1≤xi1<xi2≤109) — the endpoints of the ii -th ascending air flow segment. No two segments intersect, and they are given in ascending order.
Print one integer — the maximum distance along OxOx axis that the glider can fly from the point where he jumps off the plane to the point where he lands if he can start his flight at any integer coordinate.
3 4
2 5
7 9
10 11
10
5 10
5 7
11 12
16 20
25 26
30 33
18
1 1000000000
1 1000000000
1999999999
In the first example if the glider can jump out at (2,4)(2,4) , then the landing point is (12,0)(12,0) , so the distance is 12−2=10 12−2=10 .
In the second example the glider can fly from (16,10)(16,10) to (34,0)(34,0) , and the distance is 34−16=18 34−16=18 .
In the third example the glider can fly from (−100,1000000000)(−100,1000000000) to (1999999899,0)(1999999899,0) , so the distance is 1999999899−(−100)=19999999991999999899−(−100)=1999999999 .
题意：给你n个无重力地带，飞机可以从高度h的任意位置开始滑行，问你最远能滑行多远。
思路：（orz做的时候想三分，结果wa了，经过网上题解的调教，原来二分就可以了）首先，我们肯定是从某个无重力地带开始滑行，但是挨个枚举肯定不行，然后就二分Orz
二分注重的就是个单调性，这题比较隐蔽，我们可以发现从左往右，价值越来越大（无重力地带的总长度是越来越长，免费长度，相当于白给），另外花费（两两无重力地带之间的区域，即飞机会下降的区域）也是随着右移越来越大，这样我们可以预处理价值和花费，注意cost【n】 = 2e9+1,因为最后一个无重力地带后面是无限长的。
这样，对于第一个起点，我们拥有高度h可以花费，也就是说找到第一个大于等于高度h的花费，可以用lowerbound；当然，但我们要想后枚举起点的时候h可以加上该起点之前的前缀和（毕竟终点要在起点之后，二分终点的时候加上起点前的值就相当于从该起点后查询）
#include<bits/stdc++.h> using namespace std; int n,h; const int maxn = 2e5+5; int l[maxn]; int r[maxn]; int add[maxn]; int cost[maxn]; int main() { scanf("%d%d",&n,&h); for(int i=1;i<=n;i++) { scanf("%d%d",&l[i],&r[i]); } cost[n] = 2e9+10; for(int i=1;i<n;i++) { cost[i] = cost[i-1] + l[i+1] - r[i]; add[i] = add[i-1] + r[i] - l[i]; } add[n] = add[n-1] + r[n] - l[n]; int ans = 0; for(int i=1;i<=n;i++) { int t = lower_bound(cost+1,cost+1+n,cost[i-1]+h)-cost; ans = max(ans,add[t]-add[i-1]+h); } printf("%d\n",ans); }
标签：das scan each input eth copy ORC 等于 blog
原文地址：https://www.cnblogs.com/iwannabe/p/10560845.html
