标签:ima mat 目标 条件 end log 训练 想法 利用
目录
原问题,带等式约束,也带不等式约束的一般约束问题
\[
\begin{cases} \min_{x}f(x)\s.t \begin{cases} m_i(x)>=0, i=1,..,m\n_j(x)=0,j=1,..,m\\end{cases}
\end{cases}\tag{1}
\]
构造lagrange乘子法
\[
L(x,\lambda_i,\eta_j)= f(x)-\sum_{i=1}^{m}\lambda_im_i(x)-\sum_{j=1}^{n}\eta_j \tag{2}
\]
\[ \begin{cases} \min_{x} max_{\lambda_i,\eta_j} L(R^p)\s.t \lambda_i>=0 \end{cases} \]
上述两个问题的等价性证明
如果x不满足约束\(m_i(x)\),则\(\lambda_i>=0\),同时\(m_i(x)<\),则\(L(R^{p},\lambda,\eta)\)趋近无穷,反之,则存在最大值
\[
min_{x} max_{\lambda,\eta}=min_{x}(max f满足条件,max f不满足约束)\\=min_{x} max_{\lambda,\eta}{f满足条件}
\]
对偶问题: 关于\(\lambda,\eta\)的最大化问题
\[max min L(x,\lambda,\eta)\s.t \lambda_i>=0\]
弱对偶问题:对偶问题<=原问题
证明: \(max_{x} min(\lambda \eta ) L<=min_{\eta,\lambda } max_{x} L\)
\[
\underbrace{\min_{x}L(x,\lambda,\eta)}_{A(\lambda,\eta)}<=L(x,\lambda,\eta)<=\underbrace{\max_{\lambda,\eta} L(x,\lambda,\eta)}_{B(x)}
\]
hard-margin SVM、 soft-margin SVM 、kernel SVM
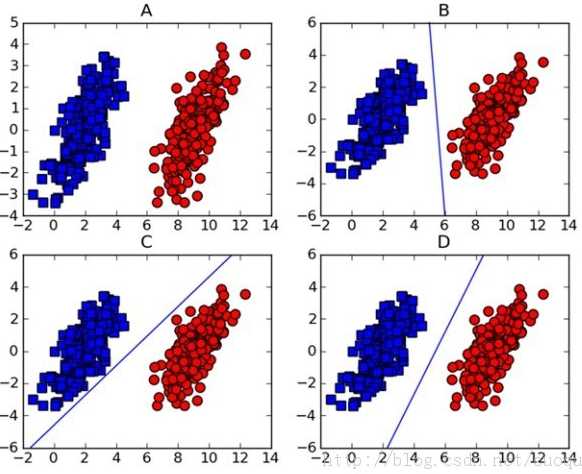
对于A子图,可以用一个超平面(\(w^Tx+b\))去分类两类数据,建立如下的数学模型
\[ f(w,b)=sign(w^Tx+b)\]
B,C,D子图提供了超平面都可以分类,显然B,C图的超平面的鲁棒性不如D图。SVM就是找到最好的一个超平面,怎么衡量好呢?找到平面离样本点的距离最大
首先,看下margin的定义
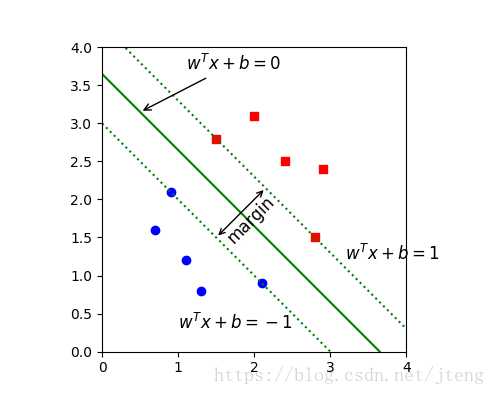
\[ margin(w,b) = min(\frac{|w^Tx_i+b|}{||w||})\]
接下来
数学模型:
\[\begin{cases} \max margin(w,b)\\ st. y_i(w^Tx_i+b)>0\end{cases}\]
\[\Longrightarrow\begin{cases} max \frac{1}{||w||}min(y_i(w^Tx_i+b))\\ st. y_i(w^Tx_i+b)>0\end{cases}\]
注意,\(y_i(w^Tx_i+b)>0\),所以\(\exists r>0, min(y_i(w^Tx_i+b))=r\),可令\(r=1\),这是对超平面范数的固定作用,因为\(y=w^Tx+b\)和\(y=2w^T+2b\)是同一个超平面,总能找到缩放\(w,b\)使得,可以将\(r\)缩放到1
\[\Longrightarrow\begin{cases} max \frac{1}{||w||}\\ st. y_i(w^Tx_i+b)>=1\end{cases}\]
\[\Longrightarrow\begin{cases} \min \frac{1}{2}w^Tw\\ st. y_i(w^Tx_i+b)>=1\end{cases}\]
这是一个土二次规划问题
利用lagrange乘子法得出对偶问题
带约束
\[\begin{cases} \min \frac{1}{2}w^Tw\\ st. y_i(w^Tx_i+b)-1>=0\end{cases}\]
\[ \Longrightarrow L(w,b,\lambda)=\frac{1}{2}w^Tw-\sum_{i=1}^{N}\lambda_i(1-y_i(w^Tx_i+b)\]
无约束
\[ \begin{cases}min_{w,b} max_{\lambda}L(w,b,\lambda) \\ s.t \lambda_i>=0\end{cases}\]
此时关于\(w,b\)无约束的。
对\((L(w,b,\lambda))\) 对\(w\),\(b\)求偏导
\[
\frac{\partial L}{\partial w}=w+\sum_{i=1}^{N}y_ix_i\lambda_i=0 \Longrightarrow w=-\sum_{i=1}^{N}y_ix_i\lambda_i\\frac{\partial L}{\partial b}=-\sum_{i=1}^{N}\lambda_iy_i=0
\]
带回\(L(w,b,\lambda)\),可得对偶问题
\[ \begin{cases} max_{\lambda}L(w,b,\lambda ) =-\frac{1}{2}\sum_i^N\sum_j^N\lambda_i \lambda_jy_iy_jx_i^Tx_j +\sum_i^N\lambda_i \\ s .t. \sum_{i=1}^N\lambda_iy_i,\lambda_i>=0\end{cases} \Longrightarrow\\\begin{cases} min_{\lambda}L(w,b,\lambda ) =\frac{1}{2}\sum_i^N\sum_j^N\lambda_i \lambda_jy_iy_jx_i^Tx_j -\sum_i^N\lambda_i \\ s .t. \sum_{i=1}^N\lambda_iy_i,\lambda_i>=0\end{cases}\]
满足 KKT
\[
\begin{cases}
\frac{\partial L}{\partial w}=0,\frac{\partial L}{\partial b}=0,\frac{\partial L}{\partial \lambda}=0\\lambda_i(y_i(w^Tx_i+b)-1)=0\\lambda_i>=0\y_i(w^Tx_i+b)-1>=0
\end{cases}
\]
如果存在\((x_k,y_k)=+1or -1\)使得?\(y_i(w^Tx_i+b)-1=0\)即可求解\(b=y_k-\sum_{i=0}^{N}\lambda_ix_i^Tx_k\)
代入模型
\[ f(x)=sign(\sum_i^Na_iy_ix_i^Tx+y_k-\sum_{i=0}^{N}\lambda_ix_i^Tx_k)\]
注意,对于任意的训练样本,总有\(\lambda_i=0\)或者\(y_if(x_i)=1\),如果\(\lambda_i>0\),说明样本点落在最大间隔的边界上,这些点就是支持向量,这条边界\(w^Tx+b=1or-1\)
想法:允许一部分样本可以不被正确分类
\[ \min_{w,b} \frac{1}{2}w^Tw+loss \]
0-1损失 个数
\[loss=\sum_{i=1}^NI\{y_i(w^Tx+b)<1\}\]
数学性质不好,不连续
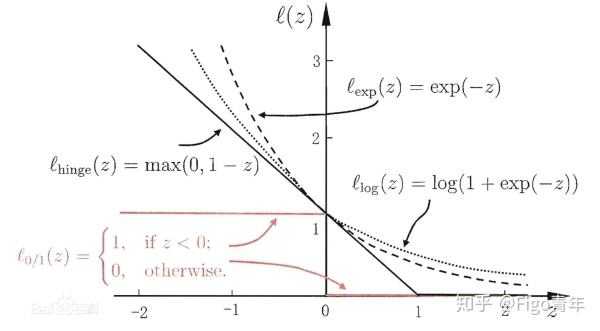
0-1损失 距离 hinge loss
\[
loss = \begin{cases}
0 , y_i(w^Tx_i+b)>=0,\1-y_i(w^tx_i+b), y_i(w^Tx_i+b)<1\\end{cases}
\]
\[ loss_{max} = max(0,1-y_i(w^Tx_i+b)=1-z) \]
此时优化问题,令\(\xi_i=1-y_i(w^Tx_i+b)\)
\[
\min \frac{1}{2}w^Tw+\sum_{i=1}^{N}\xi_i\s.t \begin{cases}
y_i(w^Tx_i+b)>=1-\xi_i\\xi_i>=0
\end{cases}
\]
指数损失(exponential loss )
\[
l_{exp}(z)=exp(-z)
\]
对率损失logistic loss
\[
l_{log}(z)=log(1+exp(-z))
\]
设 \(\chi\)为输入空间(Input Space), \(\mathrm{H}\)为特征空间(Feature Space,一定是希尔伯特空间),存在一个映射
\[
\varphi : \chi \rightarrow \mathrm{H}
\]
对任意的 \(x, y \in \mathrm{X}\),函数 \(K(x, y)\),满足
\[
K(x, y)=<\varphi(x), \varphi(y)>
\]
则称 \(K(x, y)\)为核函数。可以看出,我们并不需要知道输入空间和特征空间满足的映射关系 ,只需要知道核函数就可以算出,输入空间中任意两点映射到特征空间的内积。
标签:ima mat 目标 条件 end log 训练 想法 利用
原文地址:https://www.cnblogs.com/xiemaycherry/p/10560865.html