标签:概率 code 个学生 class 取出 math 反思 图片 lin
一般的,在含有\(M\)件次品的\(N\)件产品中,任取\(n\)件,其中恰有\(X\)件次品,则事件\(\{X=k\}\)发生的概率为\(P(X=k)=\cfrac{C_M^k\cdot C_{N-M}^{n-k}}{C_N^n}\),(\(k=0,1,2,\cdots,m\)),其中\(m=min\{M,n\}\),且\(n\leq N\),\(M\leq N\),\(n\),\(M\),\(N\in N^*\),称这样的分布列为超几何分布列,如果随机变量\(X\)的分布列具有下表的形式,则称随机变量\(X\)服从超几何分布。
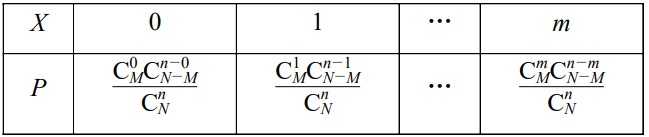
如果\(X\)服从参数为\(n\),\(M\),\(N\)的超几何分布,记作\(X\sim H(n,M,N)\),其数学期望\(E(X)=\cfrac{nM}{N}\)。
①10件产品中含有3件次品,从中任意取4件产品,所取出的次品件数服从超几何分布;
②袋中有8红球4白球,从中任意摸出5个球,摸出红球个数服从超几何分布;
③某班45个学生,女生20人,现从中选7人做代表,代表中所含女生的人数服从超几何分布;
④15张卡片中含有5件写有“奖”字,从中任意取3件产品,所取出的卡片中含有奖字的卡片张数服从超几何分布;
⑤10位代表中有5位支持候选人\(A\),随机采访3人,其中支持候选人\(A\)的人数服从超几何分布;
⑥盘中装有10个粽子,豆沙粽2个,肉粽3个,白粽5个,从中任选3个,取到的豆沙粽的个数服从超几何分布;
注意:在具体题目中,可能需要将上述的三类数据转化为两类数据:豆沙粽子和非豆沙粽子。



解后反思:
①超几何分布的特点是:总体有A,B两类元素(如男女、正品次品等)组成,从总体中不放回的取出一定数目的元素,其中含有一类元素的个数即服从超几何分布;
②在具体题目中给定的数据种类比较多时,可能需要将其转化为需要的两类。比如本题目第(1)问中,为求解选出的4人中有2个种子选手,且种子选手来自同一协会,我们需要将甲乙两个协会的给定人数转化为两类:情形一,一类为甲协会的2个种子选手,另一类为3个非种子选手,此时将乙协会的两个人不予考虑;情形二,一类为乙协会的3个种子选手,另一类为3个非种子选手,此时将甲协会的两个人不予考虑;本题目第(2)问中,需要将8人分为两类:一类是5个种子选手,另一类是3个非种子选手。
③超几何分布中随机变量取各个值的概率是古典概型,使用古典概型的分式进行计算。
标签:概率 code 个学生 class 取出 math 反思 图片 lin
原文地址:https://www.cnblogs.com/wanghai0666/p/10534758.html