标签:序列 image 时间 处理器 初始 str 选项 mamicode 替换
前言:
? 线性探测法是在散列位置的相邻点开始探测,这会引起很多问题,于是各种优化版本例如平方探测、双散列等被提出来改进其中的聚集问题。但是探测相邻位置和第二次散列相比,显然探测相邻位置更有优势,所以线性探测仍然是实用的,甚至是最佳选择。
? 跳房子散列的思路:用事先确定的,对计算机底层体系结构而言最优的一个常数,给探测序列的最大长度加个上界。这样做可以给出常数级的最坏查询时间,并且与布谷鸟散列一样,查询可以并行化,以同时检查可用位置 的有限集。
布谷鸟散列:
? 要点:
? a)依然是线性探测
? b)探测长度\(i\)有个上限
? c)上限是提前定好的,跟计算机底层体系结构有关系
? 跳房子散列规则:
? a)最大探测上界MAX_DIST? = 4
? b)散列位置\(hash(x)\),则探测位置为 \(hash(x)+0\)、\(hash(x)+1\)、\(hash(x)+2\)、\(hash(x)+3\)。
? c)下例:
图解说明:
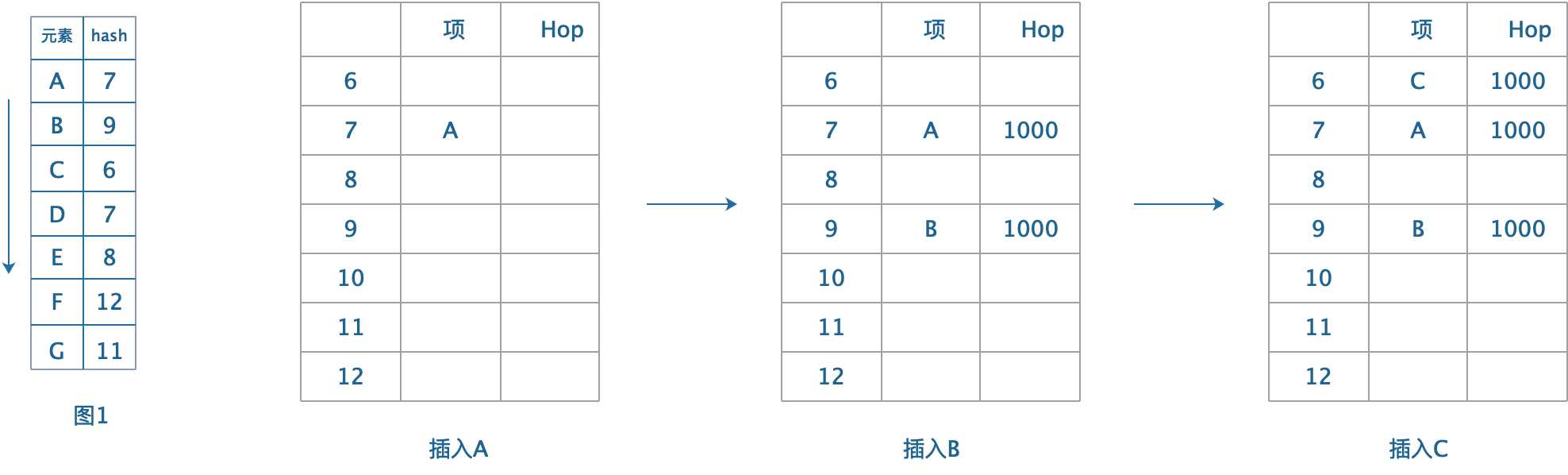
? 图1展示A~G的元素,右侧是他们的散列值。图表中的Hop表示探测位置是否被占用,比如“0010”,说明\(hash(x)+2\)位置被使用。用四位码表示具体位置。
? a)插入A,A的散列位置是7,则Hop[7]的第0个位置被占用,记作“1000”;
? b)插入B,B的散列位置是9,则Hop[9]的第0个位置被占用,记作“1000”;
? c)插入C,C的散列位置是6,则Hop[6]的第0个位置被占用,记作“1000”;以上未发生冲突。
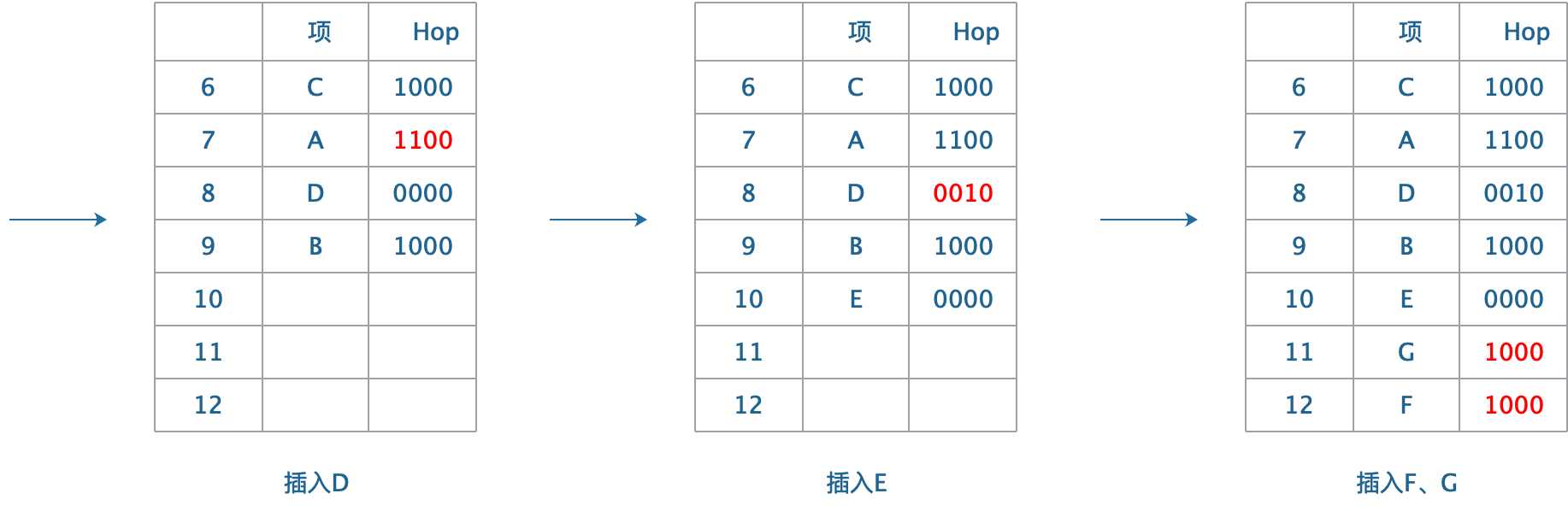
? d)插入D,D的散列位置是7,发生冲突,位置7已经存在值A,开始线性探测,探测下一个位置\(hasx(x)+1 = 8\),位置8未被占用,可插入,则Hop[7]的第1个位置被占用,将Hop[7]记作“1100”;
? e)插入E,E的散列位置是8,发生冲突,位置8已经存在值D,开始线性探测,探测下一个位置$hasx(x)+1 =9 \(,位置9已经存在值B,继续探测下一个位置\)hasx(x)+2 = 10$,位置10未被占用,可插入,测试Hop[8]的第2个位置被占用,将Hop记作“0010”;
? f、g)插入F、G。未发生冲突,同上插入。
? 上述跳房子插入很简单,我们插入一个值,如果在它的hash位置发生冲突,即在上界范围内线性探测下一个位置,知道达到上界,如果有空位置则插入。
问:如果线性探测,直到上界都无法插入呢?
答:当我们上界设置得不够大时,这种情况是必须考虑的。此时的插入流程将会稍微负责。
例如:我们在上述例子中继续插入H,散列值为9。我们探测位置9、10、11、12都被占用,只能到13,但是位置13明显超过上界,即\(hash(x)+3\)都未能找到可插入点。那我们将找一个值y来替换掉。并把它重置到位置13。可以去到位置13的值只有散列值为10、11、12、13的值。如果我们检查Hop[10],它的值为“0000”,没有可以替换的候选项,于是我们检查Hop[11],它的值为“1000”,其值为G,可以被放到位置13。于是我们将元素G放到位置13,将11空出来,插入H。
? 跳房子散列比较简单,是一种比较新的算法,但是初始的实验结果很有前途,特别是对那些使用多处理器并且需要大量并行和并发的应用而言。
? 但是布谷鸟散列和跳房子散列还处于实验室状态,能否在实际中代替线性探测法或者平方探测法,还有待验证。
标签:序列 image 时间 处理器 初始 str 选项 mamicode 替换
原文地址:https://www.cnblogs.com/dhcao/p/10568822.html