标签:int ext details 思路 找规律 efi inf 规律 bit
如图p1.png所示的螺旋折线经过平面上所有整点恰好一次。 对于整点(X, Y),我们定义它到原点的距离dis(X, Y)是从原点到(X, Y)的螺旋折线段的长度。 例如dis(0, 1)=3, dis(-2, -1)=9 给出整点坐标(X, Y),你能计算出dis(X, Y)吗? 【输入格式】 X和Y 对于40%的数据,-1000 <= X, Y <= 1000 对于70%的数据,-100000 <= X, Y <= 100000 对于100%的数据, -1000000000 <= X, Y <= 1000000000 【输出格式】 输出dis(X, Y) 【样例输入】 0 1 【样例输出】 3
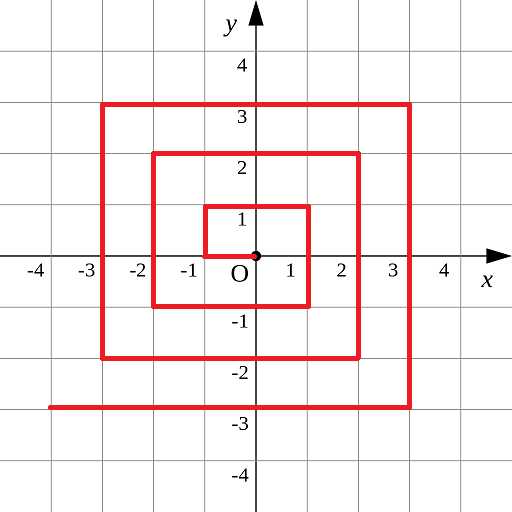
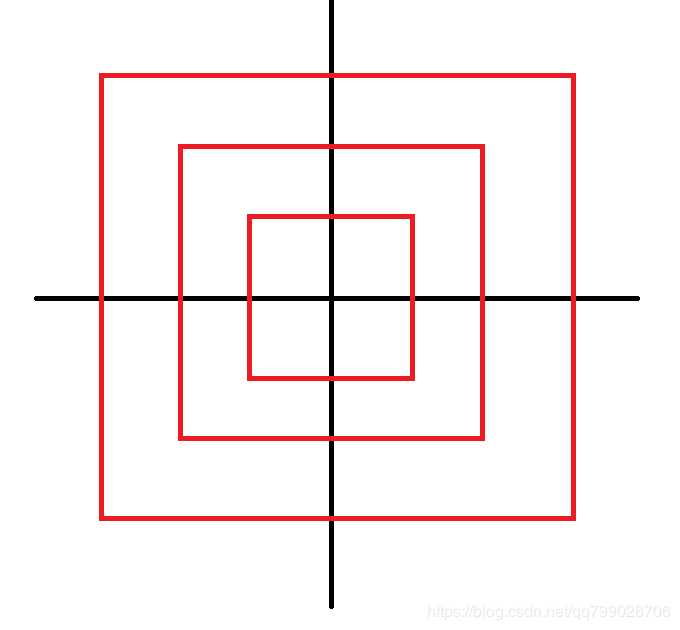
这题大概想了40分钟吧,开始看到别人的思路是把四个象限分一下,然后找规律递推公式,对自己有点启发,于是写出了以下代码:
#include <bits/stdc++.h> #define ll long using namespace std; int main() { ll x, y; scanf("%d%d", &x, &y); ll k = max(abs(x), abs(y)); ll sum1 = 0, sum2 = 0; for (int i = 0; i < k; i++) sum1 += 8*i; if (x==-k&&y!=-k) sum2 += y-x; else if (y==k&&x!=-k) sum2 += y+x+2*k; else if (x==k&&y!=k) sum2 += x-y+4*k; else if (y==-k&&x!=k) sum2 += -(x+y)+6*k; ll ans = sum1 + sum2; printf("%ld", ans); }
但是写完后去搜又发现有个博主思路大致和我差不多,但是后面的处理写的比我好的多,代码如下:
#include <bits/stdc++.h> using namespace std; int main() { long x, y; scanf("%d%d", &x, &y); long n = max(abs(x), abs(y));// 判断所在点所在的正方形 long sum1 = 4*(n-1)*n;//1.计算之前正方形的长度和 //2.计算点(-n, -n) 到点(x, y)的距离, 考虑清楚情况 long sum2 = 0; long d1 = x+n, d2 = y+n; if (y>x) sum2 += d1+d2; else sum2 += 8*n-(d1+d2); printf("%ld", sum1+sum2); return 0; }
感谢大佬:https://blog.csdn.net/qq799028706/article/details/84312062
标签:int ext details 思路 找规律 efi inf 规律 bit
原文地址:https://www.cnblogs.com/wizarderror/p/10581731.html