标签：des   style   blog   http   color   io   os   ar   java   

Delta-wave

A triangle field is numbered with successive integers in the way shown on the picture below. 



The traveller needs to go from the cell with number M to the cell with number N. The traveller is able to enter the cell through cell edges only, he can not travel from cell to cell through vertices. The number of edges the traveller passes makes the length of the traveller‘s route. 

Write the program to determine the length of the shortest route connecting cells with numbers N and M. 

6 12 

3

一条可以利用建立坐标系做的题目。

引用：http://acm.hdu.edu.cn/discuss/problem/post/reply.php?postid=18719&messageid=1&deep=0

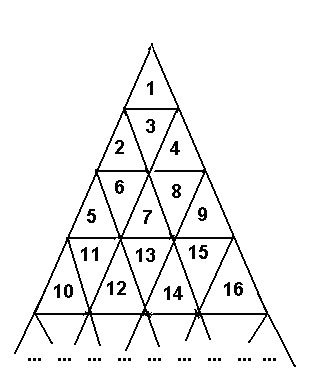
我们把上下两个相连的三角形构成的菱形看做一个格，左斜线看做横坐标，右斜线看做纵坐标，也是四个方向(0,-1),(0,1),(-1,0),(1,0)变化，那么就相当于直角坐标了。

从(x1,y1)到(x2,y2)，这是斜角坐标，距离dis=abs(x1-x2)+abs(y1-y2);我们还需要考虑菱形中的移动，这个都是一层移动一次。

所以答案ans=dis+abs(a-b)=abs(x1-x2)+abs(y1-y2)+abs(a-b)，其中a和b表示各自层数，x1,y1,x2,y2表示两个数所在菱形在斜角坐标系的位置。

不过为什么这样会正确？好像还是很难解析清楚，我理解这是一个规律，跨过了两个不同的斜边，就会得到最短的路径了，因为本题一定要走边，不能走顶点跨到下一个三角形的，故此上下左右的边的最小相隔边数，就是题目要求的最短距离数了。也就可以想象为跨过三角形的三个边，三个方向的边，刚好是上下的h高度边，左斜线的x边，右斜线的y边，（有人也喜欢用x，y，z）那么就肯定是最短路径了。

也可以直接利用数学的方法，然后加点暴力法算出来的，之前做过，不重复了。

#include <stdio.h>
#include <vector>
#include <string.h>
#include <algorithm>
#include <iostream>
#include <string>
#include <limits.h>
#include <stack>
#include <queue>
#include <set>
#include <map>
#include <math.h>
using namespace std;

int main()
{
	int n, m;
	while (scanf("%d %d", &n, &m) != EOF)
	{
		int nh = (int)sqrt(double(n-1));
		int mh = (int)sqrt(double(m-1));

		int nx = (n - nh*nh - 1) >> 1;
		int mx = (m - mh*mh - 1) >> 1;

		int ny = ((nh + 1) * (nh + 1) - n) >> 1;
		int my = ((mh + 1) * (mh + 1) - m) >> 1;

		printf("%d\n", abs(nh-mh) + abs(nx-mx) + abs(ny-my));
	}
	return 0;
}

HDU 1030 Delta-wave 数学题解

标签：des   style   blog   http   color   io   os   ar   java   

原文地址：http://blog.csdn.net/kenden23/article/details/40264043