标签:算法 中心 代码 htm 题目 情况下 经典 gen --
写这篇博客来源于一次面试的经历。不过并不是我被面试,而是我面试别人。如何用两个栈实现一个队列?这算是一个经典的面试题。因为它经常被拿来用。如果对栈和队列比较掌握的人,就可以轻松的答出来。
然而,那天坐在对面的面试者直接抛出:如何用有限个栈模拟常数效率操作的队列呢?作为一个面试官,我佯装镇定,因为这个和用栈实现队列可是一个天上一个地下的区别。听他说完。之后几个小时的面试,我根本无心面试,脑子里一直在想:他刚才说了啥?到底是怎么操作的?太优秀了!
看完这篇文章,以后面试别人或者被面试的过程中,遇到如何用栈实现一个队列的问题,那么就可以秀一波操作了。应该很少能有人在临场反应中能够答出来吧。
当然篇幅有点长,也有点绕脑子。就当做是繁忙工作之余的一个点心。接下来就开始品尝吧。
如何用两个栈实现一个队列呢?这是一个老生常谈的问题,为了扩充博文的长度我决定还是写一下过程。
比较笨的方法我就不说了( 一个栈作为缓冲栈,另一个储存数据,当出队列的时候,元素从一个栈倒出来,再倒回去。可真麻烦)
我们用两个栈分别代表一个队列的 尾部 tail 和一个队列的头部 head 。根据队列的特性,尾部栈只负责入队列操作,头部栈只负责出队列操作。
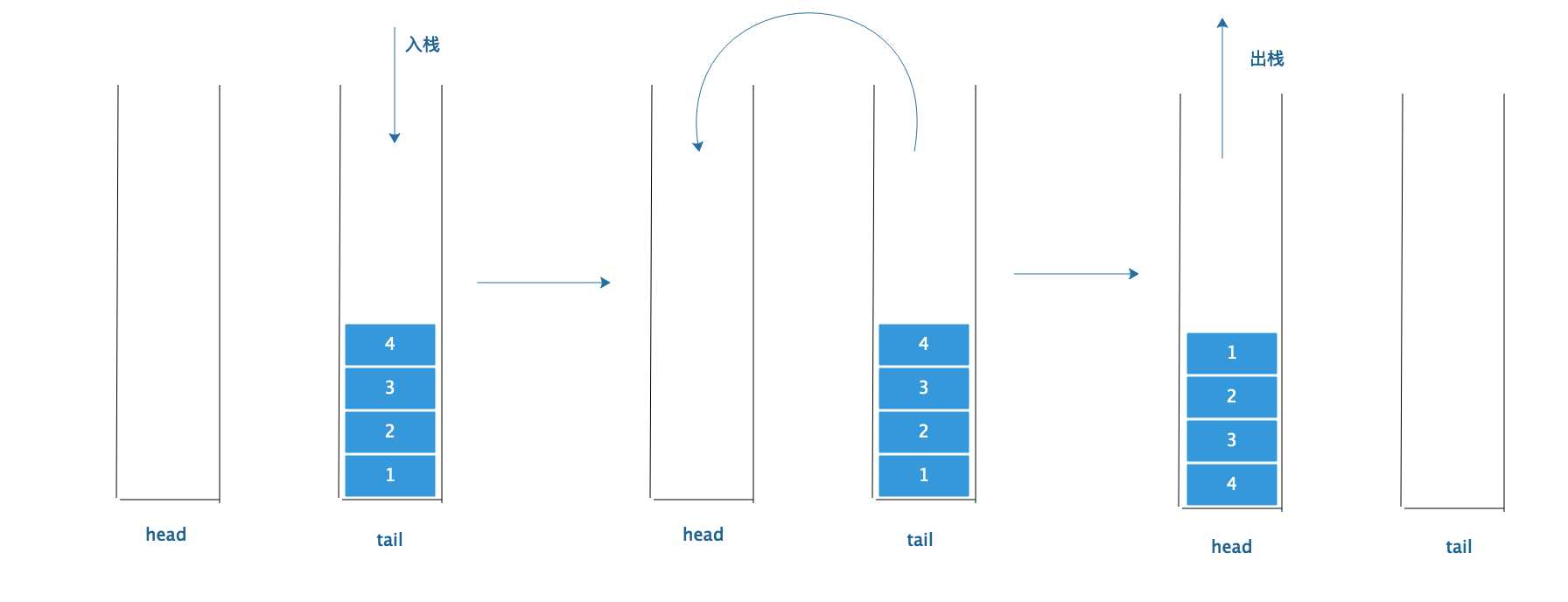
过程就如上图所示,当要出队列的时候,如果头部栈有元素,那么立刻出栈,效率O ( 1 )。
如果头部栈元素空了,就会把尾部栈的元素全部倒入头部栈中,再出栈。很显然倒元素的过程是一个O ( n )效率的操作,n是尾部栈里的元素个数。
出队列的效率就是O(n+1) (出队列操作也算上)而进栈都是O( 1 )的操作。
那么这样一个队列,它的效率高不高呢?
如果这样对队列进行操作:进队列 - 出队列 - 进队列 - 出队列 -进队列 ....
每次出队列效率是O (2) ,那n次出队列的效率就是 O ( 2 )+ O ( 2 ) + O( 2 )... => O( 2*n )
如果我这样操作:进队列 - 进队列 - 进队列 .... 出队列 出队列 出队列 ....
那么出n次队列的效率 是O( n+1 ) +O(1 )+O( 1 )+ ... => O( 2*n )
两种极端的情况下n次出队列的效率总的是 O (2*n) (别的情况下也是如此) 所以平均每次出队列的效率是O ( 2 ) !是常数效率!
这不就已经达到文章标题的要求了吗??对,是的,是我的题目不严谨。这道题目是源自于算法第四版的习题:
用有限个栈实现一个队列,保证每个队列(在最坏的情况下)都只需要常数次的栈操作
上面的方法在 最坏的情况下 是不满足的,也就是O(n+1)的那一次。
C# 中的 List 是怎么做到 Add 自动增加长度的呢?不是动态分配内存,而是当 List内部的array数组快满的时候 ,卡,一下直接复制一个二倍长度的array数组替换之前的数组,之后你再慢慢Add,直到再次堆满数组。相关操作可以查看List的源码
C# 中的 List 都可以这样操作,说明偶尔一次操作不是常数,并不影响整个数据结构的效率。可以平均一下(为啥平均要加粗,因为它是接下来的主要算法思想),相当于常数效率了。
所以上述栈模拟队列的操作完全合情合理,没什么不好的地方。不好的是这道习题,非要在最坏的地方也需要常数次操作。到这里其实这道题目已经不是优化效率的题目,也不是考验你的栈和队列的熟练程度,而是脑筋急转弯题。
就像之前所说的:
进队列 - 出队列 - 进队列 - 出队列 -进队列 ....
它完美的避开了那最坏的情况。因为它每次进队列之后都出队列,那么尾部栈里的元素就很少,这是不会出现O(n)操作的关键:确保尾部栈的元素时时刻刻都要最少,而头部栈的元素要最多
所以核心思路 就是:
将那次最坏情况下的 出队列的 倒元素的 O(n) 操作给平均到每次出入队列的操作中,确保尾部栈的元素时时刻刻都要比头部栈的元素少。
如果理解不了,也没关系,接下来会一步一步围绕这个思路去解决问题。
这是一个开始的双栈模拟一个队列的情况:
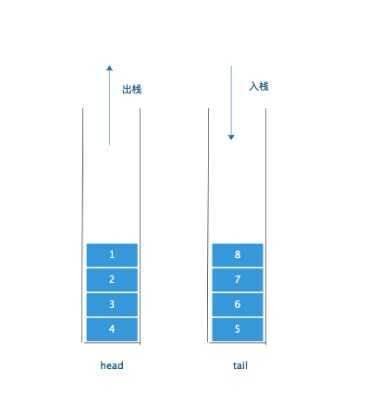
如果一直在出队列,刷刷几下把头部栈的元素出光了,那么下一次出队列就是最坏的情况了。
要做到尾部栈时时刻刻都在往头部栈里倒元素,需要引入另一个头部栈的副本 :head-l ,两个头部栈属于双胞胎关系。
在出队列的同时,我们把尾部栈的元素同时倒入头部栈副本中,当头部栈的元素出光了,下次出队列时只要交换头部栈和头部栈副本,就可以完美的衔接起来,避免了最坏情况的发生。
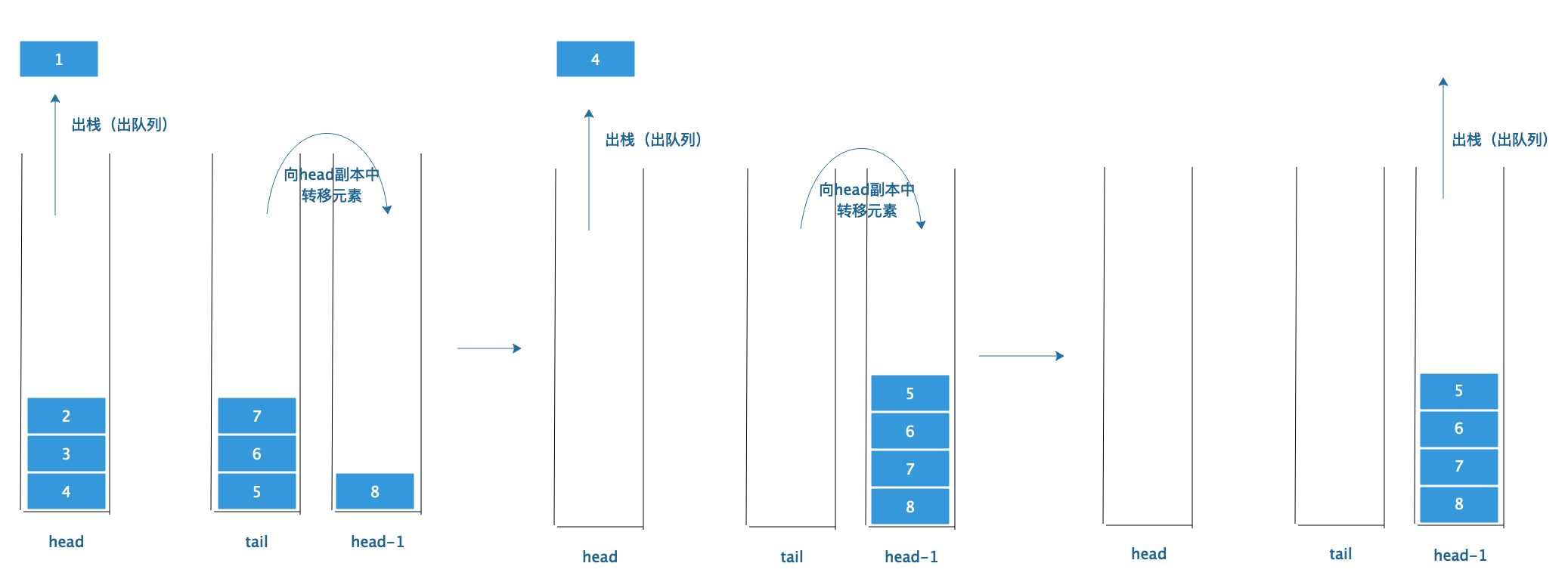
细心的同学应该发现了,如果在上述过程中,突然进队列怎么办呢?尾部栈突然进队列,那么就不能再往头部栈副本中倒元素了。既然有头部栈副本,那么也可以有一个尾部栈副本 :tail-l
进队列往尾部栈副本中放元素。此时进出队列的栈为 :tail-l 和head
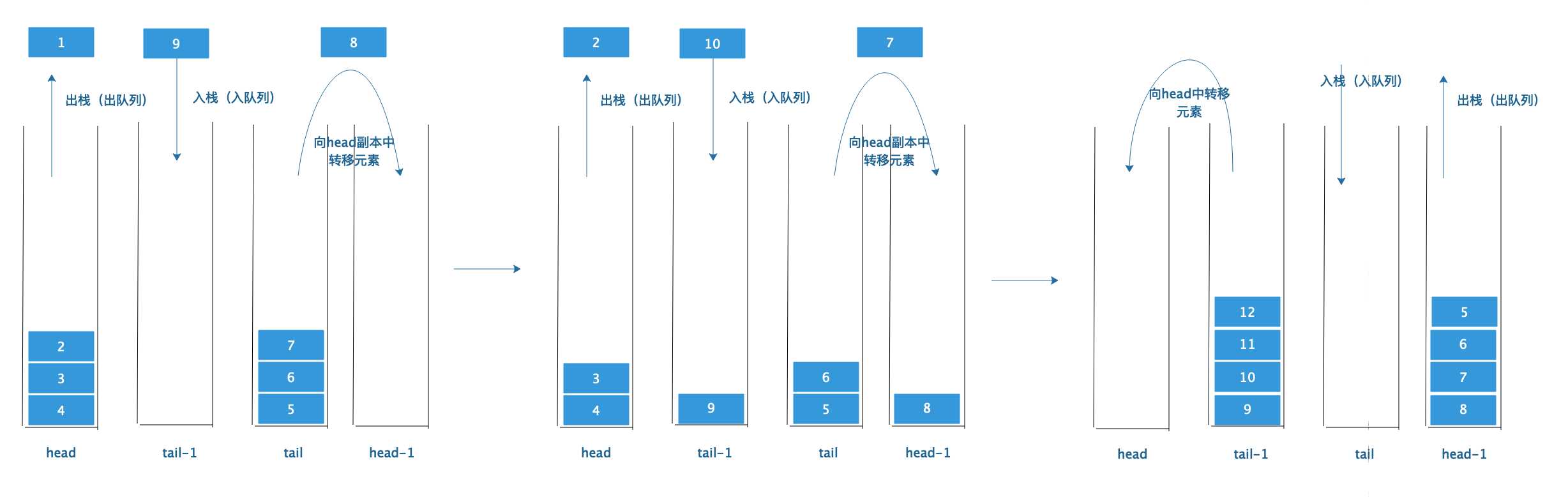
等到头部栈放空了,尾部栈倒空了,此时转换角色。出队列在head-l,入队列在tail。 而倒元素是从tail-l往head中倒元素
到这里,应该窥见了这样操作的中心思想:疯狂的,一刻不停歇的让tail中的元素进入head中,总是保持tail中的元素少于head中的元素
四个栈完美的实现了队列中出队列操作始终在常数效率。那么问题是不是就解决了呢?很显然没有,到这里才是一半。
接下来,随着栈的数量增多,请一定要保持头脑清醒,对栈有着深刻和正确的认识。
如果在上述过程中,不出队列,一个元素也不出,而是疯狂进队列呢?
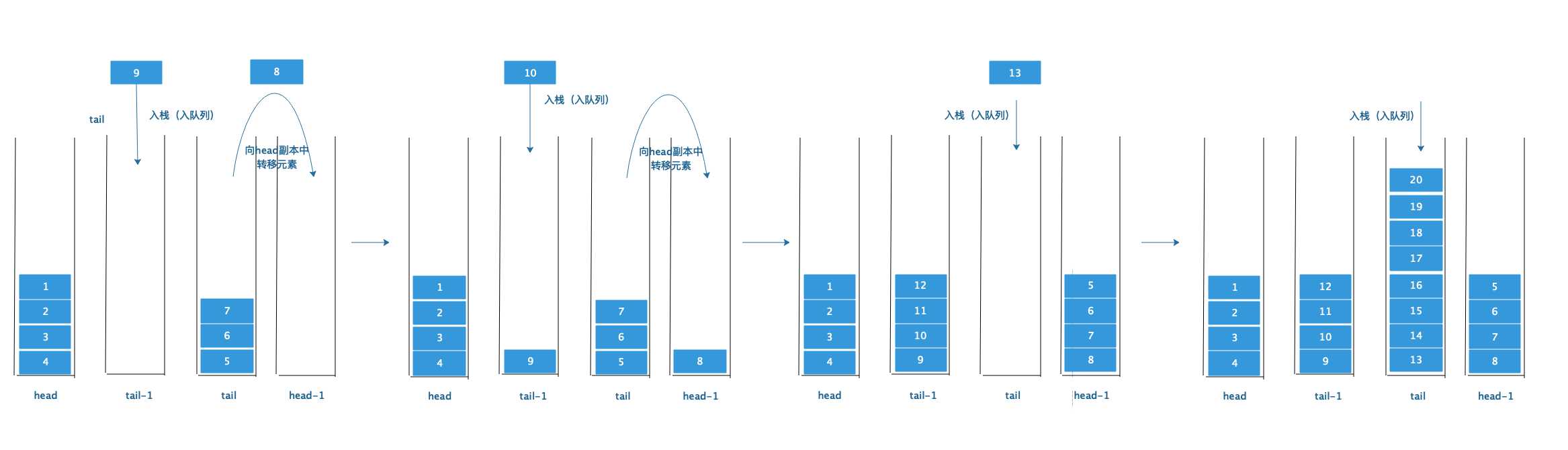
上图的过程是:在tail-l中入队列,当tail中元素倒空了,便交换角色,tail属于入队列的栈。(原则一:入队列时,哪个尾部栈谁是空的,谁就作为入队列栈,这样方便我们用代码实现)
与此同时一个元素也不出队列。所以最终导致的结果是tail中的元素老多了,老高了。那么会导致啥后果呢?从现在看来,出队列照样可以O(1)啊,如果聪明一点的同学应该会预料到会发生这样的情况:一直出队列的话
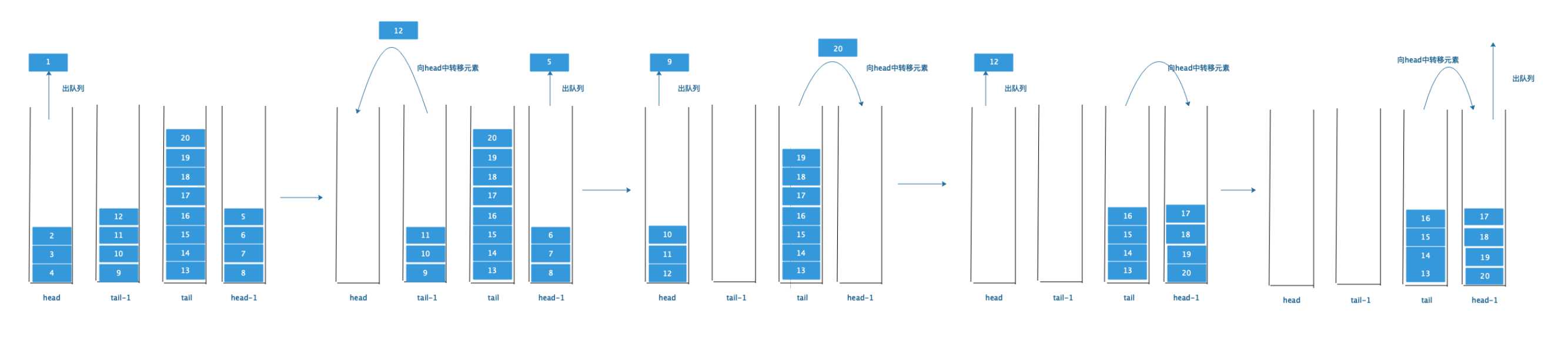
上图的过程:先从head中出队列,当head中元素出完了,便交换角色,head-l 出队列。与此同时,tail-l向已经空的head中倒元素(原则二:当某个头部栈为空时,那么尾部栈副本应该向这个头部栈转移元素,这里的尾部栈副本不一定就是tail-l,也可以是tail,因为它们二者是交换角色的关系)
同理head-l元素出完了,又和head交换角色,根据原则二,tail中的元素需要向head-l中倒元素。直到head出队列出空了。
此时按道理应该head-l和head交换角色,但这个时候却发现tail栈中的元素没倒完啊,元素13 还压在箱底呢!怎么办呢?一次性倒完吧!可是这又违背了常数操作的规定啊。谁知道tail栈中剩的元素会是多少个呢?
为了解决这个问题,再引入一个头部栈副本二:head-r ,这个栈专门用来让head去倒元素进去,为什么要这样做呢?看图就知道了,上下两个图是衔接的关系。
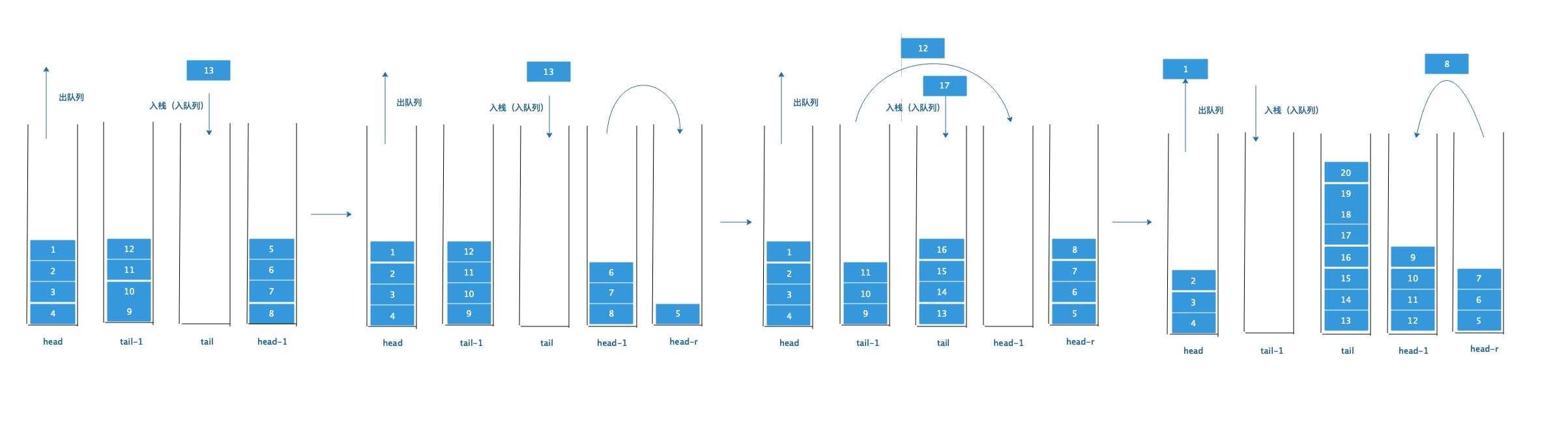
我们选取 疯狂进队列时的情况,加入head-r, 在往tail中进队列的时候,head-l往head-r中倒元素。 当没有head-r时,由于没有出队列,所有的头部栈的元素都原封不动,但因为了有了head-r,那么head-l就会倒空,那么根据原则二, tail-l就需要往head-l中倒元素。
tail-l倒空之后,head-r的元素再倒回head-l中,于是便得到最后一个张图:tail 和head-l中的元素是一样多的,所以无论怎么出队列都不会出现tail栈中的元素没倒完的情况。
所以引入head-r后,又多了一个原则三:当head-r为空时,需要从head栈中倒元素到head-r中
所以head-r就是为了缓解头部栈元素原封不动的情况,让尾部栈元素可以流动起来。
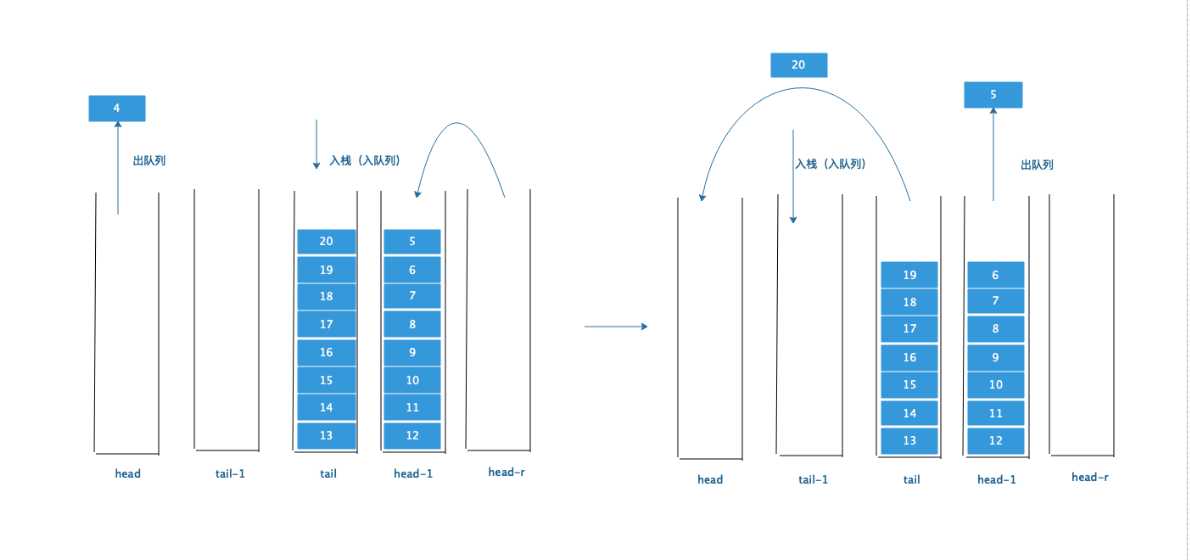
根据原则三:上面图的最后一个应该是这样的情况
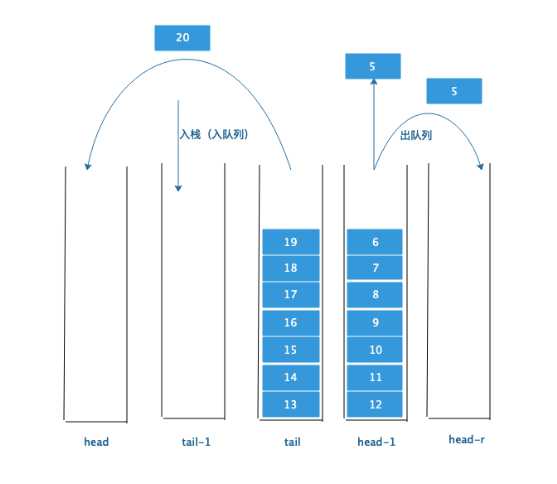
同时出队列和转移元素,这样就很尴尬了!!怎么办呢?再来一个栈!(栈多随便用,别搞出n个栈就可以)
这个栈是头部栈副本三号!叫做head-c ,它是专门的一个临时栈,相当于 当前处于出队列 状态的头部栈的引用。 出队列的操作都从head-c中实现,而代码实现其实可以用很巧妙的方法:一个栈,两个游标,分别代表自身和head-c
所以下图中名义上是head-l在出队列,实际上是head-c在出队列
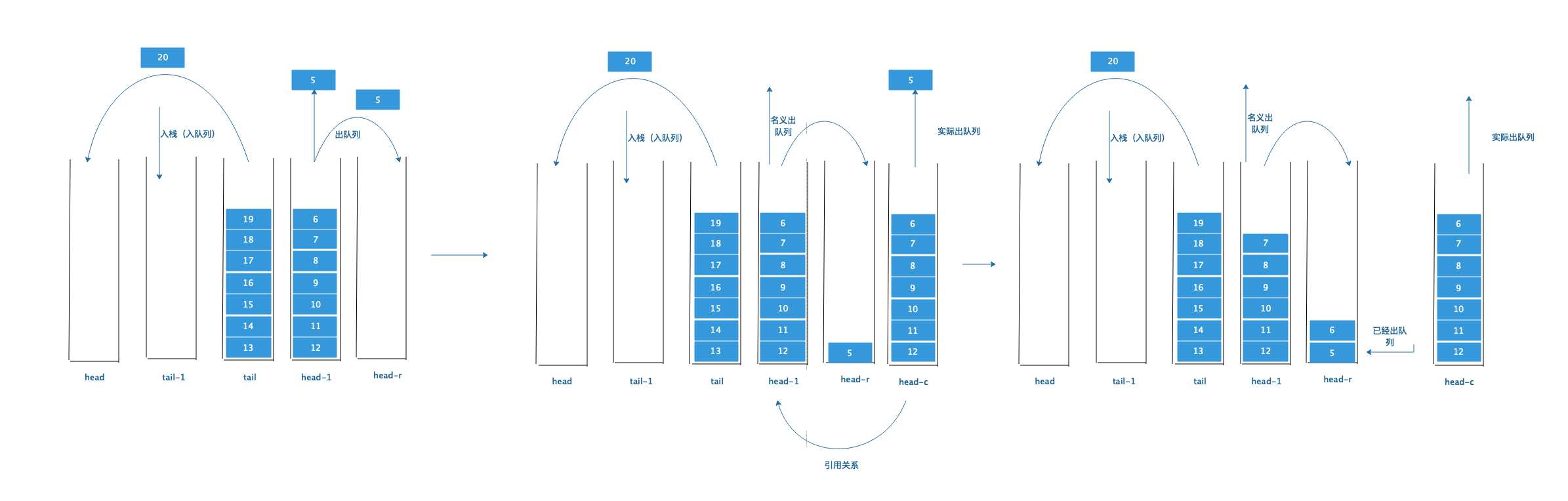
此外还有一点,在head-c中出队列,就需要在head-r中标记出来。下次head-r需要倒元素的时候,就要注意标记的元素已经被出队列了。
c++: 根据上文中的三个原则,以及一个栈,两个游标,再注意标记出队列元素。就可以很容易实现代码了。
c++ 有指针,指来指去,就更方便了。
#include <iostream>
#include <stdio.h>
#include <math.h>
#include <algorithm>
using namespace std;
struct StackHead
{
int s[1005];
int top=0;
int top_c=0;
};
struct Stack
{
int s[1005];
int top=0;
int dequeue=0;
};
class Queue
{
public:
int num;
StackHead* head;
StackHead* head_l;
Stack* tail;
Stack* tail_l;
Stack* head_r;
Queue();
void Enqueue(int number);
int Dequeue();
private:
int copy_tail;
int copy_head;
void Judge();
void Copy();
void Change();
};
Queue::Queue()
{
head = new StackHead;
head_l = new StackHead;
tail = new Stack;
tail_l = new Stack;
head_r = new Stack;
copy_head=0;
copy_tail=0;
num=0;
}
void Queue::Change()
{
if(tail_l->top==0)
{
Stack* temp = tail;
tail = tail_l;
tail_l = temp;
}
}
int Queue::Dequeue()
{
int res = head->s[--head->top];
head_r->dequeue++;
Change();
Copy();
return res;
}
void Queue::Enqueue(int number)
{
tail->s[tail->top++]=number;
Change();
num++;
Copy();
}
void Queue::Judge()
{
if(copy_tail==0&&tail_l->top>0&&head_l->top==0&&head_l->top_c==0) copy_tail=1;
if(copy_tail==1&&tail_l->top==0) copy_tail=0;
if(copy_head==0&&head->top_c>0) copy_head=1;
if(copy_head==1&&head->top_c==0) copy_head=0;
}
void Queue::Copy()
{
Judge();
if(copy_tail==1)
{
head_l->s[head_l->top++] = tail_l->s[--tail_l->top];
head_l->top_c++;
}
if(copy_head==1)
{
head_r->s[head_r->top++] = head->s[--head->top_c];
}
Judge();
if(copy_head==0&©_tail==0)
{
if(head_r->top > head_r->dequeue)
{
head_l->s[head_l->top++]=head_r->s[--head_r->top];
head_l->top_c++;
}
if(head_r->top == head_r->dequeue)
{
head_r->top=0;
head_r->dequeue=0;
head->top_c=0;
head->top=0;
StackHead* temp = head;
head = head_l;
head_l = temp;
}
}
}
int main()
{
Queue s = Queue();
}
理论上用了6个栈,实际上用了5个栈。
其实这个问题在实际中的应用中并没什么用。偶尔一次的O(n)效率的操作也无伤大雅,在大多数情况下。但是如果你遇到了无法承受任何一次O(n)操作的情况下,就可以想想如何把O(n)的操作给平均到每一步的操作中。
此外,偷梁换柱在上述过程也运用的炉火纯青。
最后,我们认为很简单的问题,往往深究下去,或者升级一下,会给我们带来更多。
https://stackoverflow.com/questions/5538192/how-to-implement-a-queue-with-three-stacks
标签:算法 中心 代码 htm 题目 情况下 经典 gen --
原文地址:https://www.cnblogs.com/dacc123/p/10574939.html