@省选模拟赛03/16 - T3@ 超级树

标签：for   简单   can   input   超级   output   amp   print   class   

@description@

一棵 k-超级树(k-SuperTree) 可按如下方法得到：取一棵深度为 k 的满二叉树，对每个节点向它的所有祖先连边（如果这条边不存在的话）。

例如，下面是一个 4-超级树：

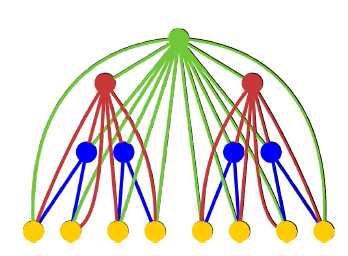
请统计一棵 k-超级树 中有多少条不同的简单有向路径，对 mod 取模。

input
一行两整数 k, mod。
output
一行一整数表示答案。

example
input1: 2 100
output1: 9

input2: 3 1000
output2: 245

input3: 20 998244353
output3: 450500168

explain
第一个样例的 9 条路径如下：
1, 2, 3, 1->2, 2->1, 1->3, 3->1, 2->1->3, 3->1->2。

@solution@

神仙树。

你问我为什么 3/27 要写 3/16 的模拟赛题解？
因为我热爱文化课。
题解就少说点，我要去准备月考了。

对于某一条路径：
要么它完全在左右某一棵子树中，可以转换为子问题；
要么它肯定经过根节点，这种情况再分成几类：
（1）只包含根节点。easy。
（2）以根节点作为终点/起点。easy。
（3）从左子树/右子树到另一颗子树。easy。
（4）从左子树/右子树回到这棵子树。……

好像第 4 类不可做的样子。我们需要求解一棵子树含有两条不相交路径的方案数。

既然如此，就再加一维状态。定义 dp(i, j) 表示深度为 i 的超级树选出 j 条不相交路径的方案数。
因为增加一个根节点最多只会将两条路径合并，即总路径数减一，故 j ≤ k。

然后就是非常简单的 O(n^3) 的 dp 题了。
最后答案为 dp(k, 1)。

@accepted code@

#include<cstdio>
const int MAXN = 500 + 5;
int dp[MAXN][MAXN], k, mod;
inline int add(int a, int b) {return (a + b) % mod;}
inline int mul(int a, int b) {return 1LL * a * b % mod;}
int main() {
    scanf("%d%d", &k, &mod); dp[0][0] = 1;
    for(int i=1;i<=k;i++)
        for(int p=0;p<=k;p++) {
            if( dp[i - 1][p] == 0 ) continue; 
            for(int q=0;q<=k;q++) {
                if( dp[i - 1][q] == 0 ) continue;
                int x = mul(dp[i - 1][p], dp[i - 1][q]);
                dp[i][p + q] = add(dp[i][p + q], mul(x, add(1, mul(2, add(p, q)))));
                dp[i][p + q - 1] = add(dp[i][p + q - 1], mul(x, add(mul(2, mul(p, q)), add(mul(p, p - 1), mul(q, q - 1)))));
                dp[i][p + q + 1] = add(dp[i][p + q + 1], x);
            }
        }
    printf("%d\n", dp[k][1]);
}//本地卡常，还没卡过。因此仅供参考。

@details@

暴力加一维状态的神仙操作。

写到一半我突然明白为什么要求是有向的路径……路径数变为原先的两倍，就不用求 2 的逆元。
出题人真懒。

@省选模拟赛03/16 - T3@ 超级树

标签：for   简单   can   input   超级   output   amp   print   class   

原文地址：https://www.cnblogs.com/Tiw-Air-OAO/p/10607000.html