标签:元素 design ima 输入 and put 博客 for The
四则运算2.1升级版(python)
源代码已上传至:https://github.com/lkx1237/-2.1/new/master
PSP
|
PSP2.1 |
Personal Software Process Stage |
预估时间(分钟) |
实际耗时(分钟) |
|
Planning |
计划 |
10 |
10 |
|
Estimate |
估计这个任务需要多少时间 |
1440 |
920 |
|
Development |
开发 |
700 |
200 |
|
Analysis |
需求分析(包括学习新技术) |
180 |
240 |
|
Design Spec |
生成设计文档 |
5 |
5 |
|
Design Review |
设计复审 |
10 |
15 |
|
Coding Standard |
代码规范 |
5 |
5 |
|
Design |
具体设计 |
40 |
60 |
|
Coding |
具体编码 |
300 |
380 |
|
Code Review |
代码复审 |
30 |
30 |
|
Test |
测试(自我测试,修改代码,提交修改) |
30 |
30 |
|
Reporting |
报告 |
120 |
120 |
|
Test Report |
测试+博客 |
120 |
120 |
|
Size Mearsurement |
计算工作量 |
10 |
10 |
|
Postmortem&Process Improvement Plan |
事后总结,并提出过程改进计划 |
40 |
50 |
|
合计 |
|
3040 |
2195 |
题目要求:
1.能自动生成小学四则运算题目
2.除了整数外,还要支持真分数的四则运算
3.除了以上的基本需求,还有
4.生成的算式长度随机
5.能处理分数的运算,结果能用分数(字符串类型)表示出来,能与用户输入相对应
解题思路:
1.定义一个函数用于随机生成随机长度的算式
2.把字符串型的算式转换为逆波兰式(RPN,也称后缀表达式)
3.再把后缀表达式利用栈结构计算出结果
4.最后再与用户的输入做比较
重点难点:
1.分数的表示与计算
2.后缀表达式的生成和计算
3.结果为负数的情况
具体程序设计:
成员变量
|
成员名 |
类型 |
功能 |
|
op |
list |
存放运算符 |
|
quest |
str |
存放算式 |
|
lens |
int |
2到9的随机长度 |
|
teop |
str |
存放当前运算符 |
|
tstr |
str |
存放当前算式 |
|
tint |
int |
存放当前运算数 |
成员函数
|
函数名 |
输入 |
输出 |
依赖函数 |
功能 |
|
get_string |
冇 |
字符串 |
冇 |
随机生成一个算式 |
|
get_ans |
str |
返回布尔类型 |
get_string |
将用户输入与正确答案比较 |
|
to_rpn |
str |
返回后缀表达式 |
get_ans |
将随机生成的算式转换为RPN |
|
this_bigger |
str,str |
返回布尔表达式 |
冇啊 |
比较两个运算符的优先级 |
|
slove_rpn |
str |
返回计算结果 |
get_ans |
将后缀表达式计算出来 |
核心代码:
随机生成一个算式
def get_string(self): self.lens = random.randint(2, 9) self.teop = ‘‘ self.tstr = [] for i in range(self.lens): if self.teop == ‘÷‘: self.tint = random.randint(1, 8) self.teop = random.choice(self.op) elif self.teop == ‘/‘: self.tint = random.randint(self.tint+1, 9) self.teop = random.choice(self.op[:-1]) else: self.tint = random.randint(0, 8) self.teop = random.choice(self.op) self.tstr.append(str(self.tint)) self.tstr.append(self.teop) self.tstr[-1] = ‘=‘ self.tstr = ‘‘.join(self.tstr) self.quest = self.tstr return self.tstr def get_ans(self, quest): rpn = self.to_rpn(quest[:-1]) the_ans = self.slove_rpn(rpn) print(‘问题如下:‘, self.quest) my_ans = input() print(‘结果为‘, str(the_ans)) if str(the_ans) == my_ans : print(‘right!‘) return True else: print(‘wrong...‘) return False
将随机生成转换为RPN
def to_rpn(self, ques): #Reverse Polish notation self.stack = [] s = ‘‘ for x in ques: if x != ‘+‘ and x != ‘-‘ and x != ‘ב and x != ‘÷‘ and x != ‘/‘: s += x #若为数字,直接输出 else: # 若为运算符,进栈 if not self.stack: #栈空 self.stack.append(x) else: if self.this_bigger(x, self.stack[-1]): #运算级高于栈顶元素 self.stack.append(x) #直接进栈 else: while self.stack: if self.this_bigger(x, self.stack[-1]): break s += self.stack.pop() self.stack.append(x) while self.stack: s += self.stack.pop() # print(‘在to_rpn函数中,rpn:‘,s) return s
将后续表达式计算出来
def slove_rpn(self, rpn): #print(‘进入slove_rpn函数:‘) self.stack1 = [] #用于保存运算数 for x in rpn: if x != ‘+‘ and x != ‘-‘ and x != ‘ב and x != ‘÷‘ and x != ‘/‘: self.stack1.append(int(x)) elif x == ‘+‘: second = self.stack1.pop() first = self.stack1.pop() self.stack1.append(first + second) elif x == ‘-‘: second = self.stack1.pop() first = self.stack1.pop() self.stack1.append(first - second) elif x == ‘ב: second = self.stack1.pop() first = self.stack1.pop() self.stack1.append(first * second) elif x == ‘÷‘: second = self.stack1.pop() first = self.stack1.pop() self.stack1.append(Fraction(first, second)) elif x == ‘/‘: second = self.stack1.pop() first = self.stack1.pop() self.stack1.append(Fraction(first, second)) resault = self.stack1[0] if resault >= 0: #print(‘--------------题结束----------------‘) return resault elif resault < 0: #print(‘结果为负数!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!‘) s = self.get_string() rpn = self.to_rpn(s[:-1]) return self.slove_rpn(rpn)
运行效果:

效能分析:
用profiler进行效能分析:
import profile
if __name__=="__main__":
profile.run("main()")
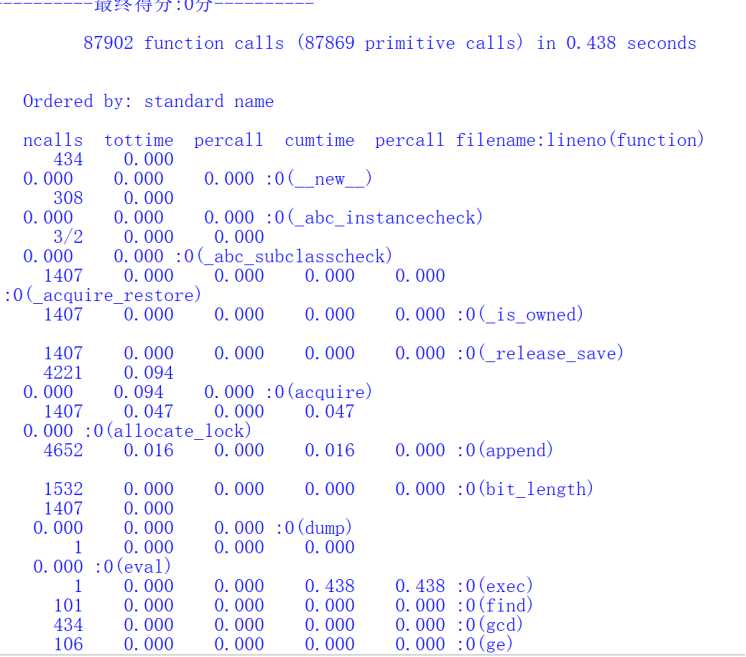
效能分析结果如下 :
运行次数为100次,所用时间长度为0.438s
2.1版四则运算总结:
2.1版与2.0版相比,从功能上2.1版可以进行带括号的综合运算,而2.0版只能进行两位数字的简单综合运算,优化了程序运行速度.
标签:元素 design ima 输入 and put 博客 for The
原文地址:https://www.cnblogs.com/lkx1237/p/10617417.html