标签：int abs 相同 变化 信号 扩展 算法 tail pre
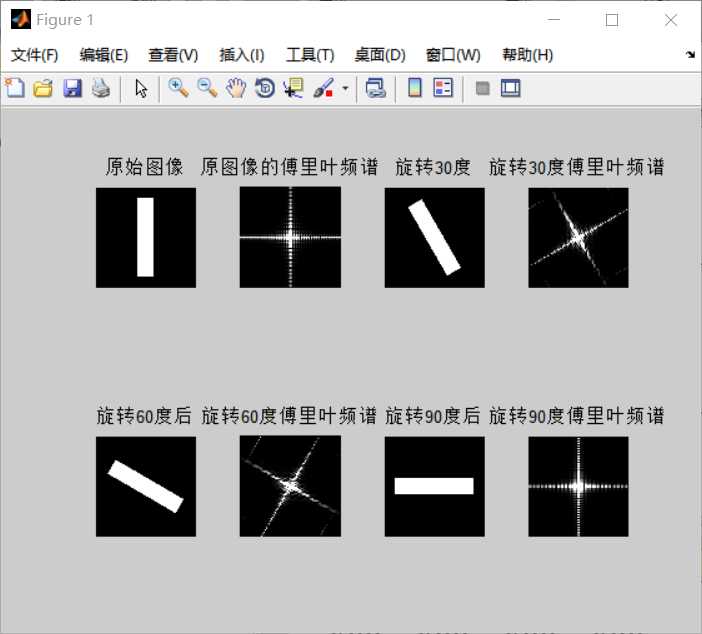
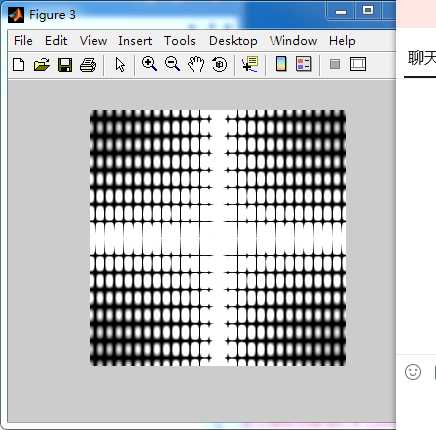
1旋转图像，并显示图像的傅里叶频谱
1 I=zeros(256,256); 2 I(28:228,108:148)=1; 3 subplot(2,4,1); 4 imshow(I); 5 title(‘原始图像‘); 6 J=fft2(I);%对信号进行快速Fourier变换，注释一 7 F=abs(J);%求得Fourier变换后的振幅，注释二 8 J1=fftshift(F)%注释三 9 subplot(2,4,2); 10 imshow(J1,[5 50]) 11 title(‘原图像的傅里叶频谱‘); 12 J=imrotate(I,30,‘bilinear‘,‘crop‘);%逆时针旋转30度，注释四 13 subplot(2,4,3); 14 imshow(J); 15 title(‘旋转30度‘); 16 J1=fft2(J); 17 F=abs(J1); 18 J2=fftshift(F); 19 subplot(2,4,4) 20 imshow(J2,[5 50]) 21 title(‘旋转30度傅里叶频谱‘); 22 J=imrotate(I,60,‘bilinear‘,‘crop‘);%逆时针旋转60度 23 subplot(2,4,5); 24 imshow(J); 25 title(‘旋转60度后‘); 26 J1=fft2(J); 27 F=abs(J1); 28 J2=fftshift(F); 29 subplot(2,4,6) 30 imshow(J2,[5 50]) 31 title(‘旋转60度傅里叶频谱‘); 32 J=imrotate(I,90,‘bilinear‘,‘crop‘);%逆时针旋转90度 33 subplot(2,4,7); 34 imshow(J); 35 title(‘旋转90度后‘); 36 J1=fft2(J); 37 F=abs(J1); 38 J2=fftshift(F); 39 subplot(2,4,8) 40 imshow(J2,[5 50]) 41 title(‘旋转90度傅里叶频谱‘);
2二维余弦正反变换
1 I=imread(‘C:\\Users\\Administrator\\Desktop\\lenagray.jpg‘); 2 subplot(1,3,1) 3 imshow(I); 4 title(‘原始图像‘) 5 J=dct2(I); 6 subplot(1,3,2) 7 imshow(log(abs(J)),[]); 8 title(‘余弦变换系数‘); 9 k=idct2(J)/255; 10 subplot(133); 11 imshow(k); 12 title(‘余弦反变换恢复图像‘);
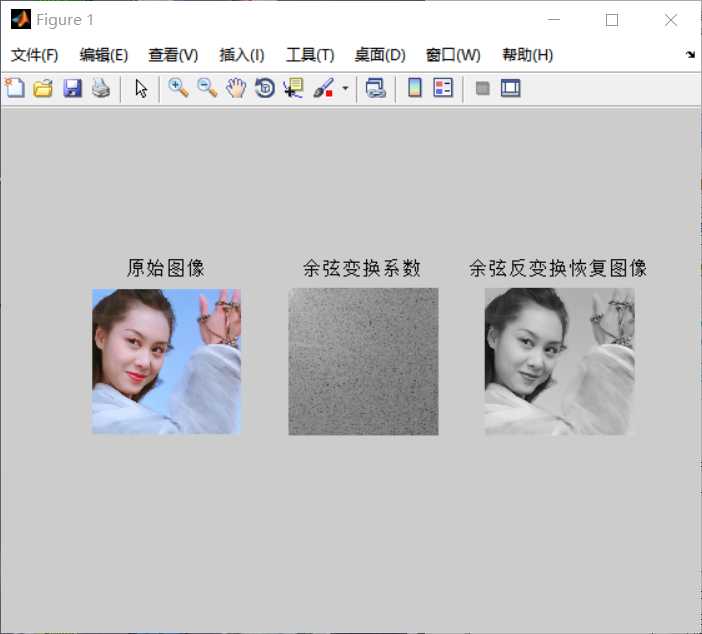
3尺度变化
1 I=zeros(256,256); 2 I(8:248,110:136)=255; 3 figure(1); 4 imshow(I); 5 J3=fft2(I); 6 F2=abs(J3); 7 F3=fftshift(F2); 8 figure(2); 9 imshow(F3,[5 30]); 10 a=0.1; 11 12 for i=1:256 13 for j=1:256; 14 I(i,j)=I(i,j)*a; 15 end 16 end 17 J2=fft2(I); 18 F1=abs(J2); 19 J3=fftshift(F1); 20 figure(3); 21 imshow(J3,[5 30])
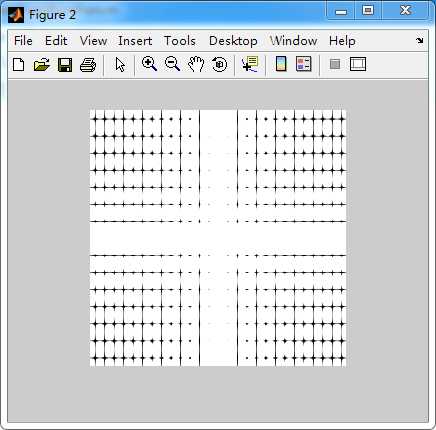
当f(x,y)在水平方向进行扩展，相同间隔下频谱中u方向零点的数量也增加
4傅里叶变换实例
1 I=imread(‘D:/picture/lenagray.jpg‘); 2 figure;imshow(I); 3 p=fft2(I); 4 p=fftshift(p); 5 figure;imshow(log(abs(p)),[8 10]); 6 I1=imnoise(I,‘gaussian‘,0,0.01); 7 figure;imshow(I1); 8 p1=fft2(I); 9 p1=fftshift(p1); 10 figure;imshow(log(abs(p1)),[8 10]);
F[PQDON~MXO_JCN5(TI.png)
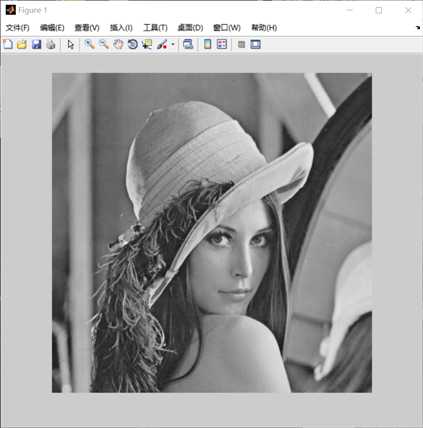
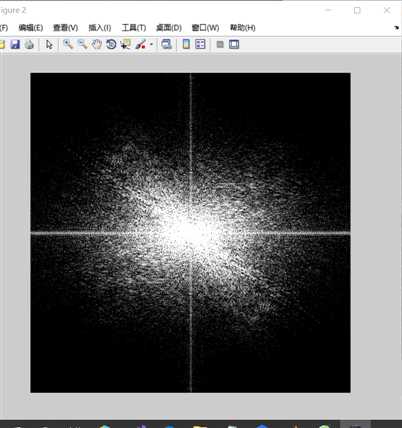
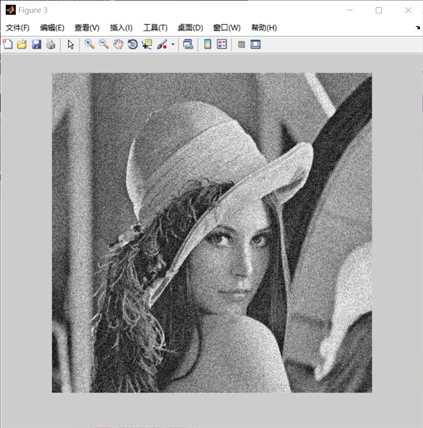
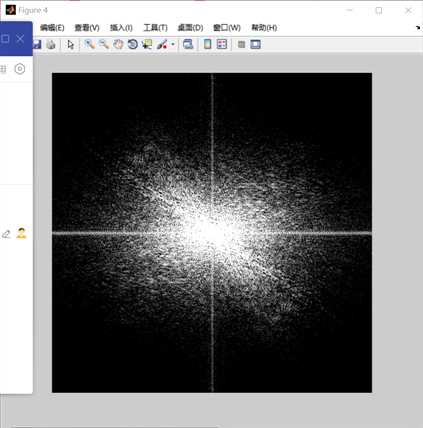
figure1是原图figure2是原图的傅里叶频谱图（已经移中），
figure3是加了高斯噪声的lena图，及其对应的频谱图。
有一些关于频谱图的结论：中心白色区域是低频，但能量高，幅角大，中心之外的区域是黑色区域，对应的是高频，能量幅度小，
对于图像灰度变化缓慢的区域，对应它变换后的低频分量部分；图像灰度呈阶跃变换的区域，对应变换后的高频部分。除颗粒噪声外，图像细节的边缘、轮廓处都是灰度变化突出区域。他们都具有变换后的高频分量特征。我个人观点是图像的灰度值越小即越黑则对应的频谱中心区域越小，高频成分占的比重越高。
具体关于频谱的内容可以看一下这两篇博客
https://blog.csdn.net/Struggle_For_M/article/details/51207370%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
注释一：
??1. Y = fft（y）;
2. Y = fft（y，N）;
式中，y是序列，Y是序列的快速傅里叶变换。y可以是一向量或矩阵，若y为向量，则Y是y的FFT，并且与y具有相同的长度。若y为一矩阵，则Y是对矩阵的每一列向量进行FFT。
注释二：
注释三：
fft是一维傅里叶变换，即将时域信号转换为频域信号fftshift是针对频域的，将FFT的DC分量移到频谱中心
即对频域的图像，（假设用一条水平线和一条垂直线将频谱图分成四块）对这四块进行对角线的交换与反对角线的交换
fft：对模拟信号进行变换，变换结果是左右对称的，有负频率，如下图（a）中的作图所示。
DFT的求和区间是0~N-1,DFT的物理意义是对fft的结果等间隔的采样N点，但是人为的规定0~N-1使得只采样了正频率，和fft结果不一致。由于fft的对称性或者说是周期性（见（b）的右图），所以可以以DFT结果以Fs/2为中心， 把Fs/2频率右半部分移到左半部分（即N/2~N-1）个点平移到负半轴，这样的结果的形状就同（a）中右面的图一致了，这也即是fftshift的原因。。其实是为了与fft结果一致。
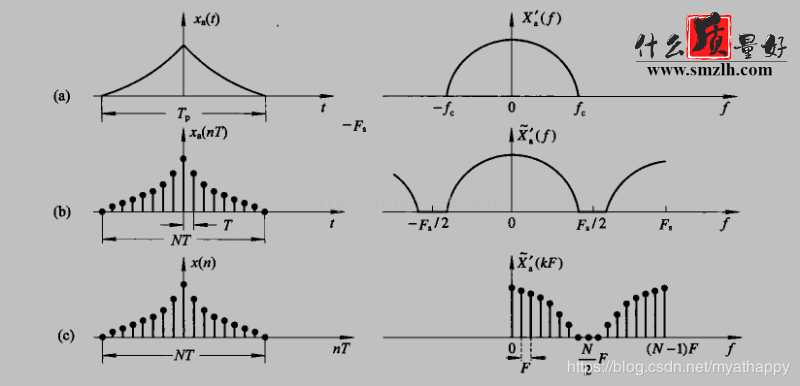
其他内容可参考：https://www.cnblogs.com/WHaoL/p/6595132.html
注释四：
标签：int abs 相同 变化 信号 扩展 算法 tail pre
原文地址：https://www.cnblogs.com/henuliulei/p/10578580.html
