标签:col include color 直接 opened 包含 string onclick 存在
eg:1-10的线段树(区间里面的数代表左右边界值,区间下面的数代表在tree数组中的下标)
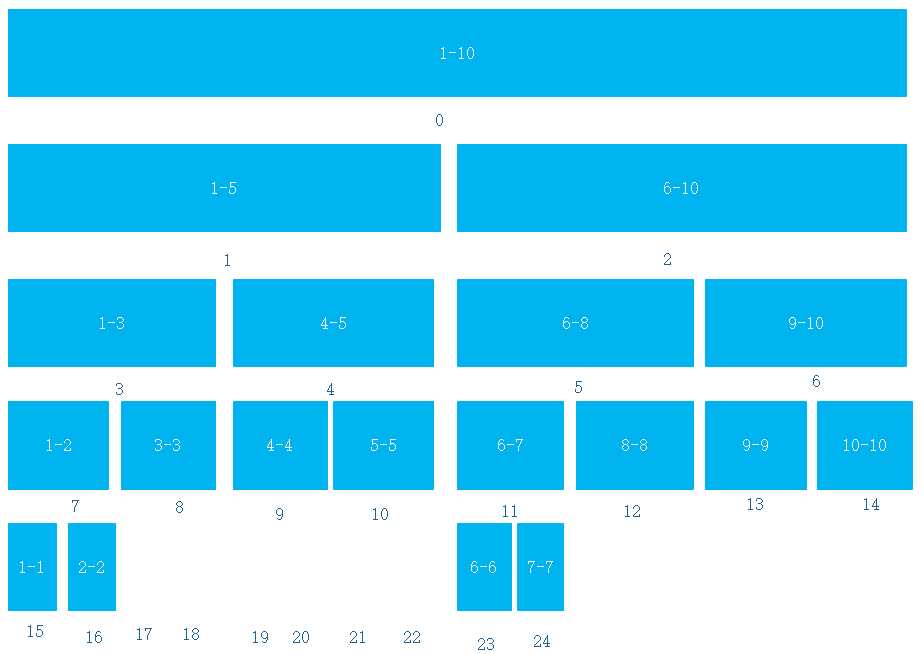
0.基础结构体
1 struct N 2 { 3 int l,r,w; //左边界 右边界 区间维护值 4 int lazy; //懒值 5 }tree[4*n];
注意:这里的tree要开4倍n的大小,原因是开的区间中有一些是没被利用的如上图.(懒值的作用下面会说)
1.建树-build函数
更新当前区间左右边界+叶子节点处理(赋值)+往左右子节点扩展+更新
eg:区间维护的值为区间和(l,r,k初始值分别为1,n,0)(k为区间下标)
1 void build(int l,int r,int k) 2 { 3 tree[k].l=l,tree[k].r=r;//更新当前区间左右边界 4 if(l==r) //叶子节点处理 5 { 6 scanf("%d",&tree[k].w); 7 return ; 8 } 9 int mid=(l+r)>>1; 10 build(l,mid,k*2+1); //扩展左子区间 11 build(mid+1,r,k*2+2); //扩展右子区间 12 tree[k].w=tree[2*k+1].w+tree[2*k+2].w; //更新 13 }
2.单点查询-ask_point函数
叶子区间处理(若到达叶子区间则找到值)+前进区间判断(该询问左子区间还是右子区间)
eg:区间维护的值为区间和(查询第x个值)
1 int ask_point(int k,int x) 2 { 3 if(tree[k].l==tree[k].r) return tree[k].w; //叶子节点处理 4 int mid=(tree[k].l+tree[k].r)>>1; //前进区间 5 if(x<=mid) return ask_point(k*2+1,x); 6 else return ask_point(k*2+2,x); 7 }
3.单点修改-add_point函数
单点查询+更新
eg:区间维护的值为区间和(第x个值加上y)
1 void add_point(int k,int x,int y) 2 { 3 if(tree[k].l==tree[k].r) //叶子区间处理 4 { 5 tree[k].w+=y; 6 return ; 7 } 8 int mid=(tree[k].l+tree[k].r)>>1; //前进区间 9 if(x<=mid) add_point(k*2+1,x,y); 10 else add_point(k*2+2,x,y); 11 tree[k].w=tree[k*2+1].w+tree[k*2+2].w; //更新 12 }
4.区间查询-ask_interval函数
被包含区间处理(若区间被包含则直接贡献该区间的值)+前进区间判断(需不需要收集左子区间和右子区间的值)
eg:区间维护的值为区间和(查询(a,b)区间的区间和)
1 int ask_interval(int k,int a,int b) 2 { 3 if(tree[k].l>=a&&tree[k].r<=b) return tree[k].w;//区间被包含 4 int mid=(tree[k].l+tree[k].r)>>1; 5 int sum=0; //用来收集左右子区间的值 6 if(a<=mid) sum+=ask_interval(k*2+1,a,b); 7 if(b>mid) sum+=ask_interval(k*2+2,a,b); 8 return sum; 9 }
5.区间修改-add_interval函数
这里需要增加一个新概念-懒值
当一个节点区间被要修改区间包含时,只需要改这个节点区间的值就行了,不需要往下修改子区间的值,当需要用到该区间的子区间时才去修改该区间的子区间的值.这个优化的实现就需要用到懒值,懒值存的是子区间需要修改的值的累积值,当需要用到子区间时就把懒值分配下去-down函数.
这里给出down函数写法(把懒值分配给子区间)
1 void down(int k) 2 { 3 tree[k*2+1].lazy+=tree[k].lazy; 4 tree[k*2+2].lazy+=tree[k].lazy; 5 tree[k*2+1].w+=tree[k].lazy*(tree[k*2+1].r-tree[k*2+1].l+1); 6 tree[k*2+2].w+=tree[k].lazy*(tree[k*2+2].r-tree[k*2+2].l+1); 7 tree[k].lazy=0; 8 }
add_interval函数写法是在区间查询的基础上加上了down函数的利用和更新代码
eg:区间维护的值为区间和(给(a,b)区间的值加上x)
1 void add_interval(int k,int a,int b,int x) 2 { 3 if(tree[k].l>=a&&tree[k].r<=b) 4 { 5 tree[k].w+=x*(tree[k].r-tree[k].l+1); 6 tree[k].lazy+=x; 7 return ; 8 } 9 if(tree[k].lazy) down(k); //如果到这一步则表明需要用到该节点子区间的值 10 int mid=(tree[k].l+tree[k].r)>>1; 11 if(a<=mid) add_interval(k*2+1,a,b,x); 12 if(b>mid) add_interval(k*2+2,a,b,x); 13 tree[k].w=tree[k*2+1].w+tree[k*2+2].w; 14 }
6.lazy引入的影响
前面所过当要用到用有lazy值的节点的子区间时,需要把lazy分配下去,所以引入lazy后除了build函数其他功能函数都必须追加一个判断 if(lazy存在) down(k);
下面给出具有以上5个基本功能的线段树代码(区间维护的值为区间和)

1 #include <cstdio> 2 #include <cmath> 3 #include <iostream> 4 #include <cstring> 5 #include <algorithm> 6 #include <vector> 7 #include <string> 8 #include <utility> 9 #include <queue> 10 #include <stack> 11 #include <map> 12 #include <set> 13 const int INF=0x3f3f3f3f; 14 using namespace std; 15 16 const int MAX_N=100000; 17 struct N 18 { 19 int l,r,w; 20 int lazy; 21 }tree[4*MAX_N]; 22 23 void build(int l,int r,int k) 24 { 25 tree[k].l=l,tree[k].r=r; 26 if(l==r) 27 { 28 scanf("%d",&tree[k].w); 29 return ; 30 } 31 int mid=(l+r)>>1; 32 build(l,mid,k*2+1); 33 build(mid+1,r,k*2+2); 34 tree[k].w=tree[2*k+1].w+tree[2*k+2].w; 35 } 36 37 void down(int k) 38 { 39 tree[k*2+1].lazy+=tree[k].lazy; 40 tree[k*2+2].lazy+=tree[k].lazy; 41 tree[k*2+1].w+=tree[k].lazy*(tree[k*2+1].r-tree[k*2+1].l+1); 42 tree[k*2+2].w+=tree[k].lazy*(tree[k*2+2].r-tree[k*2+2].l+1); 43 tree[k].lazy=0; 44 } 45 46 int ask_point(int k,int x) 47 { 48 if(tree[k].l==tree[k].r) return tree[k].w; 49 if(tree[k].lazy) down(k); //只添加了该判断 50 int mid=(tree[k].l+tree[k].r)>>1; 51 if(x<=mid) return ask_point(k*2+1,x); 52 else return ask_point(k*2+2,x); 53 } 54 55 void add_point(int k,int x,int y) 56 { 57 if(tree[k].l==tree[k].r) 58 { 59 tree[k].w+=y; 60 return ; 61 } 62 if(tree[k].lazy) down(k); //只添加了该判断 63 int mid=(tree[k].l+tree[k].r)>>1; 64 if(x<=mid) add_point(k*2+1,x,y); 65 else add_point(k*2+2,x,y); 66 tree[k].w=tree[k*2+1].w+tree[k*2+2].w; 67 } 68 69 int ask_interval(int k,int a,int b) 70 { 71 if(tree[k].l>=a&&tree[k].r<=b) return tree[k].w; 72 if(tree[k].lazy) down(k); //只添加了该判断 73 int mid=(tree[k].l+tree[k].r)>>1; 74 int sum=0; 75 if(a<=mid) sum+=ask_interval(k*2+1,a,b); 76 if(b>mid) sum+=ask_interval(k*2+2,a,b); 77 return sum; 78 } 79 80 void add_interval(int k,int a,int b,int x) 81 { 82 if(tree[k].l>=a&&tree[k].r<=b) 83 { 84 tree[k].w+=x*(tree[k].r-tree[k].l+1); 85 tree[k].lazy+=x; 86 return ; 87 } 88 if(tree[k].lazy) down(k); 89 int mid=(tree[k].l+tree[k].r)>>1; 90 if(a<=mid) add_interval(k*2+1,a,b,x); 91 if(b>mid) add_interval(k*2+2,a,b,x); 92 tree[k].w=tree[k*2+1].w+tree[k*2+2].w; 93 } 94 95 int main() 96 { 97 int n; 98 cin>>n; 99 build(1,n,0); 100 //该部分随题意添加 101 return 0; 102 }
标签:col include color 直接 opened 包含 string onclick 存在
原文地址:https://www.cnblogs.com/VBEL/p/10630435.html