标签:情况 申请 两种 初始 子串 ++ 字母 连续 alt
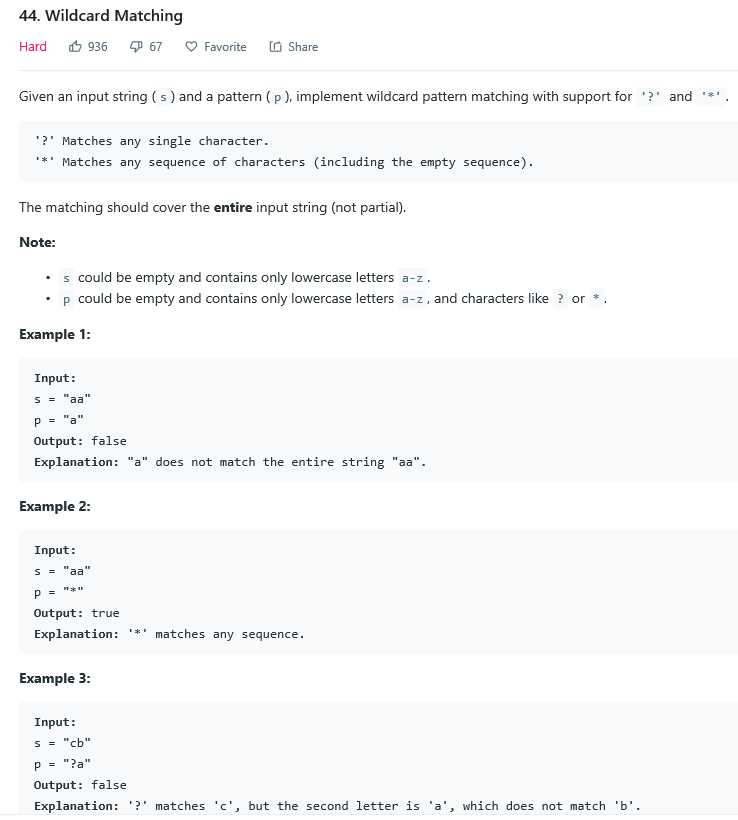

题意:s是空串或包含a-z字母;
p为包含a-z字母或?或 * (其中*可以匹配任意字符串包括空串,?可以匹配任意字符)。
思路:
1)特殊情况:当s为空串时,p为连续 * 时,则连续 * 的位置都为true。
2)若p的第j个字符为 * ,分两种情况:
a) 若p中的前 j-1个字符和 s 中的前 i 个字符匹配成功了, 即 dp[i][j-1] == true , 因为 * 可以匹配空串,则 dp[i][j] == true;
b) 若p中的前 j 个字符和 s 中前 i-1 个字符匹配成功了,即 dp[i-1][j] == true , 因为 * 可以匹配任意字符串,则 dp[i][j] == true.
3) 若p中的第j个字符不是 * 时,则需要满足 dp[i-1][j-1] == true 和 s 中的第i个字符和p中的第j个字符相等, 即 s[i-1] == p[j-1], 或者 p中的第j个字符是问号, 即 p[j-1] == ‘?‘ 则 dp[i][j] == true.
注意:dp[][] 初始化申请空间大小要为 (m+1, n+1) ,因为dp[0][0] 为p和s为空串时候的情况。
dp如果用二维数组定义会超时!所以用二维vector。
注:s[i-1] 代表s中第i位字符。
class Solution { public: bool isMatch(string s, string p) { int m = s.size(); int n = p.size(); //dp[i][j]:s中前i个字符组成的子串和p中前j个字符组成的子串是否能匹配 //bool dp[m+1][n+1] = {false}; vector<vector<bool> > dp(m+1, vector<bool>(n+1, false)); //s,p都为空,返回0 dp[0][0] = true; //s为空, p为连续星号时,赋值为true for(int i = 1; i <= n; i++){ if(p[i-1] == ‘*‘) dp[0][i] = dp[0][i-1]; } for(int i=1; i<=m; i++){ for(int j=1; j<=n; j++){ if(p[j-1] == ‘*‘) dp[i][j] = dp[i-1][j] || dp[i][j-1]; else dp[i][j] = (s[i-1]==p[j-1] || p[j-1] == ‘?‘) && dp[i-1][j-1]; } } return dp[m][n]; } };
标签:情况 申请 两种 初始 子串 ++ 字母 连续 alt
原文地址:https://www.cnblogs.com/Bella2017/p/10644299.html