标签:ane 怎样 dal lin 机器 count ade 预测 def
0.决策树
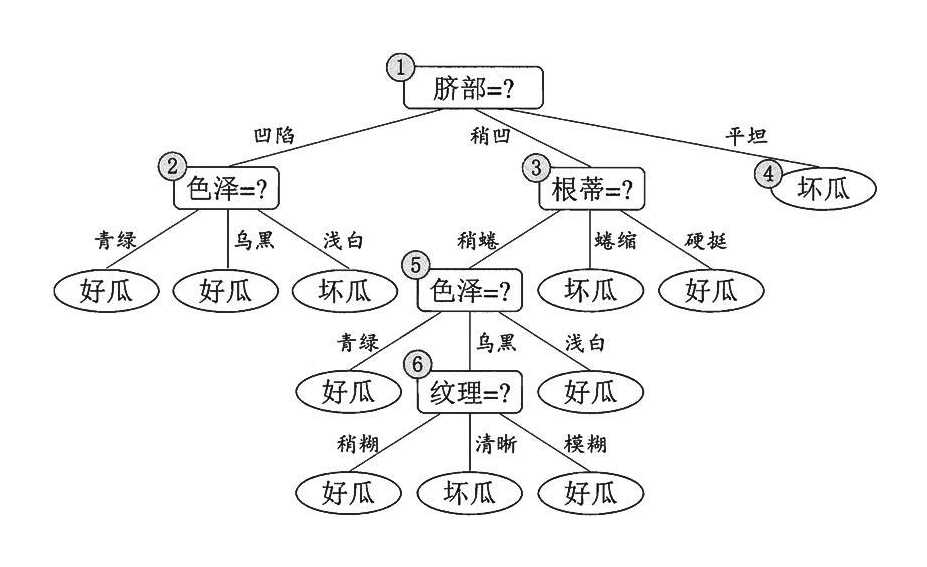
决策树是一种树型结构,其中每个内部节结点表示在一个属性上的测试,每一个分支代表一个测试输出,每个叶结点代表一种类别。
决策树学习是以实例为基础的归纳学习
决策树学习采用的是自顶向下的递归方法,其基本思想是以信息熵为度量构造一棵熵值下降最快的树。到叶子节点的处的熵值为零,此时每个叶结点中的实例都属于同一类。
1.决策树学习算法的特点
决策树算法的最大优点是可以自学习。在学习的过程中,不需要使用者了解过多知识背景,只需要对训练实例进行较好的标注,就能够进行学习了。
在决策树的算法中,建立决策树的关键,即在当前状态下选择哪个属性作为分类依据。根据不同的目标函数,建立决策树主要有一下三种算法:
主要的区别就是选择的目标函数不同,ID3使用的是信息增益,C4.5使用信息增益率,CART使用的是Gini系数。
2.信息熵
在信息论与概率统计中,熵(entropy)是表示随机变量不确定性的度量。设X是一个区有限个值的离散随机变量,其概率分布为:
则随机变量X的熵的定义为:
在上述式中,若pi=0,则定义0log0=0,通常,式中的对数以2为底或者以e为底(自然对数),这时熵的单位分别称作比特(bit)或者纳特(nat)。由定义可知,熵只依赖于X的分布,而与X的取值无关,所以也可以将X的熵记作H(p),即:
熵越大,随机变量的不确定性就越大。从定义可以验证
当随机变量确定时,熵的值最小为0,当熵值最大时,随机变量不确定性最大。
设有随机变量(X,Y),其联合概率分布为
条件熵H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性,随机变量X给定的条件下随机变量Y的条件熵H(Y|X),定义为X给定条件下Y的条件概率分布的熵对X的数学期望:
这里,pi=P(X=xi),i=1,2,......,n
当熵和条件熵中的概率是有数据估计(极大似然估计)得到时,所对应的熵与条件熵分别称为经验熵和条件经验熵。此时,如果有0概率,则令0log0=0.
信息增益表示得知特征X的信息而使得类Y的信息的不确定性减少的程度。
特征A对数据集D的信息增益g(D,A),定义为集合D的经验熵H(D)与特征A的经验条件熵H(D|A)之差,即:
一般地,熵H(Y)与条件熵H(Y|X)之差称为互信息。决策树学习中的信息增益等价于训练数据集中类与特征的互信息。
3.模型建立
具体的决策树算法流程,我们在这里就不仔细介绍了,详细算法可以参阅李航老师的《统计学习方法》一书。
1 import numpy as np 2 import matplotlib.pyplot as plt 3 import matplotlib as mpl 4 from sklearn.tree import DecisionTreeClassifier 5 6 7 def iris_type(s): 8 it = {b‘Iris-setosa‘: 0, b‘Iris-versicolor‘: 1, b‘Iris-virginica‘: 2} 9 return it[s] 10 11 iris_feature = u‘花萼长度‘, u‘花萼宽度‘, u‘花瓣长度‘, u‘花瓣宽度‘ 12 13 if __name__ == "__main__": 14 mpl.rcParams[‘font.sans-serif‘] = [u‘SimHei‘] 15 mpl.rcParams[‘axes.unicode_minus‘] = False 16 17 path = ‘../dataSet/iris.data‘ # 数据文件路径 18 data = np.loadtxt(path, dtype=float, delimiter=‘,‘, converters={4: iris_type}) 19 x_prime, y = np.split(data, (4,), axis=1) 20 21 feature_pairs = [[0, 1], [0, 2], [0, 3], [1, 2], [1, 3], [2, 3]] 22 plt.figure(figsize=(10, 9), facecolor=‘#FFFFFF‘) 23 for i, pair in enumerate(feature_pairs): 24 # 准备数据 25 x = x_prime[:, pair] 26 27 # 决策树学习 28 clf = DecisionTreeClassifier(criterion=‘entropy‘, min_samples_leaf=3) 29 dt_clf = clf.fit(x, y) 30 31 # 画图 32 N, M = 500, 500 33 x1_min, x1_max = x[:, 0].min(), x[:, 0].max() 34 x2_min, x2_max = x[:, 1].min(), x[:, 1].max() 35 t1 = np.linspace(x1_min, x1_max, N) 36 t2 = np.linspace(x2_min, x2_max, M) 37 x1, x2 = np.meshgrid(t1, t2) 38 x_test = np.stack((x1.flat, x2.flat), axis=1) 39 40 41 y_hat = dt_clf.predict(x) 42 y = y.reshape(-1) 43 c = np.count_nonzero(y_hat == y) # 统计预测正确的个数 44 print(‘特征: ‘, iris_feature[pair[0]], ‘ + ‘, iris_feature[pair[1]]) 45 print(‘\t预测正确数目:‘, c) 46 print(‘\t准确率: %.2f%%‘ % (100 * float(c) / float(len(y)))) 47 48 # 显示 49 cm_light = mpl.colors.ListedColormap([‘#A0FFA0‘, ‘#FFA0A0‘, ‘#A0A0FF‘]) 50 cm_dark = mpl.colors.ListedColormap([‘g‘, ‘r‘, ‘b‘]) 51 y_hat = dt_clf.predict(x_test) # 预测值 52 y_hat = y_hat.reshape(x1.shape) 53 plt.subplot(2, 3, i+1) 54 plt.pcolormesh(x1, x2, y_hat, cmap=cm_light) 55 plt.scatter(x[:, 0], x[:, 1], c=y, edgecolors=‘k‘, cmap=cm_dark) 56 plt.xlabel(iris_feature[pair[0]], fontsize=14) 57 plt.ylabel(iris_feature[pair[1]], fontsize=14) 58 plt.xlim(x1_min, x1_max) 59 plt.ylim(x2_min, x2_max) 60 plt.grid() 61 plt.suptitle(u‘决策树对鸢尾花数据的两特征组合的分类结果‘, fontsize=18) 62 plt.tight_layout(2) 63 plt.subplots_adjust(top=0.92) 64 plt.show()
在书面的代码中,为了可视化的方便,我们采用特征组合的方式,将鸢尾花的四个两两进行组合,分别建立决策树模型,并对其进行验证。
DecisionTreeClassifier(criterion=‘entropy‘, min_samples_leaf=3)函数为创建一个决策树模型,其函数的参数含义如下所示:
plt.suptitle(u‘决策树对鸢尾花数据的两特征组合的分类结果‘, fontsize=18)设置整个大画布的标题
plt.tight_layout(2) 调整图片的布局
plt.subplots_adjust(top=0.92) 自适应,绘图距顶部的距离为0.92
结果如下:
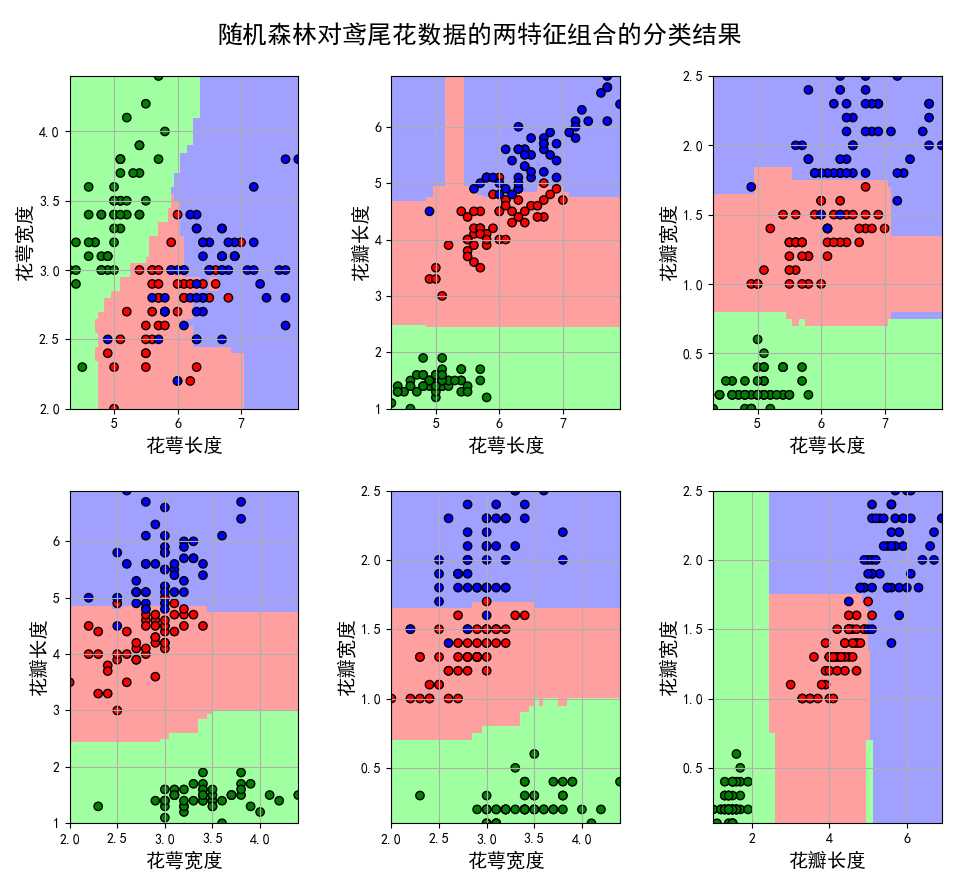
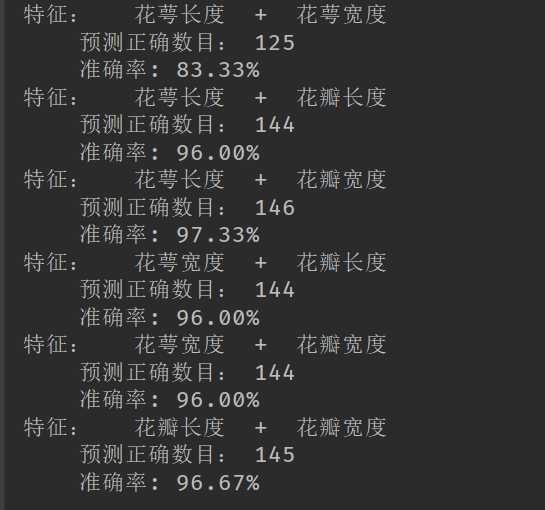
不同的特征组合的决策树模型的准确率:
4.决策树的保存
当我们通过建立好决策树之后,我们应该怎样查看建立好的决策树呢?sklearn已经帮助我们写好了方法,代码如下:
1 from sklearn import tree #需要导入的包 2 3 f = open(‘../dataSet/iris_tree.dot‘, ‘w‘) 4 tree.export_graphviz(model.get_params(‘DTC‘)[‘DTC‘], out_file=f)
当我们运行之后,程序会生成一个.dot的文件,我们能够通过word打开这个文件,你看到的是树节点的一些信息,我们通过graphviz工具能够查看树的结构:
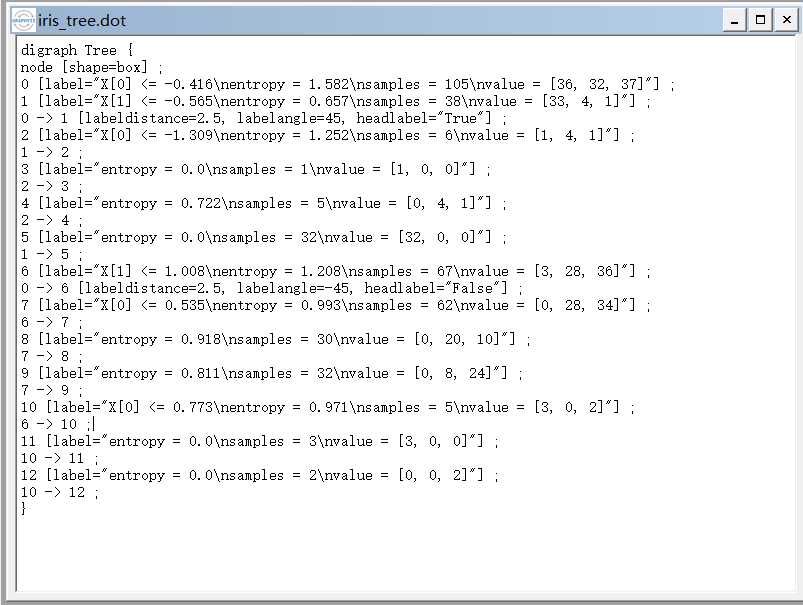
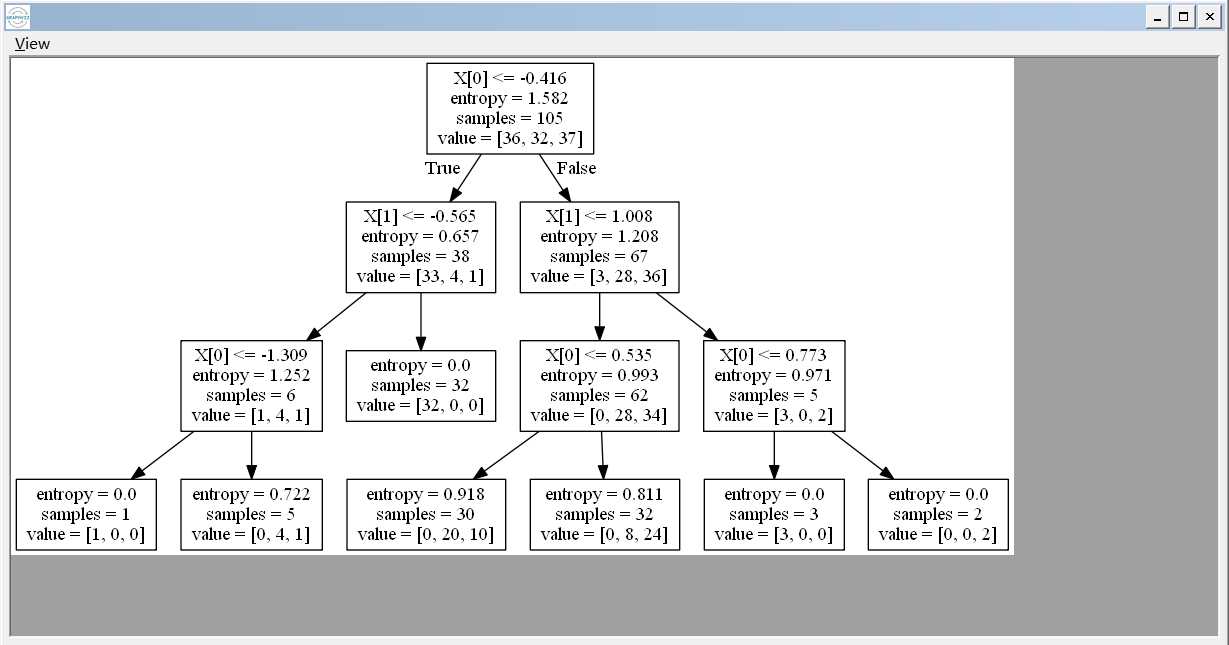
机器学习——决策树,DecisionTreeClassifier参数详解,决策树可视化查看树结构
标签:ane 怎样 dal lin 机器 count ade 预测 def
原文地址:https://www.cnblogs.com/baby-lily/p/10646226.html