标签:存储 name val lse == dep ret 命令 完全二叉树
先上题面
链接 https://pintia.cn/problem-sets/994805046380707840/problems/994805064676261888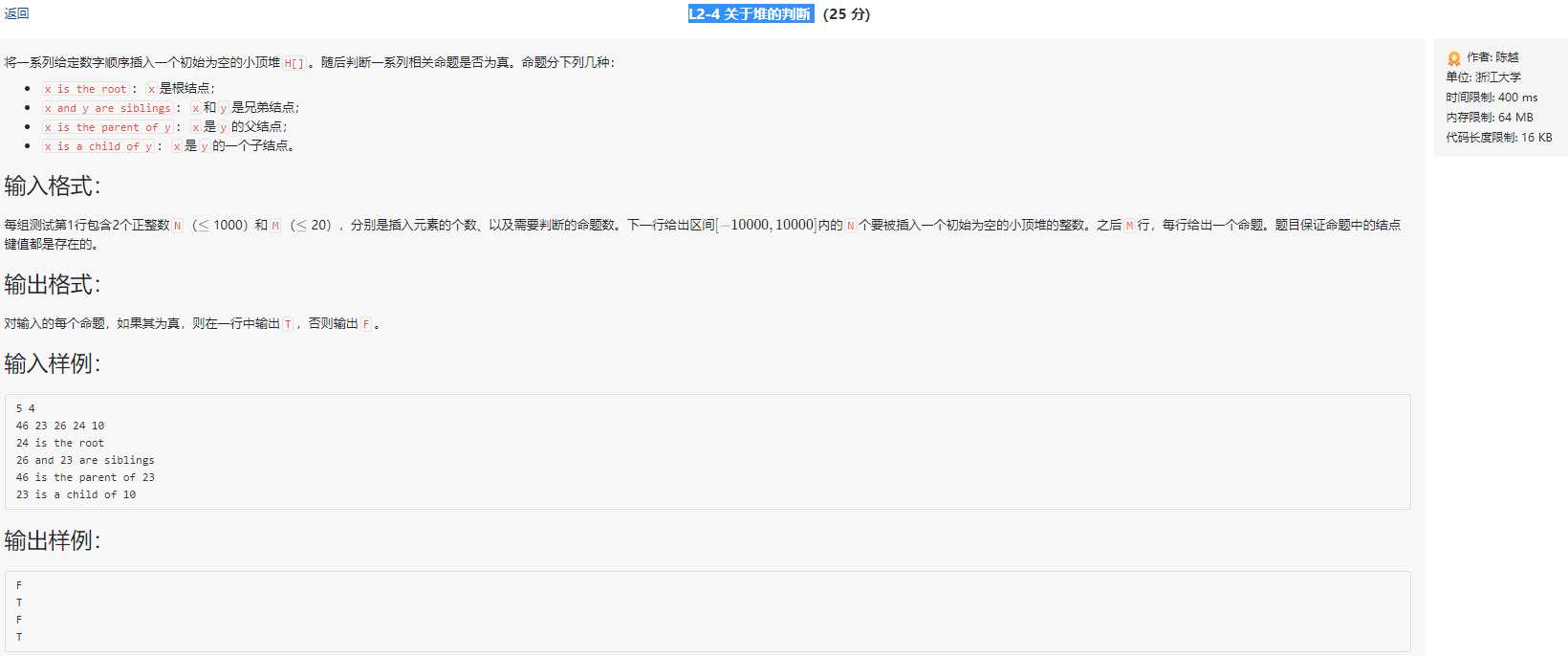
首先,题目描述的很清楚,这是一个关于最小堆的问题。题目的意思就是根据插入顺序建一个最小堆,然后对给出的命令进行判断,输出T or F。
因为堆其实就是一种特殊的二叉树,它具有两个性质: 1.结构性:用数组表示的完全二叉树。
2. 有序性:任一结点的关键字是其子树所有结点的最大值(最大堆)或最小值(最小堆)。
按照上述,我们应该很容易想到用数组存储这个堆,因为这样方便的进行元素的插入以及交换。
接下来就是进行建堆操作
其操作如下:
1.先将要插入的元素放在数组的末尾。
2.进行上浮交换操作,如果它小于它的父节点(在数组中表示为 i/2 ),则就进行交换。
3.不断插入元素,重复执行1,2操作。
完成建堆操作后,因为接下来进行的查询操作给出的是值,而我们则要根据下标来判断他们之间的关系。
所以要建立一个map映射关系,同时,因为查询中有父子结点的关系的判断,因此可以开个数组存储父子节点关系。
最后,就是执行查询操作了,输入的查询语句有一定规律,这个将在下面的代码中展示。
tips:因为输入的值存在负值,所以可以令num[0] = -1001,令num[1] - num[N]存值,这样才能保证建堆正确。
#include <cstdio> #include <vector> #include <map> #include <cstring> #include <algorithm> #include <iostream> using namespace std; int H[1005],fa[1005],depth[1005]; map<int,int>mp; void dui(int val,int site) { for(;val<H[site/2]&&site>0;site/=2) { swap(H[site],H[site/2]); } return ; } int main() { int n,m; scanf("%d %d",&n,&m); scanf("%d",&H[1]); H[0] = -10000000; for(int i = 2;i<=n;i++) { scanf("%d",&H[i]); dui(H[i],i); } for(int i = 1;i<=n;++i) mp[H[i]] = i; fa[1] = 0; for(int i = 2;i<=n;i++) { fa[i] = H[i/2]; } int a,b; string s; while(m--) { bool flag; scanf("%d",&a); cin >> s; if(s=="is") { cin >>s>>s; if(s=="root") { if(H[1]==a) flag = true; else flag = false; } else if(s=="child") { cin >> s; scanf("%d",&b); // printf("a==%d b==%d\n",a,b); if(fa[mp[a]]==b) flag = true; else flag = false; } else { cin >> s; scanf("%d",&b); if(fa[mp[b]]==a) flag = true; else flag = false; } } else { scanf("%d",&b); cin >>s >>s; if(fa[mp[a]]==fa[mp[b]]) flag = true; else flag = false; } if(flag) printf("T\n"); else printf("F\n"); } return 0; }
如果有所帮助,不胜荣幸。
标签:存储 name val lse == dep ret 命令 完全二叉树
原文地址:https://www.cnblogs.com/baihualiaoluan/p/10604198.html