标签：dai   a*   for   man   mamicode   target   post   arc   problems   

题意

233 Matrix

1 1
1
2 2
0 0
3 7
23 47 16

234
2799
72937

Hint

 

分析

参照whatbeg的题解。

题意：给出矩阵的第0行（233,2333,23333,...）和第0列a1,a2,...an（n<=10，m<=10^9），给出式子： A[i][j] = A[i-1][j] + A[i][j-1]，要求A[n][m]。

解法：看到n<=10和m<=10^9 应该对矩阵有些想法，现在我们假设要求A[a][b],则A[a][b] = A[a][b-1] + A[a-1][b] = A[a][b-1] + A[a-1][b-1] + A[a-2][b] = ...

这样相当于右图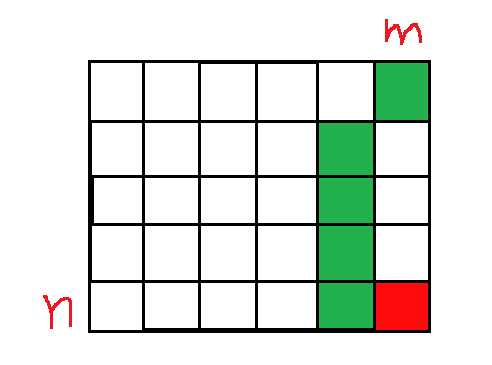：，红色部分为绿色部分之和，而顶上的绿色部分很好求，左边的绿色部分(最多10个)其实就是：A[1][m-1],A[2][m-1]..A[n][m-1],即对每个1<=i<=n, A[i][m]都可由A[1][m-1],A[2][m-1]..A[n][m-1]，于是建立12*12的矩阵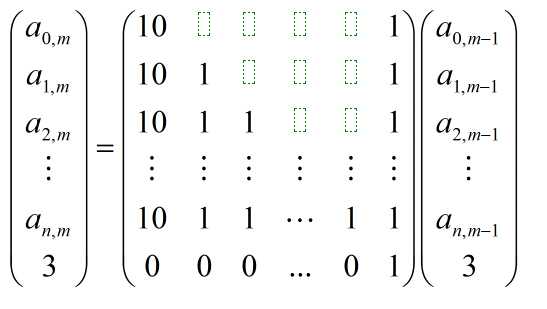：，将中间矩阵求m-1次幂，与右边[A[0][1],A[1][1]..A[n][1],3]^T相乘，结果就可以得出了。

时间复杂度\(O(n^3 \log m)\)

代码

#include<iostream>
#include<cstring>
#define rg register
#define il inline
#define co const
template<class T>il T read(){
    rg T data=0,w=1;rg char ch=getchar();
    while(!isdigit(ch)) {if(ch=='-') w=-1;ch=getchar();}
    while(isdigit(ch)) data=data*10+ch-'0',ch=getchar();
    return data*w;
}
template<class T>il T read(rg T&x) {return x=read<T>();}
typedef long long ll;
co int N=12,mod=10000007;
int n,m,t,A[N][N],ANS[N][N];
void mul(int a[N][N],int b[N][N]){
    static int c[N][N];
    for(int k=0;k<t;++k)
        for(int j=0;j<t;++j)if(b[k][j])
            for(int i=0;i<t;++i)if(a[i][k])
                (c[i][j]+=(ll)a[i][k]*b[k][j]%mod)%=mod;
    for(int i=0;i<t;++i)for(int j=0;j<t;++j)
        b[i][j]=c[i][j],c[i][j]=0;
}
int main(){
//  freopen(".in","r",stdin),freopen(".out","w",stdout);
    while(~scanf("%d%d",&n,&m)){
        memset(ANS,0,sizeof ANS),memset(A,0,sizeof A);
        ANS[0][0]=23,ANS[n+1][0]=3;
        for(int i=1;i<=n;++i) ANS[i][0]=read<int>()%mod;
        for(int i=0;i<=n;++i) A[i][0]=10,A[i][n+1]=1;
        for(int i=1;i<=n;++i)for(int j=i;j<=n;++j) A[j][i]=1;
        A[n+1][n+1]=1;
        for(t=n+2;m;m>>=1,mul(A,A))
            if(m&1) mul(A,ANS);
        printf("%d\n",ANS[n][0]);
    }
    return 0;
}

HDU5015 233 Matrix

标签：dai   a*   for   man   mamicode   target   post   arc   problems   

原文地址：https://www.cnblogs.com/autoint/p/10659276.html