标签:数组 problem 限制 情况 状态 img OLE fit 初始化
题源:https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-iv/
本题代码:
1 /** 2 * @author yuan 3 * @version 0.1 4 * @date 2019/4/5 5 */ 6 public class Leetcode188 { 7 8 private int getBetterBuy(int[] buy, int[] sell, int price, int i) { 9 if (i == 0) { 10 return Math.max(buy[i],-price); 11 } else { 12 return Math.max(buy[i], sell[i - 1] - price); 13 } 14 } 15 16 private int getBetterSell(int[] buy, int[] sell, int price, int i) { 17 return Math.max(sell[i], buy[i] + price); 18 } 19 20 /** @see Leetcode122 */ 21 public int greedy(int[] prices) { 22 int result = 0; 23 // 当前是否持有股票 24 boolean has = false; 25 // 当前所持有股票的购入价 26 int buyInPrice = 0; 27 for (int i = 0; i < prices.length; i++) { 28 if (!has) { 29 if (i + 1 < prices.length && prices[i + 1] > prices[i]) { 30 has = true; 31 buyInPrice = prices[i]; 32 } 33 } else if (i + 1 == prices.length || prices[i + 1] < prices[i]) { 34 has = false; 35 result += prices[i] - buyInPrice; 36 } 37 } 38 return result; 39 } 40 41 /** @see Leetcode123 */ 42 public int maxProfit(int k, int[] prices) { 43 if (k <= 0 || prices == null || prices.length == 0) { 44 return 0; 45 } 46 // k足够大的时候退化为贪心 47 if (k >= prices.length / 2) { 48 return greedy(prices); 49 } 50 // 第i次买的收益 51 int[] buy = new int[k]; 52 for (int i = 0; i < k; i++) { 53 buy[i] = Integer.MIN_VALUE; 54 } 55 // 第i次卖的收益 56 int[] sell = new int[k]; 57 for (int price : prices) { 58 for (int j = 0; j < k; j++) { 59 buy[j] = getBetterBuy(buy, sell, price, j); 60 sell[j] = getBetterSell(buy, sell, price, j); 61 } 62 } 63 return sell[k - 1]; 64 } 65 }
整体思路:
要进行n次交易,至少需要2n天,如果k大于或等于数组长度的一半,那么这题就退化为买卖股票的最佳时机 II,采用贪心法来做(见Leetcode上的题解)。
如果k小于数组长度的一半,那么就变成了买卖股票的最佳时机 III的扩展,买卖股票的最佳时机 III动态规划解法如下:
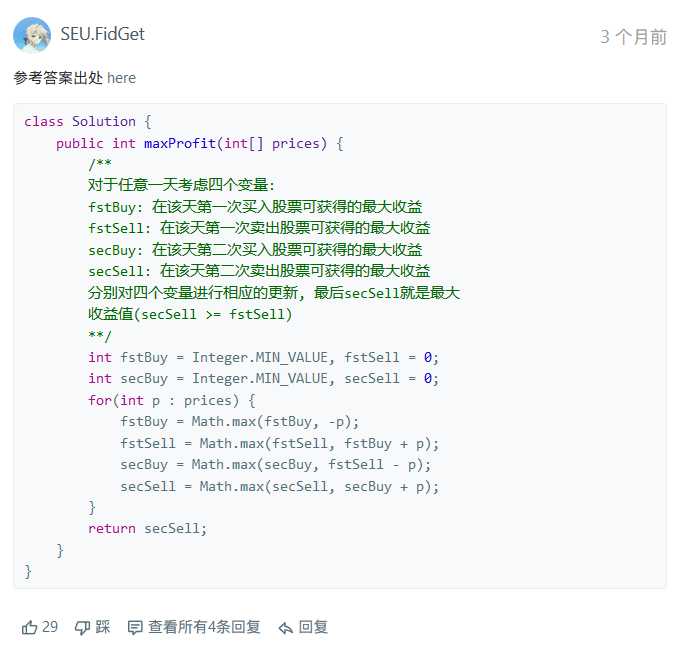
原出处:https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iii/discuss/39611/Is-it-Best-Solution-with-O(n)-O(1).
将这4个变量扩展为2k个变量,用数组保存,以同样方式处理,之后返回最后一次出售的收益即可。
本题动态规划的具体细节与买卖股票的最佳时机 III相同。
本题状态转移方程:
but[t][i] = max{ buy[t-1][i], sell[t-1][i-1] - prices[t] }
sell[t][i] = max{ sell[t-1][i], buy[t-1][i] + prices[t] }
其中t表示天数,i表示交易次数。具体说明见下文。
t这个维度可以用滚动数组省去。
算法细节:
将买卖股票的最佳时机 III的动态规划结合买卖股票的最佳时机 II的贪心写出这题的代码不难,如果你已经明白买卖股票的最佳时机 III的动态规划算法是怎么回事,那么下面的这一堆字就没必要看了??。下面是对上文本题代码的解释。
首先要明确buy[i]和sell[i]含义。用t表示考虑前t天的情况(从0开始),并将在最晚第t天进行至多第i次购入的收益表示为buy[t][i],在最晚第t天进行至多第i次出售的收益表示为sell[t][i]。显然购入操作的将带来负收益。题目给的k是指最多进行k次交易,而最优解的交易次数可能是小于k的,因此buy[t][i]和sell[t][i]的含义并不是第i次购入或出售后的收益,而是指在该天进行第[小于或等于i]次购入或出售后的收益。比如k=2,prices={2,4,1,0,0,0,0,0}的情况,显然第1天购入第2天出售可以获得最大收益,最终结果sell[t=7][i=1]应与sell[t=1][i=0]的值相同。也就是说,如果最优解一共进行了x次交易,且这次交易的出售在第y天进行,那么对所有i>=x,t>=y,buy[t][i]与sell[t][i]必须分别等于buy[y][x]和sell[y][x],最终结果才能用sell[prices.length-1][k-1]表示。采用滚动数组可以省去天数这个维度,但下文部分地方为方便说明,仍会把天数标出。
明确buy[]和sell[]的含义后,状态转移方程本身是否正确比较好理解,这里不进行解释。
第i次出售必须在第i次购入之后进行,并且每天只能进行一次操作,那么每天都计算整个buy[]和sell[]数组不会出错吗?并不会。
假设一天可以进行多次操作,如果同一天各一次买入和卖出,这两次操作是不会有收益的,所以在第一天计算第一次出售的收益会是0。既然在第一天进行第一次出售的收益是0,那么第一天进行第二次购入的收益就将和第一次购入的收益相同,如果闲得蛋疼,买一次卖一次再买一次再卖一次,最后再买第三次,产生的收益也和第一次购入相同。如果第一天进行了第一次购入,第二天进行第一次售出后再进行第二次购入,那么就相当于这一天什么也没做,总收益仍然等于第一天的第一次购入产生的收益。依此类推不难发现,如果在每天只能操作依次时当前这一天至多只能进行第x次购入,那么取消限制后,对于所有i>x,buy[i]是等于buy[x]的,并且sell[x]等于sell[x-1],接着可以推出所有这些sell[i]都等于sell[x-1]。因此,对于每个prices[i],即每一天,都对整个buy[]和sell[]数组进行计算,可以使得sell[k-1]等于最优解的收益。于是sell[k-1]就是我们要的结果。
以k=2,prices={2,4,1,1,0}为例说明:
首先初始化buy[]为全-∞(Java中用Integer.MIN_VALUE模拟),sell[]为全0。
在第1天(t=0),buy[0]显然会等于-price[0],即-2。
此时虽然还不能产生第1次出售,但sell[0]=max{sell[0],buy[0]+prices[0]},结果将会是0。
此时虽然还不能产生第2次购入,但buy[1]=max{buy[1],sell[0]-prices[0]},将和buy[0]相等。
此时虽然还不能产生第2次出售,但sell[1]=max{sell[1],buy[1]+prices[0]},结果也会是0。实际上既然buy[1]和buy[0]相等,sell[1]也就等于sell[0]。
于是,如果只考虑第1天,最大收益sell[1]是0,结果正确。
再考虑第2天(t=1)。
buy[0]=max{buy[0],sell[0]-prices[1]},结果仍然是-2。
sell[0]=max{sell[1],buy[0]+prices[1]},结果为2。
此时虽然还不能产生第2次购入,但由于buy[0][1]与buy[0][0]相等,且buy[1][1]=max{buy[0][1],sell[1][0]-prices[1]},相当于buy[1][1]=max{buy[0][0],sell[0][0]-prices[1]}。最终buy[1][1]和buy[1][0]相等,即第二天的buy[1]仍然和buy[0]相等,值为-2。
此时虽然还不能产生第2次出售,但sell[1]=max{sell[1],buy[1]+prices[1]},结果也是2。
在只考虑前2天的情况下,最大收益sell[1]是2,结果正确。
再考虑第3天。
buy[0]=max{buy[0],-prices[2]},变为-1。
sell[0]=max{sell[0],buy[0]+prices[2]},仍为2。
buy[1=max{buy[1],sell[0]-prices[2]},变为1。
此时虽然还不能产生第2次出售,sell[1]=max{sell[1],buy[1]+prices[2]},结果仍为2。
于是只考虑前3天的情况下,最大收益sell[1]为2,结果正确。
再考虑第4天。
buy[0]=max{buy[0],-prices[3]},仍为-1。
sell[0]=max{sell[0],buy[0]+prices[3]},仍为2。
buy[1]=max{buy[1],sell[0]+prices[3]},仍为1。
sell[1]=max{sell[1],buy[1]+prices[3]},仍为2。
于是只考虑前4天的情况下,最大收益sell[1]为2,结果正确。
最后考虑第5天
buy[0]=max{buy[0],-prices[4]},变为0。
sell[0]=max{sell[0],buy[0]+prices[4]},仍为2。
buy[1]=max{buy[1],sell[0]+prices[4]},变为2。
sell[1]=max{sell[1],buy[1]+prices[4]},仍为2。
最终最大收益sell[1]为2,结果正确。
附另外两题的代码
1 /** 2 * @author yuan 3 * @version 0.1 4 * @date 2019/4/5 5 */ 6 public class Leetcode122 { 7 public int maxProfit(int[] prices) { 8 int result = 0; 9 int buyInPrice = 0; 10 boolean has = false; 11 for (int i = 0; i < prices.length; i++) { 12 if (!has) { 13 if (i + 1 < prices.length && prices[i + 1] > prices[i]) { 14 has = true; 15 buyInPrice = prices[i]; 16 } 17 } else if (i + 1 == prices.length || prices[i + 1] < prices[i]) { 18 has = false; 19 result += prices[i] - buyInPrice; 20 } 21 } 22 return result; 23 } 24 }
1 /** 2 * @author yuan 3 * @version 0.1 4 * @date 2019/4/5 5 */ 6 public class Leetcode123 { 7 public int maxProfit(int[] prices) { 8 /* 9 对于任意一天考虑四个变量: 10 firstBuy: 在该天第一次买入股票可获得的最大收益 11 firstSell: 在该天第一次卖出股票可获得的最大收益 12 secondBuy: 在该天第二次买入股票可获得的最大收益 13 secondSell: 在该天第二次卖出股票可获得的最大收益 14 分别对四个变量进行相应的更新, 最后secSell就是最大 15 收益值(secondSell >= firstBuy) 16 */ 17 int firstBuy = Integer.MIN_VALUE; 18 int firstSell = 0; 19 int secondBuy = Integer.MIN_VALUE; 20 int secondSell = 0; 21 for (int price : prices) { 22 firstBuy = Math.max(firstBuy, -price); 23 // 如果在第一天,这个结果是0 24 firstSell = Math.max(firstSell, firstBuy + price); 25 // 如果在第一天,将等于firstBuy;如果在第二天,由于第一天等于firstBuy,仍将等于firstBuy 26 secondBuy = Math.max(secondBuy, firstSell - price); 27 // 如果在前两天,由于secondBuy等于firstBuy,结果等于firstSell;如果在第三天,secondBuy + price等于firstSell 28 secondSell = Math.max(secondSell, secondBuy + price); 29 } 30 return secondSell; 31 } 32 }
[Leetcode188] 买卖股票的最佳时机IV 动态规划 解题报告
标签:数组 problem 限制 情况 状态 img OLE fit 初始化
原文地址:https://www.cnblogs.com/null-0/p/10659432.html