标签:neo4j 区间 停止 之间 3.3 均值 4.6 有序 log
3.1 数据预处理
数据质量的三个要素:准确性、完整性和一致性。
3.1.2 数据预处理的主要任务
数据清理:填写缺失的值,光滑噪声数据,识别或删除离群点,并解决不一致性来”清理“数据。
数据集成:相关性分析,卡方,协方差,相关系数
数据归约:大->小,维归约,数据压小
数据变换和数据离散化:规范化,离散化
3.2 数据清理
3.2.1 缺失值
1.忽略元组
2.人工填写缺失值
3.使用一个全局常量填充缺失值
4.使用属性的中心度量填充缺失值:中位数
5.使用与给定元组属同一类的所有样本的属性均值或中位数
6.使用最可能的值填充缺失值:回归/贝叶斯/决策树
第6种是最流行的策略
3.2.2 噪声数据
噪声:被测量的变量的随机误差或方差。
数据光滑技术:
分箱:通过考察数据的近邻来光滑有序数据值。这些有序的值被分布到一些桶或箱中。由于分箱考察近邻的值,因此它进行局部光滑。
例:4,8,15,21,21,24,25,28,34
分箱:每箱3个值
箱1:4,8,15
箱2:21,21,24
箱3:25,28,34
用均值光滑:
箱1:9,9,9
箱2:22,22,22
箱3:29,29,29
用箱边界光滑:宽度越大,光滑效果越明显
箱1:4,4,15
箱2:21,21,22
箱3:25,25,34
回归:用一个函数拟合数据来光滑数据。线性回归涉及找到拟合两个属性的最佳直线,使得一个属性可以用来预测另一个。
离群点分析:通过聚类来检测离群点。
3.3 数据集成
3.3.1 实体识别问题
3.3.2 冗余和相关分析
有些冗余可以被相关分析检测到。给定两个属性,这种分析可以根据可用的数据,度量一个属性能在多大程度上蕴含另一个。
对于标称数据,用卡方检验,对于数值属性,用相关系数和协方差,它们都评估一个属性的值如何随另一个变化。
1.标称数据的卡方相关检验
卡方统计检验假设A和B是独立的。
例3.1 使用卡方的标称属性的相关分析
假设调查了1500个人,记录性别,是否小说,那么有两个属性:性别、是否小说。
| 男 | 女 | 合计 | |
| 小说 | 250(90) | 200(360) | 450 |
| 非小说 | 50(210) | 1000(840) | 1050 |
| 合计 | 300 | 120 | 1500 |
单元(男,小说)的期望频率是:
e11=count(男)*count(小说)/n=300*450/1500=90
根据卡方值公式:

自由度是(2-1)(2-1)=1
2.数值数据的相关系数
对于数值数据,可以通过计算A和B的相关系数,估计这两个属性的相关度rA,B

该值处于-1到1之间,如果rA,B大于0,则正相关,意味着A值随着B值增大而增大。该值越大,相关性越强。因此一个较高的rA,B表明A或B可以作为冗余而被删除。
如果该值为0,说明是独立的,没有相关性。
如果该小于0,说明是负相关,一个值增加另一个减少。
注意,相关性并不蕴涵因果关系,如果A和B是相关的,并不意味着A导致B或B导致A。
3.数值数据的协方差
协方差和方差是两个类似的度量,评估两个属性如何一起变化。A和B的均值又称为期望值。
A和B的协方差定义为:
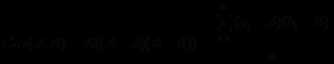

对于两个趋向于一起改变的属性A和B,如果A大于E(A),B很可能大于E(B)。因此,A和B的协方差为正。另一方面,如果一个属性小于它的期望值,另一个属性趋势向于大于它的期望值,则A和B的协方差为负。
如果A和B是独立 的,E(AB)=E(A)*E(B),则协方差为0。但是如果协方差为0,未必是独立的。、
例:数值属性的协方差分析
| 时间点 | AllElectronics | HighTech |
| t1 | 6 | 20 |
| t2 | 5 | 10 |
| t3 | 4 | 14 |
| t4 | 3 | 5 |
| t5 | 2 | 5 |
E(AllElectronics)=(6+5+4+3+2)/5=4
E(HighTech)=(20+10+14+5+5)/5=10.8
Cov=(6*20+5*10+4*14+3*5+2*5)/5-4*10.8=50.2-43.2=7
协方差为正,说明两个公司股票同时上涨
3.3.3 元组重复
3.3.4 数据值冲突的检测与处理
3.4 数据归约
3.4.1 数据归约策略
维归约:减少所考虑的随机变量或属性的个数。方法包括小波变换和主成分分析,它们把原数据变换或投影到较小的空间。属性子集选择是一种维归约方法,其中不相关、弱相关或冗余的属性或维被检测和删除。
数量归约:用替代的、较小的数据表示形式替换原数据。这些技术可以是参数的或非参数的。对于参数方法而言,使用模型估计数据,使得一般只需要存放模型参数,而不是实际数据。如回归和对数-线性模型。存放数据归约表示的非参数方法包括直方图、聚类、抽样和数据立方体聚集。
数据压缩:
3.4.2 小波变换
3.4.3 PCA:搜索k个最能代表数据的n维正交向量,其中k<=n。
PCA常常能够提示先前未曾察觉的联系,并因此允许解释不寻常的结果。
基本过程如下:
(1)对输入数据规范化,使得每个属性都落入相同的区间。
(2)PCA计算k个标准正交向量,作为规范化输入数据的基。这些是单位向量,每个都垂直于其他向量。这些向量称为主成分。输入数据是主成分的线性组合。
(3)对主成分按“重要性”或强度降序排列。这一信息帮助识别数据中的组群或模式。
(4)既然按“重要性”降序排列,因此可以通过去掉较弱的成分来归约数据。
PCA可以用于有序和无序的属性、并且可以处理稀疏和倾斜数据。
3.4.4 属性子集选择
属性子集选择通过删除不相关或冗余的属性减少数据量。属性子集选择的目标是找出最小属性集,使得数据类的概率分布尽可能地接近使用所有属性得到的原分布。
最好的和最差的属性通常使用统计显著性检验来确定。这种检验假定属性是相互独立的。也可以使用一些其他属性评估度量,如建立分类决策树使用的信息增益度量。
(1)逐步向前选择:由空属性集作为归约集开始,确定原属性集中最好的属性,并将它添加到归约集中。在其后的每一次迭代,将剩下的原属性集中的最好的属性添加到该集合中。
(2)逐步向后删除:该过程由整个属性集开始。在每一步中,删除尚在属性集中最差的属性。
(3)逐步向前选择和逐步向后删除的组合:每一步选择一个最好的属性,并在剩余属性中删除一个最差的属性。
(4)决策树归纳:决策树算法最早是用于分类的。决策树归纳构造一个类似于流程图的结构,其中每个内部结点表示一个属性上的测试,每个分枝对应于测试的一个结果;每个外部结点表示一个类预测。在每个结点上,算法选择最好的属性,将数据划分成类。
当决策树归纳用于属性子集选择时,由给定的数据构造决策树。不出现在树中的所有属性假定是不相关的,出现在树中的属性形成归约后的属性子集。这些方法的结束条件可以不同。该过程可以使用一个度量阈值来决定何时停止属性选择过程。
可以创建一些新属性来帮助提高准确性和对高维数据结构的理解。比如通过高度和宽度构造属性面积。
3.4.5 回归和对数线性模型:参数化数据归约
回归和对数线性模型可以用来近似给定的数据。
在线性回归中,对数据建模型,使之拟合到一条直线。
例:y=wx+b,w和b分别为直线的斜率和截距。系数可以用最小二乘法求解,
多元回归是线性回归的扩展,允许用两个或多个自变量的线性函数对因变量y建模。
对数线性模型近似离散的多维概率分布。
3.4.6 直方图
等宽直方图:每个桶的宽度区间是一致的。
等频直方图:使得每个桶的频率粗略地为常数。
3.4.7 聚类
3.4.8 抽样
无放回简单随机抽样
有放回简单随机抽样
簇抽样
分层抽样
3.4.9 数据立方体聚集
3.5 数据变换与数据离散化
3.5.1 数据变换策略
(1)光滑:去掉数据中的噪声。包括分箱、回归和聚类
(2)属性构造:可以由给定的属性构造新的属性并添加到属性集中
(3)聚集:汇总或聚集
(4)规范化:把属性数据按比例缩放
(5)离散化:数值属性的原始值用区间标签或概念标签替换。
(6)由标称数据产生概念分层:
离散化技术划分:监督和非监督
离散化技术划分:自顶向下或自底向上
自顶向下:先找出一个或几个点来划分整个属性区间,在结果区间上递归重复这一过程。
自底向上:将所有的连续值看做可能的分裂点,通过合并领域的值形成区间,在区间递归地应用这一过程。
3.5.2 通过规范化变换数据
最小-最大规范化:保持原始数据之间的联系,如果后续的实例落在当日数据值域之外,将面临 越界错误
z分数规范化:当最小值和最大值未知,或离群点左右了最小-最大规范化时,该方法是有用的。
小数定标规范化:通过移动属性A的值的小数点位置进行规范化。
有必要保留规范化参数,以便将来的数据可以用一致的方式规范化。
3.5.3 通过分箱离散化
3.5.4 通过直方图分析离散化
3.5.5 通过聚类、决策树和相关分析离散化
3.5.6 标称数据的概念分层产生
关系其它精华NEO4JLEE:
清洗什么:https://blog.csdn.net/weixin_40683253/article/details/82221029
离散化:https://www.cnblogs.com/jiaxin359/p/8574510.html
标签:neo4j 区间 停止 之间 3.3 均值 4.6 有序 log
原文地址:https://www.cnblogs.com/muffe/p/10663189.html