标签:font inf ace 有关 二分 因此 初始化 ima bsp
原题:https://codeforces.com/contest/1119/problem/D
题意大概是一个n行1e18列的矩阵,其中每行第一个数为s[i],剩下的数每行依次以1的速度递增。就是说,矩阵元素 a[i][j] = s[i] + j 。有q个询问,每个询问有两个参数l,r,求矩阵第l列到第r列(所有行)一共出现了几个不同的数。
这道题首先要先想到,两个参数 [l,r] 其实等价于一个参数 [0,r-l] ,也就是说矩阵第0~r-l行出现的数字的个数其实和第l-r行出现的个数是一样的。我们可以这样理解:[l,r] 和 [0,r-l] 代表的区域本质上是两个矩形,而他们的位置关系就是平移而已,如下图两个矩阵,他们的大小一致,因此其中元素有一一对应的关系,也就是每个数都减去(向左平移)了 l 个单位。而整体的数字出现的个数是不变的。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ... | |
| 0 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ... |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... |
| 2 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ... |
| 3 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ... |
| 5 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | ... |
<--向左平移L个单位<--
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ... | |
| 0 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ... |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... |
| 2 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ... |
| 3 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ... |
| 5 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | ... |
现在,我们可以把每一行看作一个 [s[i],s[i]+r-l] 的闭区间,于是我们把这n个闭区间放到数轴上,如果没有重合,那么答案就是n*(r-l+1)了,但显然区间重合是可能存在的。最暴力的想法就是初始化一个mark[值域]数组,对每一个区间里的数字逐个mark上,最后再遍历值域。然而这玩意儿一次询问就是O(n*值域),显然不行。
这时我们观察数轴上的这n个闭区间,发现他们无论何时(每组询问)的长度都是一致的,因此我们可以把这些区间分成两类:如果对于一个区间I = [xi,yi], 存在区间J = [xj,yj], 使得xj <= yi,我们说区间I是”贡献确定“的,因为由于区间长度一致,区间I在yi之后的数字都可以由区间J所替代,所以此时区间I的贡献确定为yi-xi。相反地,如果不存在这样的区间J,那么区间I就是”贡献不确定“的,他的贡献与区间长度有关(其实就是长度+1,闭区间嘛)。
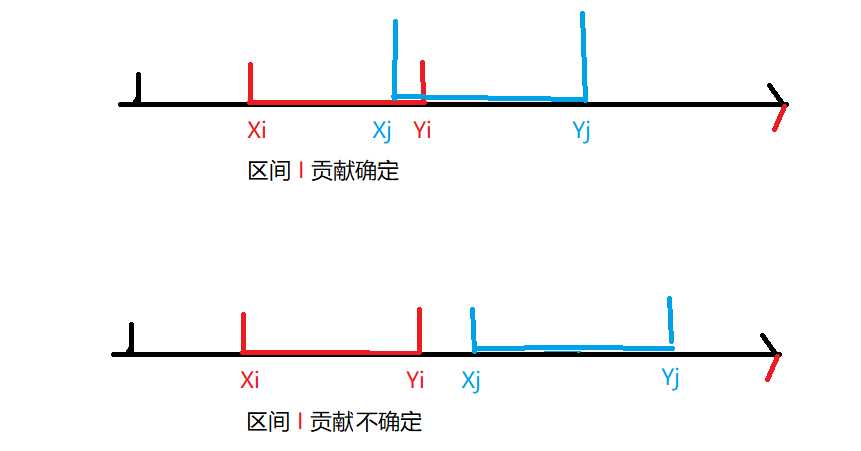 (劣质示意图)
(劣质示意图)
回到这道题,每个询问等价的那个参数(记作q[k], q[k] = rk-lk),本质上就是那个区间长度,所以我们知道对于每个”贡献不确定“的区间,他的贡献是q[k] + 1。那对于”贡献确定“的区间。。。废话他们的贡献都确定了好吗。那这个确定的贡献是多少呢,我们可以把这n个区间排个序,排好序之后第i个区间的确定贡献(也就是最大的贡献,记作t[i])就是 t[i] = s[i+1] - s[i] , 也就是他和下一个区间开头的距离了。最后,判断一个区间是否确定贡献的方式就是判断t[i] 与 q[k] 的大小关系,如果t[i] <= q[k], 那么他的区间尾就碰到了下一个区间头,贡献就确定为t[i]了。我们可以将 t[i] 排序,二分查找有多少个区间为确定贡献的。
那么,对于每一个询问 q[k], 覆盖的数字的个数 ans[k] = Σpi=1t[i] + (n-p) * (rk-lk+1), 其中p代表有且仅有前p小的t[i] 小于q[k]。需要前缀和数组sum[p]记录前p个t[i] 的和。
代码如下:
1 #include<iostream> 2 #include<algorithm> 3 #include<cstdio> 4 using namespace std; 5 typedef unsigned long long ull; 6 const int maxN = 1e5 + 3; 7 const ull inf = 3e18; 8 ull n, s[maxN] = {0}, qn, q[maxN] = {0}, t[maxN] = {0}, sum[maxN] = {0}; 9 int main() 10 { 11 ull temp; 12 ios::sync_with_stdio(false); 13 cin >> n; 14 for(int i = 1; i <= n; i++) 15 cin >> s[i]; 16 cin >> qn; 17 for(int i = 1; i <= qn; i++) 18 { 19 cin >> temp >> q[i]; 20 q[i] -= temp; 21 } //读入,询问参数二变一 22 23 sort(s+1,s+1+n); 24 t[0] = 0; 25 for(int i = 1; i < n; i++) 26 t[i] = s[i+1] - s[i]; 27 t[n] = inf; // 最后一个区间永远也不会与下一个区间重合,贡献是不确定的 28 sort(t,t+n); // sort记得写在前缀和之前。。。 29 for(int i = 1; i < n; i++) 30 sum[i] = sum[i-1] + t[i]; 31 32 for(int i = 1; i <= qn; i++) 33 { 34 int l = 0, r = n-1, mid; // q可能小于所有的t,但不可能大于所有的t 35 while(l < r) 36 { 37 mid = (l+r+1) >> 1; // 记得+1,防止死循环 38 if(t[mid] <= q[i]) 39 l = mid; 40 else 41 r = mid - 1; 42 } 43 cout << sum[l] + (q[i]+1) * (n-l) << ‘ ‘; 44 } 45 cout << endl; 46 47 return 0; 48 }
Frets On Fire --- 2019 Codeforces Global Round 2 Problem D
标签:font inf ace 有关 二分 因此 初始化 ima bsp
原文地址:https://www.cnblogs.com/Colossus/p/10665205.html