标签:tac [] 就会 (()) size ring http dex output
Given a string containing just the characters ‘(‘ and ‘)‘, find the length of the longest valid (well-formed) parentheses substring.
Example 1: Input: "(()" Output: 2 Explanation: The longest valid parentheses substring is "()"
Example 2: Input: ")()())" Output: 4 Explanation: The longest valid parentheses substring is "()()"
思路
这道题一开始我想到的是使用辅助空间栈来解决这个问题,我们在栈中存储下标,然后将匹配的括弧弹出,然后使用当前下标减去栈中最上面元素的下标得到长度,如果栈为空的话,我们移动index表示到当前下标。直到遍历完毕。时间复杂度位O(n),空间复杂度为O(n)
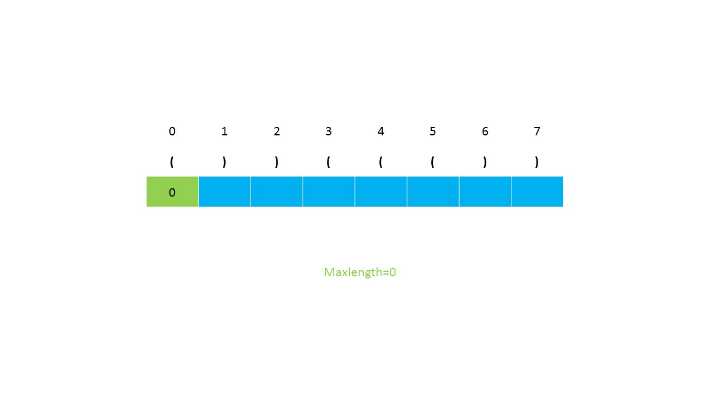
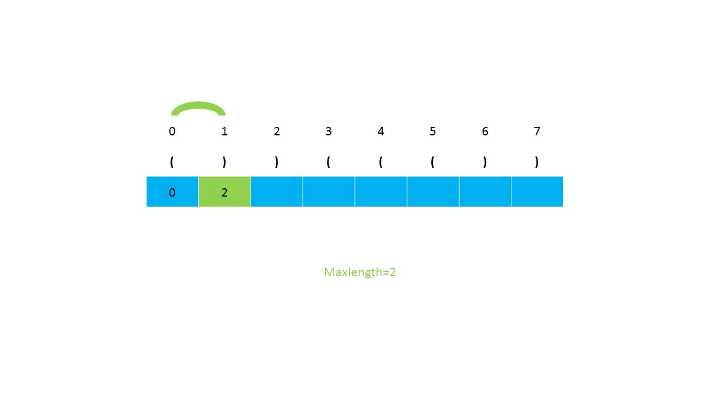
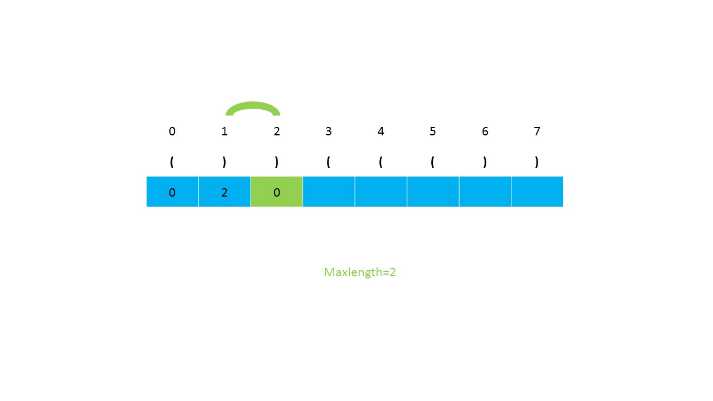
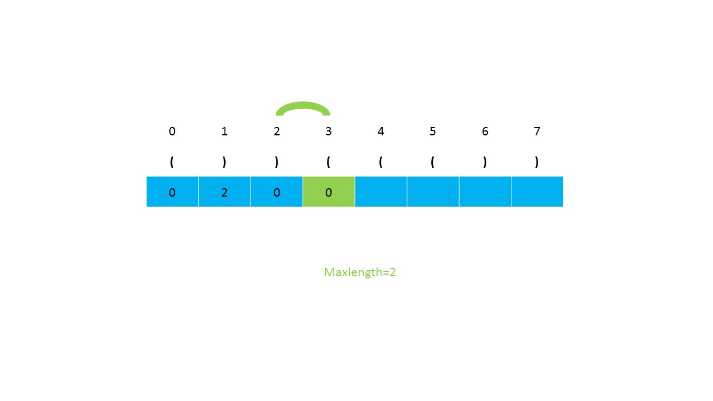
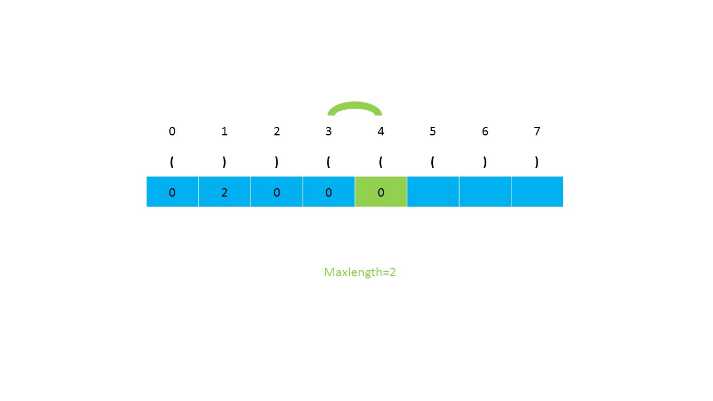
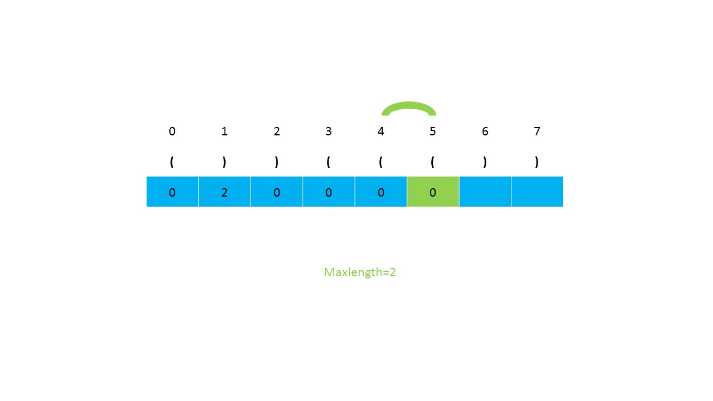
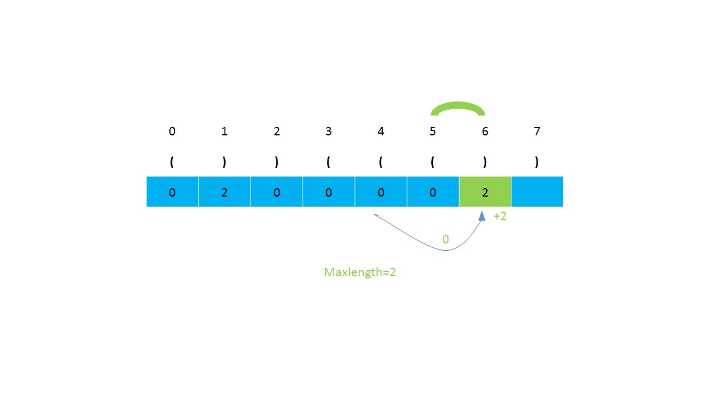
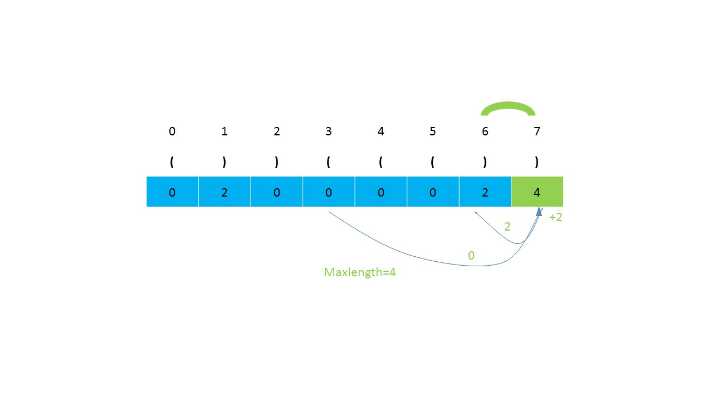
第二种思路是使用动态规划,我们设置一个辅助数组,然后对应元素的下标存储当前的有效长度,一直遍历到最后,返回数组中最长的长度。当遍历到i位置为‘)‘时,我们判断i-1的位置是否是‘(‘,接下来判断i-2是否大于等于0(因为小标为2的前面不会存在可以匹配的字符)。如果i-1的位置不为‘(‘,就会存在‘(())‘这种情况,所以需要需要对前面的s[i-dp[i-1]-1] 位检查是否是 ‘(‘。之后继续判断下标大小是否满足。时间复杂度为O(n),空间复杂度为O(n)。
第一种思路图示
第二种思路的图示
第一种实现代码
1 class Solution:
2 def longestValidParentheses(self, s):
3 """
4 :type s: str
5 :rtype: int
6 """
7 max_len, index = 0, -1
8 stack = []
9 for i , char in enumerate(s):
10 if char == ‘(‘:
11 stack.append(i)
12 else:
13 if stack:
14 tem = stack.pop()
15 if stack:
16 max_len = max(max_len, i - stack[-1])
17 else:
18 max_len = max(max_len, i - index)
19 else:
20 index = i
21 return max_len
第二种思路实现代码
1 class Solution(object):
2 def longestValidParentheses(self, s):
3 """
4 :type s: str
5 :rtype: int
6 """
7 if len(s) < 2:
8 return 0
9 dp = [0]* len(s)
10 for i in range(1, len(s)):
11 if s[i] == ‘)‘:
12 if s[i-1] ==‘(‘:
13 if i - 2 >=0:
14 dp[i] = dp[i-2] + 2
15 else:
16 dp[i]= 2
17 elif (i -dp[i-1]) > 0 and s[i-dp[i-1]-1] == ‘(‘:
18 if i -dp[i-1] -2 >= 0:
19 dp[i] = dp[i-1] + 2 + dp[i-dp[i-1]-2]
20 else:
21 dp[i] = 2+ dp[i-1]
22 return max(dp)
【LeetCode每天一题】Longest Valid Parentheses(最长有效括弧)
标签:tac [] 就会 (()) size ring http dex output
原文地址:https://www.cnblogs.com/GoodRnne/p/10676111.html