标签:+= http names std 技术 一个 using code ems

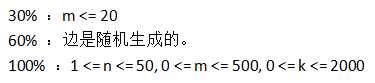
没注意 “第 x 条边和第 y 条边的起点是相同的” 的限制。没想出来。
有这个限制,可以考虑每个点分别计算。令 \( f[i] \) 表示从 i 出发的最大边数期望,那么先把拓扑序在自己之后的点的 \( f[ ] \) 算出来,然后考虑自己这个点的出边怎么做能使自己的 \( f[ ] \) 最大。
\( f[i]=\frac{ \sum f[j]+1 }{ d } \) ,其中 d 是保留下来的边数, j 是保留边指向的点。
如果把 \( f[ ]+1 \) 看做收益, 1 看做代价,那么这个式子就是 0/1 分数规划。考虑二分找出最优比率。
已有二分值,每条出边的权值就确定了。考虑选一个权值和最大的出边集合。限制条件意为选了 x 必须选 y ,所以这是一个最大权闭合子图的问题。用最小割求解即可。(不用把成环的限制缩点!)
注意每次网络流之后要把 hd 和 cap 都赋回原值。
#include<cstdio> #include<cstring> #include<algorithm> #include<vector> #define db double #define pb push_back using namespace std; int rdn() { int ret=0;bool fx=1;char ch=getchar(); while(ch>‘9‘||ch<‘0‘){if(ch==‘-‘)fx=0;ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘)ret=ret*10+ch-‘0‘,ch=getchar(); return fx?ret:-ret; } const int N=55,M=505,K=2005; int n,m,k,hd[N],xnt,to[M],nxt[M]; int rd[N],q[N]; db f[N]; db c[M]; bool chk[M]; void add(int x,int y) { to[++xnt]=y;nxt[xnt]=hd[x];hd[x]=xnt; } namespace G{ const int M2=(K+M)*2; const db eps=1e-8,jmp=1e-4,INF=3000; int en,hd[M],xnt=1,to[M2],nxt[M2]; db cap[M2]; int cur[M],yhd[M]; db ycap[M2]; int dfn[M],q[M]; vector<int> vt; int dcmp(db x) { if(x>eps)return 1;else if(x<-eps)return -1; return 0; } void add(int x,int y,db z) { to[++xnt]=y;nxt[xnt]=hd[x];hd[x]=xnt;cap[xnt]=z; to[++xnt]=x;nxt[xnt]=hd[y];hd[y]=xnt;cap[xnt]=0; } void init() { for(int i=1,u,v;i<=k;i++) { u=rdn();v=rdn();add(u,v,INF); } en=m+1; } bool bfs() { memset(dfn,0,sizeof dfn); dfn[0]=1; int he=0, tl=0; q[++tl]=0; while(he<tl) { int k=q[++he]; for(int i=hd[k],v;i;i=nxt[i]) { if(dcmp(cap[i])>0&&!dfn[v=to[i]]) { dfn[v]=dfn[k]+1; q[++tl]=v; } } } return dfn[en]; } db dinic(int cr,db flow) { if(cr==en)return flow; db use=0; for(int &i=cur[cr],v;i;i=nxt[i]) if(dcmp(cap[i])>0&&dfn[v=to[i]]==dfn[cr]+1) { db tmp=dinic(v,min(flow-use,cap[i])); if(dcmp(tmp)==0){dfn[v]=0;continue;} use+=tmp; cap[i]-=tmp; cap[i^1]+=tmp; if(dcmp(flow-use)==0)return use; } return use; } db solve() { db l=0,r=n,ans=0; vt.clear();// for(int i=1;i<=m;i++) if(chk[i]) vt.pb(i); memcpy(yhd,hd,sizeof hd); memcpy(ycap,cap,sizeof cap); int yxnt=xnt; while(r-l>jmp) { db mid=(l+r)/2, sm=0; memcpy(hd,yhd,sizeof yhd); memcpy(cap,ycap,sizeof ycap); xnt=yxnt; for(int i=0,lm=vt.size();i<lm;i++) { int cr=vt[i]; db tp=c[cr]-mid; if(dcmp(tp)>0) { sm+=tp; add(0,cr,tp); } else if(dcmp(tp)<0) { add(cr,en,-tp); } } while(bfs()) { memcpy(cur,hd,sizeof hd); sm-=dinic(0,INF); } if(dcmp(sm)>0)ans=mid,l=mid+jmp; else r=mid-jmp; } memcpy(hd,yhd,sizeof yhd);///// memcpy(cap,ycap,sizeof ycap); return ans; } } int main() { n=rdn();m=rdn();k=rdn(); for(int i=1,u,v;i<=m;i++) { u=rdn();v=rdn();add(u,v);rd[v]++; } G::init(); int he=0, tl=0; for(int i=1;i<=n;i++) if(!rd[i])q[++tl]=i; while(he<tl) { int k=q[++he]; for(int i=hd[k],v;i;i=nxt[i]) if((--rd[v=to[i]])==0)q[++tl]=v; } for(int i=n;i;i--) { int cr=q[i]; for(int i=hd[cr];i;i=nxt[i]) { c[i]=f[to[i]]+1; chk[i]=1; } f[cr]=G::solve(); for(int i=hd[cr];i;i=nxt[i]) { chk[i]=0; } } printf("%.10f\n",f[1]); return 0; }
2019.4.9 一题——概率期望+0/1分数规划+最大权闭合子图
标签:+= http names std 技术 一个 using code ems
原文地址:https://www.cnblogs.com/Narh/p/10682395.html