欧拉函数一些定理的证明

标签：没有   设计   html   col   数论   需要   http   数值   while   

参考书籍：《ACM-ICPC程序设计系列--数论及应用》

欧拉函数φ（n）指不超过n且与n互质的正整数的个数，其中n是一个正整数。

欧拉函数的性质：它在整数n上的值等于对n进行素因子分解后，所有的素数上的欧拉函数之积。

定义：

　　1.定义在所有正整数上的函数称为算数函数

　　  2.算法函数f如果满足对任意两个互质的正整数n和m,均有f(mn)=f(n)f(m),就称为积性函数。如果对任意的两个正整数n和m，均有f(mn)=f(m)f(n),就称为完全积性函数。

（欧拉函数就是一个积性函数证明：http://www.cnblogs.com/372465774y/archive/2012/10/16/2726282.html）

定理：

　　1.如果f是一个积性函数，对任意正整数n有素数幂分解n=p₁^a₁  * p₂^a₂  * .... *p_s^a_s,那么f(n)=f(p₁^a₁)*f(p₂^a₂)*...*f(p_s^a_s)。

　　  2.如果p是素数，那么φ(n)=p-1;反之如果p是一个正整数且满足φ(p)=p-1,那么p是素数。　　

　　  3.设p是素数，a是一个正整数，那么φ(p^a)=p^a-p^a-1。

证明：比p^a小的数有p^a-1个，因为p^a只有一个素因子p,其中与p不互质的有p^a-1-1(分别是1*p,2*p,3*p....(p^a-1-1)*p )

所以φ(p^a)=(p^a-1)-(p^a-1-1)=p^a-p^a-1  证毕。

　　  4.设n和m是互质的正整数,那么φ（nm）=φ(n)φ(m)  (因为欧拉函数是积性函数嘛，上面有证明)。

         5.设n=p₁^a₁  * p₂^a₂  * .... *p_k^a_k 为正整数n的素数幂分解，那么

　　　　　　　　φ(n)=n * (1-1/p₁)*(1-1/p₂)*....*(1-1/p_k)  (算法的核心）

证明：由定理4可知φ(n)=φ（p₁^a₁）*φ（p₂^a₂）*.....*φ（p_k^a_k）

　　再由定理3得φ(n)=（p₁^a₁-p₁^a₁-1）*（p₂^a₂-p₂^a₂-1）*.....*（p_k^a_k-p_k^a_k-1）

　　提取因素得φ(n)=p₁^a₁ （1-1/p₁）*p₂^a₂（1-1/p₂）*p_k^a_k（1-1/p_k）

　　所以φ(n)=n * (1-1/p₁)*(1-1/p₂)*....*(1-1/p_k) 证毕。

推论：当n为奇数时，有φ(2n)=φ(n)；

证明：设n=p₁^a₁  * p₂^a₂  * .... *p_k^a_k(假设p1是2)    则 φ(n)=n * (1-1/p₁)*(1-1/p₂)*....*(1-1/p_k)

那么2n=p₁^a₁+1  * p₂^a₂  * .... *p_k^a_k  即φ(2n)=（p₁^a₁+1-p₁^a₁）*（p₂^a₂-p₂^a₂-1）*.....*（p_k^a_k-p_k^a_k-1）

　　　　　　　　　　　　　　　　　　　　　　　　  =p₁^a₁ （p₁-1）*p₂^a₂（1-1/p₂）*p_k^a_k（1-1/p_k）

　　　　　　　　　　　　　　　　　　　　　　　　  =n * （p₁-1）*(1-1/p₂)*....*(1-1/p_k)

　　　　　　　　　　　　　　　　　　　　　　　　  =n *(1-1/p₂)*....*(1-1/p_k)　

因为n为奇数所以没有2这个素因子，即a1=0. 所以φ(n)=n *(1-1/p₂)*....*(1-1/p_k)=φ(2n) 证毕。

         6.设n是一个大于2的正整数，那么φ(n)是偶数

证明：因为φ(n)=（p₁^a₁-p₁^a₁-1）*（p₂^a₂-p₂^a₂-1）*.....*（p_k^a_k-p_k^a_k-1） 

情况一：n有2这个素因子时，p_i^a_i-p_i^a_i-1（令p_i=2）一定是偶数（偶数减偶数嘛）φ(n)是一个偶数的倍数当然是偶数了。

情况二 : n没有2这个素因子，一定存在一个奇素因子，p_i^a_i-p_i^a_i-1为偶数(因为 p^a与p^(a-1) 均为奇数)

　　　　7.∑_d|nφ(d)=n  (即n的因子的欧拉函数值之和为n)

证明：

情况一：n=1时显然成立

情况二：n≠1时，

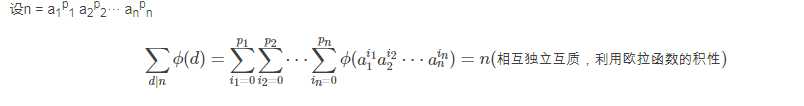
定理基本介绍完了，我们来看代码：

如果根据定理5直接实现：

int phi(int n)
{
    int rea=n;
    for(int i=2;i<=n;i++)
    {
        if(n%i==0)//找到素因子 
        {
            rea=rea/i*(i-1);
            while(n%i==0)//把该素因子全部约掉 
                n/=i;    
        }
    }
    return rea;
}

时间复杂度为O(n)，还可以优化降到O(√n),因为任何一个合数都至少有一个不大于√n的素因子，所以只需要遍历√n即可

int phi(int n)
{
    int rea=n;
    for(int i=2;i*i<=n;i++)//变化的地方 
    {
        if(n%i==0)
        {
            rea=rea/i*(i-1);
            while(n%i==0)
                n/=i;    
        }
    }
    if(n>1)//有可能有一个大于√n素因子 
        rea=rea/n*(n-1);
    return rea;
}

如果最后n>1,为什么一定是一个大于√n的素因子。简单说下，因为不可能是两个及以上素因子的乘积。因为倒数第二个素因子一定小于√n。

欧拉函数一些定理的证明

标签：没有   设计   html   col   数论   需要   http   数值   while   

原文地址：https://www.cnblogs.com/xiongtao/p/10686183.html