标签:bsp 神经网络 com 网络 输入 自组织 时间 语句 过程
1.神经网络工具箱概述
Matlab神经网络工具箱几乎包含了现有神经网络的最新成果,神经网络工具箱模型包括感知器、线性网络、BP网络、径向基函数网络、竞争型神经网络、自组织网络和学习向量量化网络、反馈网络。本文只介绍BP神经网络工具箱。
2.BP神经网络工具箱介绍
BP神经网络学习规则是不断地调整神经网络的权值和偏值,使得网络输出的均方误差和最小。下面是关于一些BP神经网络的创建和训练的名称:
(1)newff:创建一前馈BP网络(隐含层只有一层)
(2)newcf:创建一多层前馈BP网络(隐含层有多层)
(3)train:训练一个神经网络
(4)sim:仿真一个神经网络
以上几个是最主要的语句,在后面的实例应用中会详细说明用法。
3.BP神经网络工具箱在函数逼近中的应用
BP神经网络具有很强的映射能力,主要用于模式识别分类、函数逼近、函数压缩等。下面通过实例来说明BP网络在函数逼近方面的应用。
本文需要逼近的函数是f(x)=1+sin(k*pi/2*x),其中,分别令k=2、3、6进行仿真,设置隐藏层神经元数目为n,n可以改变,便于后面观察隐藏层节点与函数逼近能力的关系。
3.1 k=2,n=5时的仿真实验
先作出目标曲线的图形,以下为matlab代码:
clear all clc %%%%%%%%%%设置网络输入值和目标值%%%%%%%%%% k=2;%f(x)中的k值 x=[-1:.05:8]; f=1+sin(k*pi/2*x); plot(x,f,‘-‘); title(‘要逼近的非线性函数‘); xlabel(‘时间‘); ylabel(‘非线性函数‘);
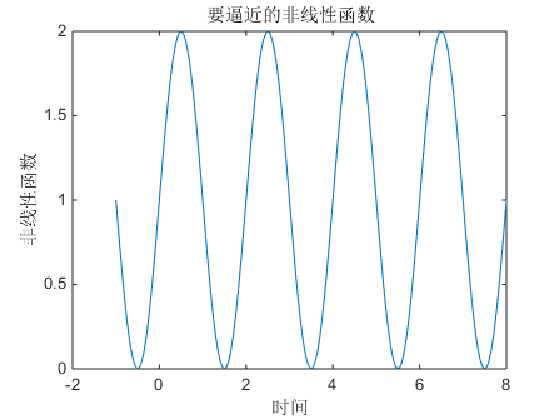
接着用newff函数建立BP神经网络结构,以下为matlab代码:
%%%%%%%%%%建立网络%%%%%%%%%%
n=5;%隐藏层节点数
net = newff(minmax(x),[n,1],{‘tansig‘ ‘purelin‘},‘trainlm‘);
%对于初始网络,可以应用sim()函数观察网络输出。
y1=sim(net,x);
figure;
plot(x,f,‘-‘,x,y1,‘:‘)
title(‘未训练网络的输出结果‘);
xlabel(‘时间‘);
ylabel(‘仿真输出--原函数-‘);
代码中的tansig和purelin分别是输入层到隐藏层和隐藏层到输出层的激活函数,trainlm是训练函数(Levenberg-Marquardt算法训练BP网络)
仿真效果如下:
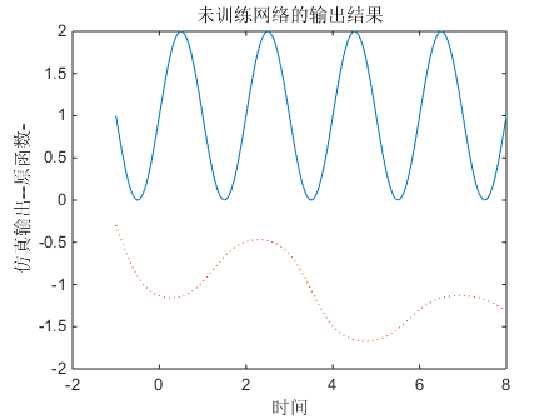
我们可以看到仿真的函数与目标函数相差甚远,这是因为使用newff()函数建立函数网络时,权值和阈值的初始化是随机的,所以网络输出结构很差,根本达不到函数逼近的目的。
因此接下来应用train()函数对网络进行训练后再进行仿真。训练之前,需要预先设置网络训练参数,这里只设置了训练的迭代次数和训练精度,其余参数使用默认值。训练神经网络的matlab代码如下:
%%%%%%%%%%设置训练网络参数%%%%%%%%%%
net.trainParam.epochs=200; %网络最大迭代次数设置为200
net.trainParam.goal=0.2; %网络训练精度设置为0.2
net=train(net,x,f); %开始训练网络;
训练后 得到的误差变化过程如下图所示,可以看出,在运行到第145步时,网络输出误差达到设定的训练精度。
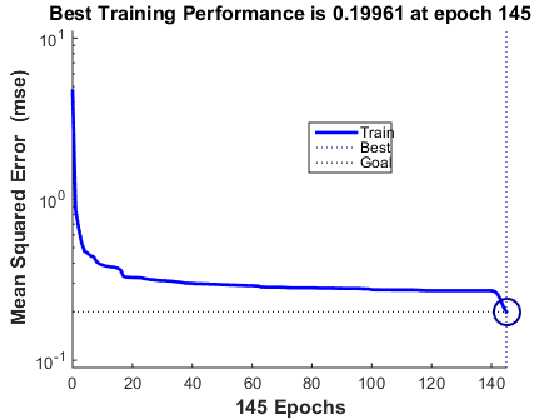
训练好的网络进行仿真,代码如下:
%%%%%%%%%%仿真网络%%%%%%%%%% y2=sim(net,x); figure; plot(x,f,‘-‘,x,y1,‘:‘,x,y2, ‘--‘) title(‘训练后网络的输出结果‘); xlabel(‘时间‘); ylabel(‘仿真输出‘);
绘制网络输出曲线,与目标曲线和未训练网络的输出结果相比较,如下图所示:
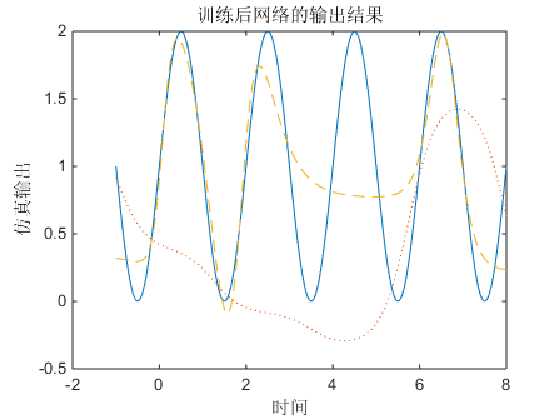
由此可以看出,与未训练的曲线相比,经过训练之后的曲线和目标曲线更接近,这说明BP网络对非线性函数的逼近效果比较好。
接下来通过改变隐藏层的节点数来看其对网络逼近的效果
3.2 k=2,n=3、n=10时的仿真实验
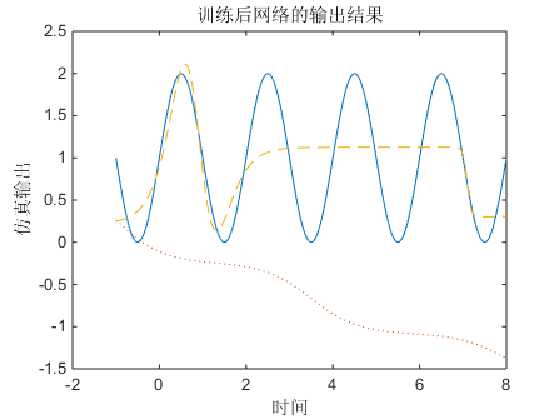
将隐藏层节点数改为3,其他条件不变,仿真效果如下:
将隐藏层节点数改为10,其他条件不变,仿真效果如下:
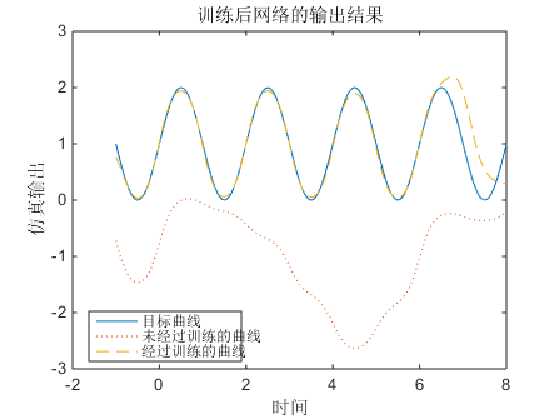
由以上两张图可以看出,当n=10时,经过训练后的曲线基本跟目标曲线重合;当n=3时,逼近效果却很差,这说明改变隐藏层节点数对函数逼近的效果有一定影响。
4.总结
一般来说,隐藏层神经元数目越多,则BP网络逼近非线性函数的能力越强。由于本例中单隐含层的输入层和输出层神经元个数均为1,那么隐含层的个数可以根据设计
经验公式和该问题的实际情况相结合,通过实验选取最好的隐藏层节点数,使得逼近效果最佳。

标签:bsp 神经网络 com 网络 输入 自组织 时间 语句 过程
原文地址:https://www.cnblogs.com/DLB511/p/10693386.html