标签:函数 部分 code com 不难 info ... 自己 例题
数论卷积:
对于两个数论函数f(x),g(x)
f(n)g(n)=∑ f(d)g(n/d)
d|n


莫比乌斯函数:
设一个数n=(p1^k1)*(p2^k2)*(p3^k3)*..........*(pn^kn)
/ 1,n=1
则μ(n)= 0,max(k1,...kn)=1
\ -1^r ,max(k1......kn)=r,r>1
莫比乌斯函数有个性质:
∑ μ(d)在n为1时为1,其余时为0
d|n
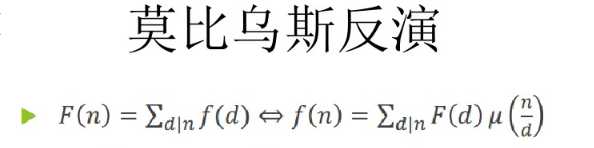


例题:给定a,b,c,d,在a≤x≤c,b≤y≤d中,求满足gcd(x,y)=1的(x,y)

这样,我们就可以把要求的x,y视为一个二维前缀和,即:
[1≤x≤c,1≤y≤d]-[1≤x≤a,1≤y≤d]-[1≤x≤c,1≤y≤b]+[1≤x≤a,1≤y≤b](就是上图红色部分的面积=总面积-a*d的矩形-c*b的矩形+a*b的矩形)
那么每一部分就可以表示为求起点为1,x的终点为n,y的终点为m的式子
如下:
n m
∑ ∑ [gcd(i,j)]=1
i=1 j=1
这里中括号的意思是:若括号内为真,返回1,若为假,返回0
∑计算有一下几种性质:
1.交换两个∑,结果不变
2.将某个∑后面与当前∑枚举的东西无关的式子提到该∑前面来,结果不变
显然枚举原式可以枚举到地老天荒(显然我们要化简)
联系一下前面莫比乌斯函数的性质:
∑ μ(d)在n为1时为1,其余时为0
d|n
不难发现,原式可以写成这样:
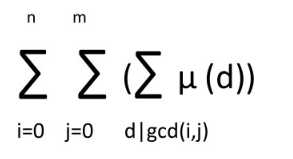
显然这里确定i,j枚举d不好枚举,那我们换过来,确定d枚举i,j
n
∑ ∑ ∑ μ(d)
d=1 ad=i, bd=j,
i<=n j<=m
这时候,μ(d)与前两个∑没有关系,那就把它提到前面来
n
∑ μ(d) ∑ ∑
d=1 ad=i, bd=j,
i<=n j<=m
后面两个∑可视为枚举1到n和1到m中d的倍数。1到n中d的倍数有 ![]() 个,1到m中d的倍数有
个,1到m中d的倍数有![]() 个
个

一个式子解决了。
剩下的就是将二维前缀和中的式子往里带了
嗯虽然不知道自己写了些什么,但先记下来以后慢慢看
标签:函数 部分 code com 不难 info ... 自己 例题
原文地址:https://www.cnblogs.com/lcez56jsy/p/10686260.html