标签:code 遍历 com cte his public 返回 void src
1. 图的表示:
1)邻接矩阵:
a. 表示无向图:
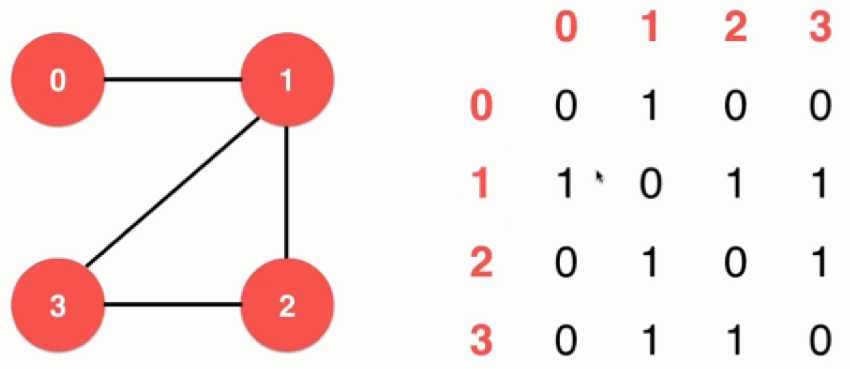
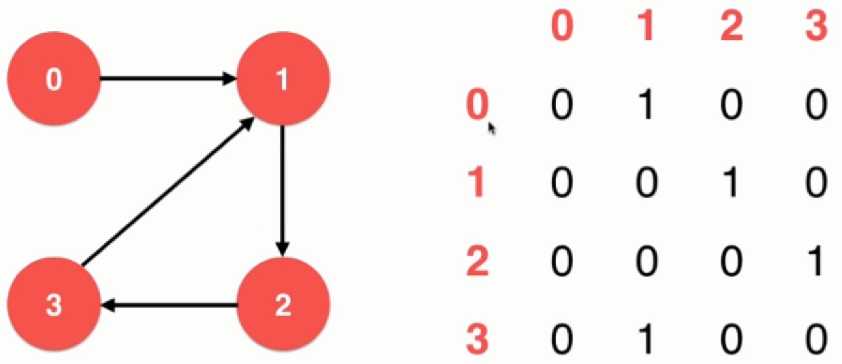
b. 表示无向图:
#include<stdio.h> #include<stdlib.h> #include<vector> #include<iostream> #include<assert.h> using namespace std; //稠密图 - 邻接矩阵 class DenseGraph { private: int n, m; //顶点,边 bool directed; //有向或无向 vector<vector<bool>> g; //邻接矩阵 public: DenseGraph(int n, bool directed) { this->n = n; this->m = 0; this->directed = directed; for (int i = 0; i < n; i++) { g.push_back(vector<bool>(n, false)); } } ~DenseGraph() { } int V() { return n; } int E() { return m; } void addEdge(int v, int w) { assert(v >= 0 && v < n); assert(w >= 0 && w < n); if (hasEdge(v, w)) return; //若已经有边,直接return g[v][w] = true; //有向图 if (!directed) { //无向图 g[w][v] = true; } m++; } bool hasEdge(int v, int w) { //判断v和w之间是否已经存在边 (不包括平行边) assert(v >= 0 && v < n); assert(w >= 0 && w < n); return g[v][w]; //返回为true或false } };
2)邻接表:
a. 无向图:
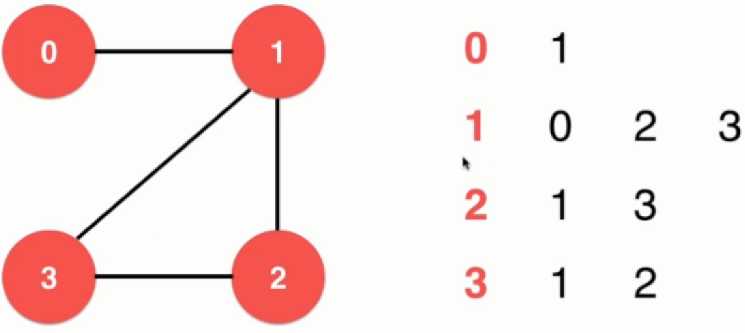
第一行:0 和 1 相连;
第二行:1 和 0,2,3 相连;
第三行:2 和 1,3 相连;
第四行:3 和 1,2 相连。
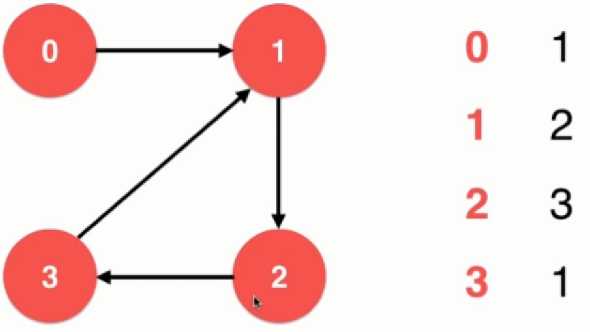
b. 有向图:
邻接表适合表示一个稀疏的图, 邻接矩阵适合表示一个稠密的图。
若有平行边,邻接表会最多需要O(n)的时间复杂度, 去把平行边消除。
#include<stdio.h> #include<stdlib.h> #include<vector> #include<iostream> #include<assert.h> using namespace std; //稀疏图 - 邻接表 class SparseGraph { private: int n, m; //顶点,边 bool directed; //有向或无向 vector<vector<int>> g; // 邻接表 每一行存储的是顶点编号 public: SparseGraph(int n, bool directed) { //构造函数来初始化 this->n = n; this->m = 0; this->directed = directed; for (int i = 0; i < n; i++) { g.push_back(vector<int>() ); } } ~SparseGraph() { } int V() { return n; } int E() { return m; } void addEdge(int v, int w) { assert(v >= 0 && v < n); assert(w >= 0 && w < n); if (hasEdge(v, w)) return; //若已经有边,直接return g[v].push_back(w); //v和w相连 if (v!=w && !directed) { //无向图 g[w].push_back(v); } m++; } bool hasEdge(int v, int w) { //判断v和w之间是否存在边 assert(v >= 0 && v < n); //判断v和w不越界 assert(w >= 0 && w < n); for (int i = 0; i < g[v].size();i++) { if (g[v][i] == w) return true; return false; } return g[v][w]; //返回为true或false } };
2. 遍历邻边

邻接矩阵需要O(v)的时间复杂度,v为顶点个数。
所以最好使用邻接表。
标签:code 遍历 com cte his public 返回 void src
原文地址:https://www.cnblogs.com/Bella2017/p/10700712.html