标签:方法 方向 href aik 生成 问题 baidu 中间 targe
图论是应用广泛的运筹学分支,在实际生活、生产和科学研究中,有很多问题可以用图论的理论和方法来解决。
经典的图论问题有:欧拉七桥问题、环球旅行问题、中国邮递员问题......
欧拉回路:从图中任意一点出发,经过图中所有边一次且仅一次的回路。
哈密顿回路:从图中任意一点出发,经过图中所有顶点一次且仅一次的回路。
中国邮递员问题:
一名邮递员负责投递某个街区的邮件。如何为他(她)设计一条最短的投递路线?(从邮局出发,经过投递区内每条街道至少一次,最后返回邮局)由于这一问题是我国管梅谷教授1960年首先提出的,所以国际上称之为中国邮递员问题。
(仅供科普,以后有机会单独写一篇)
点数p、边数q、关联边、环、多重边、点的次(度)d(v)、奇点、偶点、悬挂点、孤立点、悬挂边
相关定理:①任一图中,所有点的次之和是边数的两倍(即度数之和为2q)。②任一图中,奇点的个数为偶数。
链:图中的点、边交错的序列。(初等链:所有点均不相同的链简单链:所有边均不相同的链。)
圈:两个端点相同的链。
中间点:除了两个端点以外的点。
基础图G(D):从有向图D中去掉所有弧的箭头得到的无向图。
始点、终点、弧
路:一条按照弧方向前进的链。
回路:起、终点相同;初等路:各顶点不相同的路
1. 树:一个无圈的连通图。
如:
2. 树的6个等价性质:
设图 T = (V, E)是一个树,其中点数为p、边数q
(1)T为无圈的连通图
(2)T无圈,且q=p-1
(3)T连通,且q=p-1
(4)T无圈,但增加一条边,可得到一个且仅一个圈
(5) T连通,但舍弃一条边,图便不连通
(6)T中任意两个顶点之间恰有一条链
3. 生成树(支撑树):若T=(V,E′)是G=(V,E)的生成子图,且T是一个树,则T为G的一个生成树。
图G有生成树的充要条件是图G是连通的。
证明:
必要性是显然的。
充分性 设G是连通图,若G不含圈,则G本身是一个树,从而G是它自身的一个支撑树。若G含圈,任取一个圈,从圈中去掉任意一条边,得到G的一个支撑子图G1。若G1不含圈,则G1是G的一个支撑树;否则继续上述破圈操作,直到没有圈为止,最终找到一个支撑子图,它不含圈,是G的一个支撑树。
寻找生成树的方法:“破圈法”和“避圈”法
破圈法:破坏已有的圈。
避圈法:连接点的时候避免构成圈。
所以生成树对于连通图来说是不唯一的。
4. 赋权图:给图G=(V,E),对G中的每一条边[vi, vj],相应地有一个数wij,则称这样的图G为赋权图,wij称为边[vi, vj]上的权。
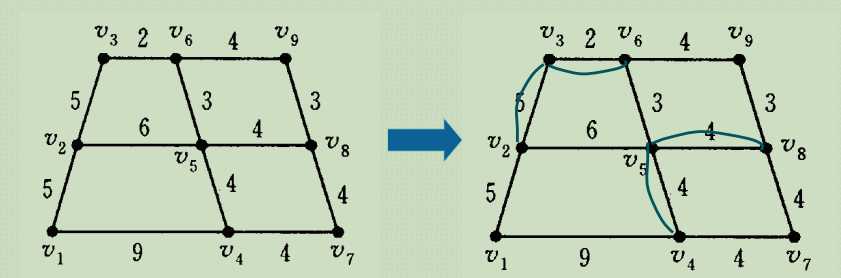
5. 最小生成树:T = (V, E′)是G的一个生成树,T中所有边的权之和为生成树的权w(T)。如果T*的权w(T*)是G的所有生成树的权中最小者,则称为G的最小生成树树(最小树)
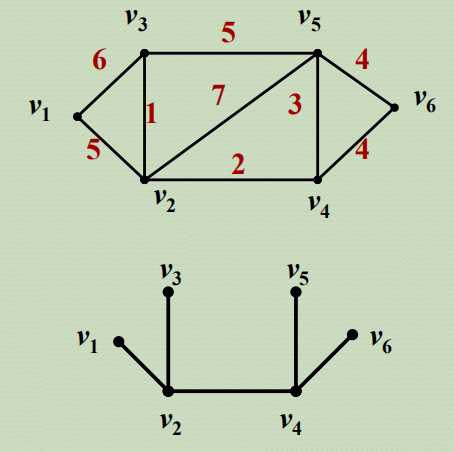
6. 最小树问题:
例:某工厂在6个车间之间的道路网如图所示,每条道路的距离已知。
问:如何沿道路架设电话线网,才能使电话线的总长最小?
最小树问题就是在赋权图上求最小生成树的问题

避圈法操作起来相对比较麻烦。
例:
最短路问题是在赋权有向图中寻求最短路的问题。
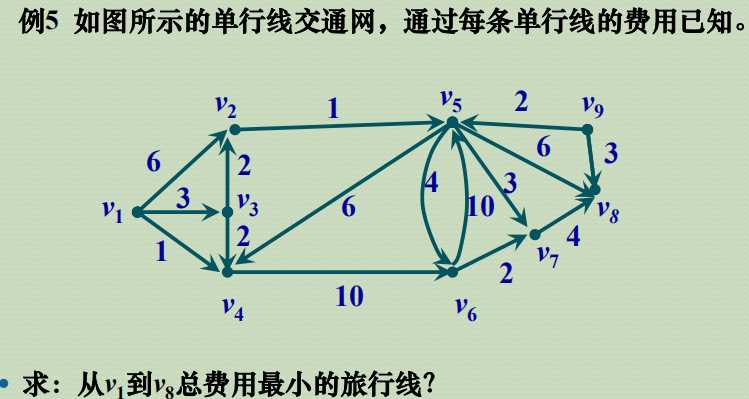
求解方法:Dijkstra算法
适用范围:正费用网络(wij ≥ 0),即权值不为负。
基本步骤:


问题引入:
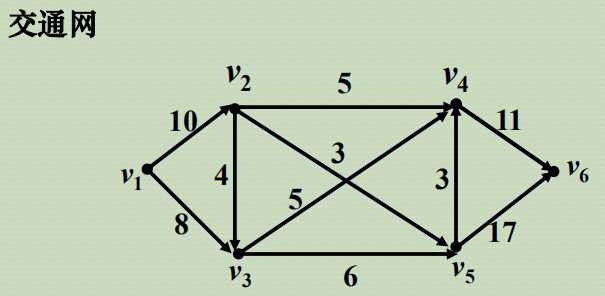
要求制定一个运输方案使从v1到v6运输的产品数量最多。
基本概念:
网络:给定一个有向图D = (V,A),在V中指定一点为发点(始点),记为vs,而另一点为收点(终点),记为vt,其余点为中间点。对于每一个弧(vi,vj) ∈A ,对应有一个c(vi,vj)≥0,简写为cij,称为弧的容量。这样的D叫做一个网络,记为D = (V, A, C)
流:所谓网络上的流是指定义在弧集合A上的一个函数f = {f(vi,vj)},并称f(vi,vj)为弧(vi,vj)的流量,简称fij。
可行流:

零流:令所有弧的流量fij=0,就得到一个零流,其流量v(f)=0。
最大流: 使流量v(f)最大的可行流。
最大流问题的数学模型:
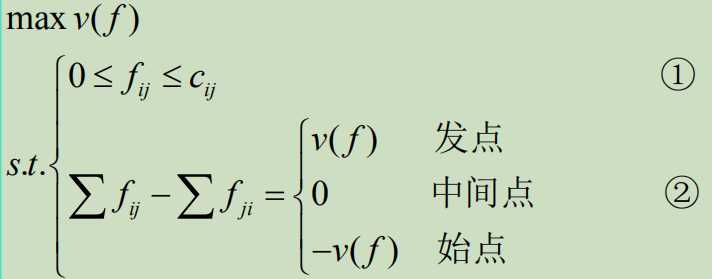
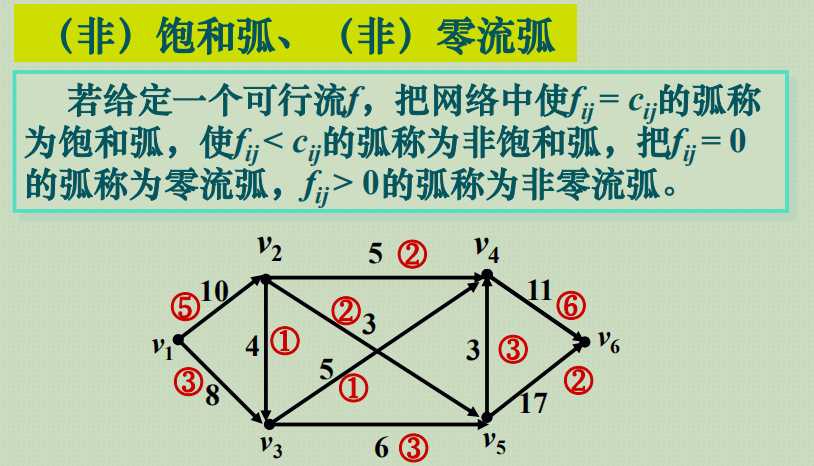
(非)饱和弧、(非)零流弧:
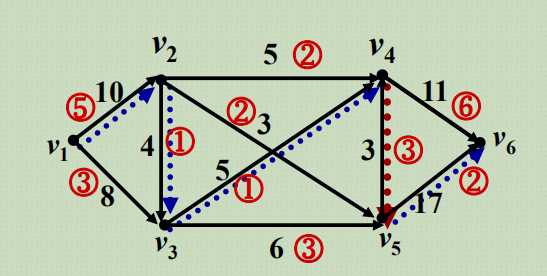
向前弧、向后弧:

标签:方法 方向 href aik 生成 问题 baidu 中间 targe
原文地址:https://www.cnblogs.com/fangxiaoqi/p/10566717.html