标签：mes   dig   read   algo   template   oid   swa   code   open   

题目链接

题意分析

首先考虑链的话 就是将\(1\)部分的两条子链排序之后 贪心合并即可

那么考虑树的话

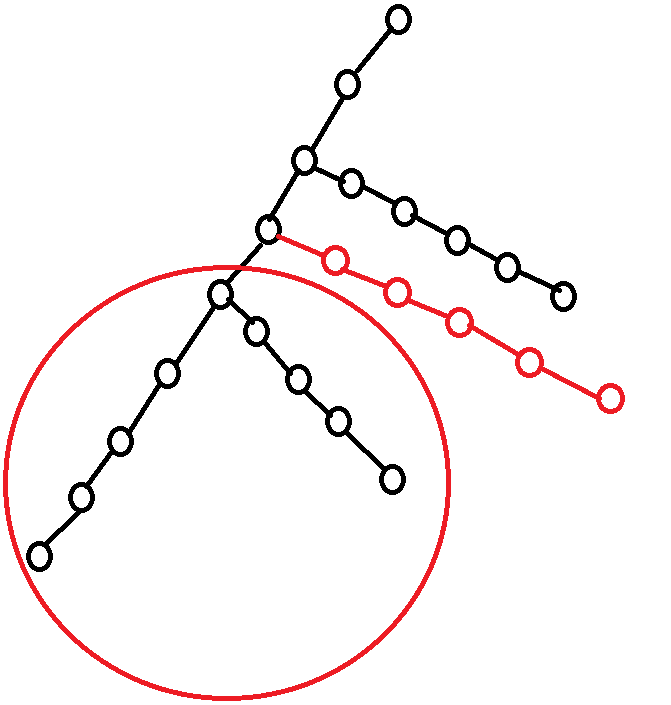
我们照样合并就行了

首先 排序的话 我们使用堆就可以了

然后 涉及到了两点问题

\(1.\)我们对于\(u\)以及\(v\)这两个维护好的堆合并的话

为了保证时间复杂度 我们需要使用启发式合并

\(2.\)我们由于启发式合并的话涉及到了交换两个堆的问题

听巨佬说

c++11的话 直接swap是\(O(1)\)的

否则的话 直接\(swap\)就是\(O(n)\)

所以我们考虑维护新的编号 然后直接交换编号就可以了

CODE:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<cstdlib>
#include<string>
#include<queue>
#include<map>
#include<stack>
#include<list>
#include<set>
#include<deque>
#include<vector>
#include<ctime>
#define ll long long
#define inf 0x7fffffff
#define N 500008
#define IL inline
#define M 1008611
#define D double
#define ull unsigned long long
#define R register
using namespace std;
template<typename T>IL void read(T &_)
{
    T __=0,___=1;char ____=getchar();
    while(!isdigit(____)) {if(____=='-') ___=0;____=getchar();}
    while(isdigit(____)) {__=(__<<1)+(__<<3)+____-'0';____=getchar();}
    _=___ ? __:-__;
}
/*-------------OI使我快乐-------------*/
int n,m,tot;
int to[N],nex[N],head[N],num[N],id[N];
ll ans,tmp[N];
priority_queue<ll> Q[N>>1];
IL void add(int x,int y)
{to[++tot]=y;nex[tot]=head[x];head[x]=tot;}
IL void dfs(int now)
{
    id[now]=++tot;
    for(R int i=head[now];i;i=nex[i])
    {
        int v=to[i];
        dfs(v);
    }
    for(R int i=head[now];i;i=nex[i])
    {
        int v=to[i];
        if(Q[id[now]].size()<Q[id[v]].size()) swap(id[now],id[v]);//直接交换编号
        int tmp_size=Q[id[v]].size();
        for(R int j=1;j<=tmp_size;++j)
        {
            tmp[j]=max(Q[id[now]].top(),Q[id[v]].top());
            Q[id[now]].pop();Q[id[v]].pop();
        }
        for(R int j=1;j<=tmp_size;++j) Q[id[now]].push(tmp[j]);  
    }
    Q[id[now]].push(num[now]);
}
int main()
{
//  freopen(".in","r",stdin);
//  freopen(".out","w",stdout);
    read(n);
    for(R int i=1;i<=n;++i) read(num[i]);
    for(R int i=2,x;i<=n;++i)
    {
        read(x);add(x,i);
    }
    tot=0;dfs(1);
    while(!Q[id[1]].empty()) ans+=Q[id[1]].top(),Q[id[1]].pop();
    printf("%lld\n",ans);
//  fclose(stdin);
//  fclose(stdout);
    return 0;
}

P5290 [十二省联考2019]春节十二响

标签：mes   dig   read   algo   template   oid   swa   code   open   

原文地址：https://www.cnblogs.com/LovToLZX/p/10726019.html