【剑指Offer】4、重建二叉树

标签：递归   前序遍历   while   位置   构建   ret   树的遍历   n+1   遍历   

??题目描述：

??输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回根结点。

??解题思路：

??树的遍历有三种：分别是前序遍历、中序遍历、后序遍历。本题是根据前序和中序遍历序列重建二叉树，我们可以通过一个具体的实例来发现规律，不难发现：前序遍历序列的第一个数字就是树的根结点。在中序遍历序列中，可以扫描找到根结点的值，则左子树的结点都位于根结点的左边，右子树的结点都位于根结点的右边。

??这样，我们就通过这两个序列找到了树的根结点、左子树结点和右子树结点，接下来左右子树的构建可以进一步通过递归来实现。

??举例：

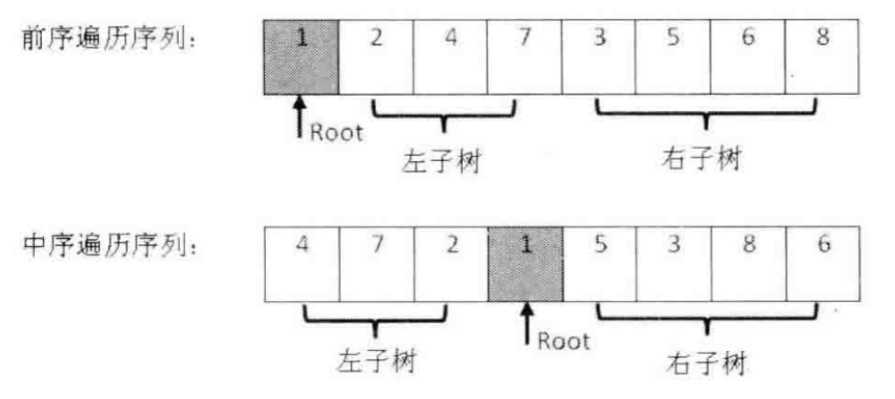
??编程实现（Java）：

    public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
        /*根据前序遍历和中序遍历确定一棵二叉树*/
        //递归实现
        if(pre==null||in==null||pre.length==0)
            return null;
        return reConstructBinaryTree(pre,in,0,pre.length-1,0,in.length-1);
    }
    public TreeNode reConstructBinaryTree(int [] pre,int [] in,int pre_begin,
                                          int pre_end,int in_begin,int in_end)
    {
        ////前序序列：从pre_begin到pre_end,  中序序列：从in_begin到in_end
        //递归结束条件
        if(pre_begin>pre_end || in_begin>in_end)
            return null;
        
        int rootValue=pre[pre_begin];
        TreeNode root=new TreeNode(rootValue);  //第一个节点就是根节点
        if(pre_begin==pre_end || in_begin==in_end)
            return root;
        //在中序序列中，找到root，前面的就是左子树，右边的就是右子树
        int rootIn=in_begin; //root在中序序列中的位置
        while(rootIn<=in_end && in[rootIn]!=rootValue)
            rootIn++;
        
        int left_count=rootIn-in_begin; //左子树节点个数                                   
        root.left=reConstructBinaryTree(pre,in,pre_begin+1,pre_begin+left_count,
                                   in_begin,rootIn-1);
        root.right=reConstructBinaryTree(pre,in,pre_begin+left_count+1,
                                       pre_end,rootIn+1,in_end);
        return root;
    }

【剑指Offer】4、重建二叉树

标签：递归   前序遍历   while   位置   构建   ret   树的遍历   n+1   遍历   

原文地址：https://www.cnblogs.com/gzshan/p/10730338.html