标签:hduoj -- 不能 中文 display 花生 范围 opened 区间
二维差分和一维差分思路上并没有什么区别,具体实现的区别就在于一维的直接对区间两端差分就好了,而二维的多了一维需要处理。
差分的思想是和前缀和有关的,一维的前缀和我们都懂求,那么二维的呢?
如图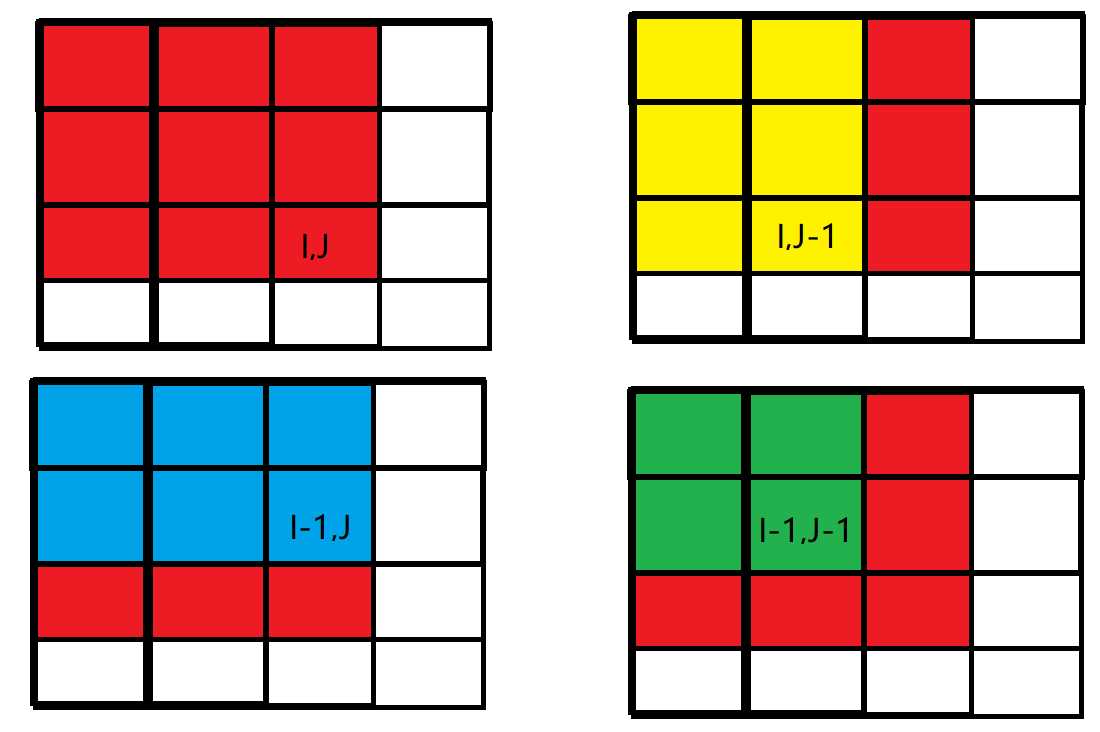
因为是从左到右,从上到下的遍历,当要求红色部分,(0,0)到(i,j)处的前缀和时,我们黄色部分和蓝色部分已经是已知的了,而它们重叠的部分就是绿色部分,所以把黄色和蓝色部分的结果加起来,再减去绿色部分,最后加上(i,j)处的值就是(i,j)位置的前缀和了。
所以,二维前缀和就是sum[i][j]=a[i][j]+sum[i-1][j]+sum[i][j-1]+sum[i-1][j-1]
而我们要求左上角是(x1,y1),右下角是(x2,y2)的矩形区间内的值处理出前缀和后也可以O(1)时间内求出来。
如图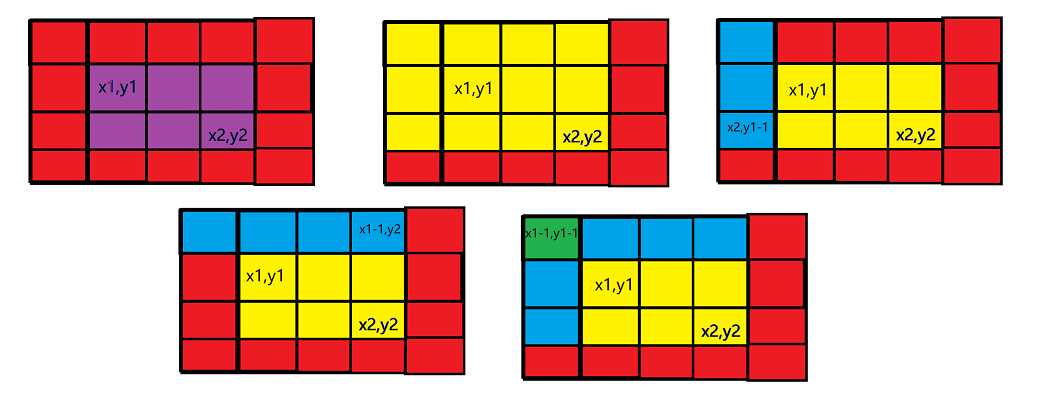
我们要求紫色部分的值,我们已知的是黄色部分的值,但它多了两个蓝色部分的值,而两个蓝色部分有重叠了个绿色部分
所以要求的区间内的值就是sum[x2][y2]-sum[x2][y1-1]+sum[x1-1][y2]+sum[x1-1][x2-1]
中文题,二维前缀和的练手题。

1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 typedef long long ll; 5 ll sum[1018][1018]={0}; 6 int main() 7 { 8 int n,m,l,w; 9 while(~scanf("%d%d",&n,&m)) 10 { 11 for(int i=1;i<=n;i++) 12 for(int j=1;j<=m;j++) 13 scanf("%lld",&sum[i][j]); 14 for(int i=1;i<=n;i++) 15 for(int j=1;j<=m;j++) 16 sum[i][j]+=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]; 17 scanf("%d%d",&l,&w); 18 ll ans=0; 19 //题目给的l,w不是说(0,0)到(l,w)的矩形 20 //而是长为l,宽为w的矩形 21 //枚举左上角 22 for(int x1=1;x1<=n;x1++) 23 for(int y1=1;y1<=m;y1++) 24 { 25 int x2=x1+l-1,y2=y1+w-1; 26 if(x2<=n&&y2<=m)//右下角在范围内 27 ans=max(ans,sum[x2][y2]-sum[x2][y1-1]-sum[x1-1][y2]+sum[x1-1][y1-1]); 28 } 29 printf("%lld\n",ans); 30 } 31 return 0; 32 }
照这样画图的方法我们,也可以得出差分值的放置位置,一维时是在需要更新的位置开始,不需要的位置结束,而二维的也一样。
如果我们要在左上角是(x1,y1),右下角是(x2,y2)的矩形区间每个值都+a
如图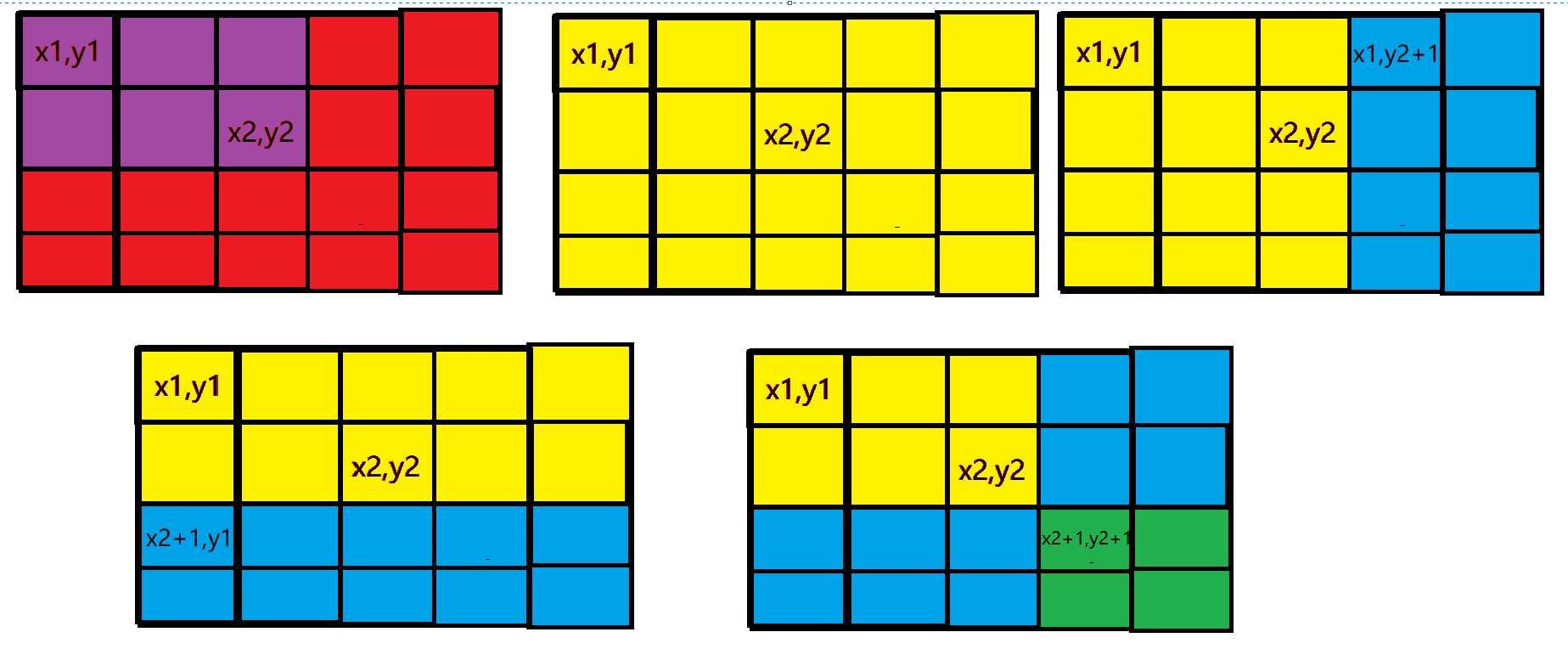
在我们要的区间开始位置(x1,y1)处+a,根据前缀和的性质,那么它影响的就是整个黄色部分,多影响了两个蓝色部分,所以在两个蓝色部分-a消除+a的影响,而两个蓝色部分重叠的绿色部分多受了个-a的影响,所以绿色部分+a消除影响。
所以就是dif[x1][y1]+=a,dif[x1][y2+1]-=a,dif[x2+1][y1]-=a,dif[x2+1][y2+1]+=a
这道让我开始学差分的题。。。
题目大意:先给出一个n*m的范围,然后给出p个监控矩形的左下角和右上角,最后有q个询问,问给出左下角和右上角的矩形是否完全被监控到。
没学差分之前一直想用线段树来维护来做,但很麻烦根本不会做,而学了差分之后,因为p个矩形是已经选给出了,所以我们可以离线处理这些矩形,类似于一维的那道牛客的区间覆盖的问题,我们dif的差分数组可以得出(i,j)这个位置被多少个监控监控到,然后我们让被监控到的点权值为1,然后维护一个被监控到的点数的前缀和,那么询问的矩形要是被监控到的点等于面积,那么就是yes,否则就是no,恶心的地方就在于这题不能开二维数组,需要降维处理。

1 #include<cstdio> 2 const int N=13142118; 3 int dif[N],cov[N]; 4 //cov被监控到的点的前缀和 5 int main() 6 { 7 int n,m,p,q,x1,y1,x2,y2; 8 while(~scanf("%d%d",&n,&m)) 9 { 10 for(int i=0;i<n;i++) 11 for(int j=0;j<m;j++) 12 { 13 dif[i*m+j]=0; 14 cov[i*m+j]=0; 15 } 16 scanf("%d",&p); 17 while(p--) 18 { 19 scanf("%d%d%d%d",&x1,&y1,&x2,&y2); 20 x1--,y1--,x2--,y2--; 21 dif[x1*m+y1]++; 22 if(x2+1<n) 23 dif[(x2+1)*m+y1]--; 24 if(y2+1<m) 25 dif[x1*m+y2+1]--; 26 if(x2+1<n&&y2+1<m) 27 dif[(x2+1)*m+(y2+1)]++; 28 } 29 for(int i=0;i<n;i++) 30 { 31 for(int j=0;j<m;j++) 32 { 33 if(i) 34 dif[i*m+j]+=dif[(i-1)*m+j]; 35 if(j) 36 dif[i*m+j]+=dif[i*m+j-1]; 37 if(i&&j) 38 dif[i*m+j]-=dif[(i-1)*m+j-1]; 39 //如果这个位置有被监控到就是设为1 40 if(dif[i*m+j]>=1) 41 cov[i*m+j]=1; 42 else 43 cov[i*m+j]=0; 44 if(i) 45 cov[i*m+j]+=cov[(i-1)*m+j]; 46 if(j) 47 cov[i*m+j]+=cov[i*m+j-1]; 48 if(i&&j) 49 cov[i*m+j]-=cov[(i-1)*m+j-1]; 50 } 51 } 52 // for(int i=n-1;i>=0;i--) 53 // { 54 // for(int j=0;j<m;j++) 55 // if(dif[i*m+j]>=1) 56 // printf("1 "); 57 // else 58 // printf("0 "); 59 // printf("\n"); 60 // } 61 scanf("%d",&q); 62 while(q--) 63 { 64 scanf("%d%d%d%d",&x1,&y1,&x2,&y2); 65 int area=(x2-x1+1)*(y2-y1+1),cova=0; 66 x1--,y1--,x2--,y2--; 67 cova+=cov[x2*m+y2]; 68 if(x1-1>=0) 69 cova-=cov[(x1-1)*m+y2]; 70 if(y1-1>=0) 71 cova-=cov[x2*m+y1-1]; 72 if((x1-1)>=0&&(y1-1)>=0) 73 cova+=cov[(x1-1)*m+(y1-1)]; 74 // printf("%d %d\n",area,cova); 75 if(area==cova) 76 printf("YES\n"); 77 else 78 printf("NO\n"); 79 } 80 } 81 return 0; 82 }
NOIAC#71画画鬼才
标签:hduoj -- 不能 中文 display 花生 范围 opened 区间
原文地址:https://www.cnblogs.com/LMCC1108/p/10753451.html