汉诺塔问题

汉诺塔问题是一个经典的问题。汉诺塔（Hanoi Tower），又称河内塔，源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，任何时候，在小圆盘上都不能放大圆盘，且在三根柱子之间一次只能移动一个圆盘。问应该如何操作？

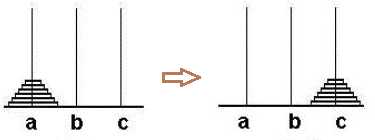
分解问题

一股脑地考虑每一步如何移动很困难，我们可以换个思路。先假设除最下面的盘子之外，我们已经成功地将上面的63个盘子移到了b柱，此时只要将最下面的盘子由a移动到c即可。如图：

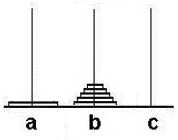
当最大的盘子由a移到c后，b上是余下的63个盘子，a为空。因此现在的目标就变成了将这63个盘子由b移到c。这个问题和原来的问题完全一样，只是由a柱换为了b柱，规模由64变为了63。因此可以采用相同的方法，先将上面的62个盘子由b移到a，再将最下面的盘子移到c……对照下面的过程，试着是否能找到规律：

递归方法程序实现

def hannoi(n,a,b,c):
    if n>0:
        hannoi(n-1,a,c,b)   #a移动到c  b为辅助
        print(‘moving from %s to %s‘%(a,c))
        hannoi(n-1,b,a,c)　　#b移动到a  c为辅助




如果将这个问题的盘子数量减为10个或更少，就不会有太大的问题了。但盘子数量为64的话，你一共需要移动约1800亿亿步（18,446,744,073,709,551,615），
才能最终完成整个过程。这是一个天文数字，没有人能够在有生之年通过手动的方式来完成它。即使借助于计算机，假设计算机每秒能够移动100万步，那么约需要18万亿秒，
即58万年。将计算机的速度再提高1000倍，即每秒10亿步，也需要584年才能够完成。

关于递归的四条基本法则
1.基准情形。必须有某些基准情形，它无需递归就能解出。
2.不断推进。对于那些需要递归求解的情形，每一次递归调用都必须要使求解的状况朝接近基准情形的方向推进。
3.设计法则。假设所有的递归调用都能运行。
4.合成效益法则。在求解同一个问题的同一实例时，切勿在不同的递归调用中做重复性的工作 

---------------------