标签:数据结构 最大值 ble org 执行 最小堆 第一个 重建 图片
原题链接 https://www.luogu.org/problemnew/show/P1090
看了题面,应该就会想到用贪心+二叉堆吧。
先带大家走一遍思路:
题目要求消耗的最小体力值,很轻易就想到每次找两个最小的堆进行合并,重复n-1次,那么这样消耗的体力一定是最少的,贪心思想!
对于排序,我们更轻易得想到用sort排序,每次取出最小的两个元素就好啦;
然后就像我一样用sort快排交了上去,发现TLE了一堆!!!
为什么呢???
sort排序固然很快!但是对于n-1排序的话,就远远不如堆排序了。堆排序运用了二分的思想,大大缩短了排序时间!
二分思想?如果不了解堆排序的你现在可能有点懵,下面解释一下堆排序的原理及代码实现吧: 详细请看大佬的博客https://www.cnblogs.com/chengxiao/p/6129630.html qaq~
堆排序
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为O(nlogn),它也是不稳定排序。首先简单了解下堆结构。
堆
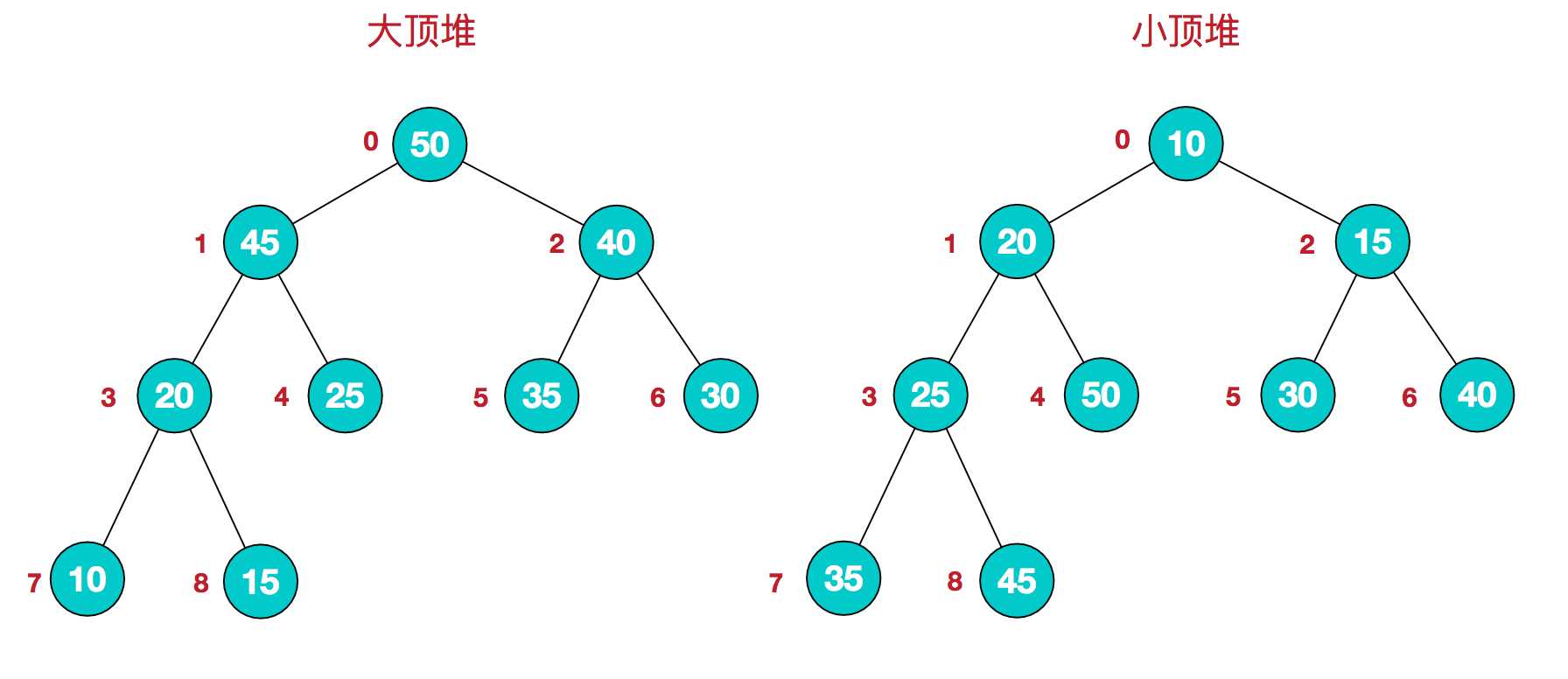
堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。如下图:
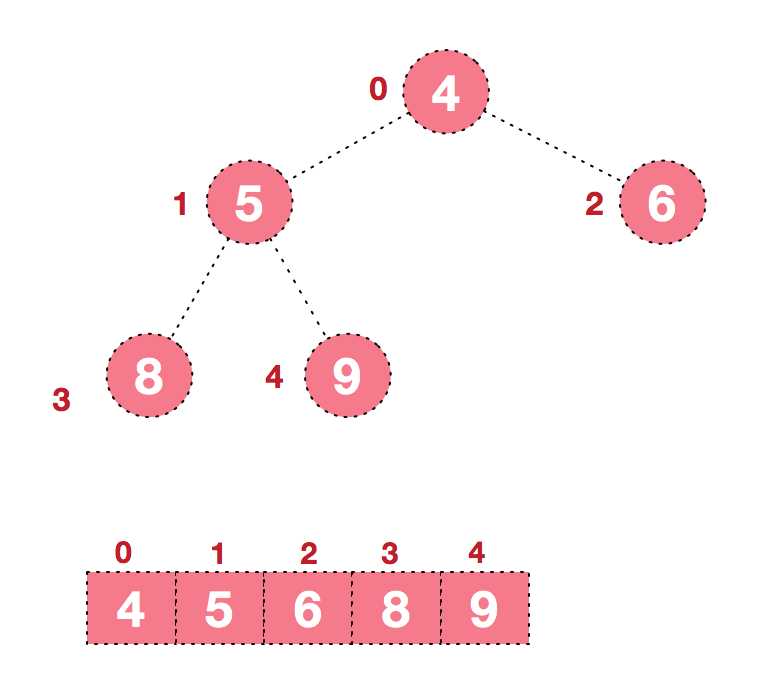
同时,我们对堆中的结点按层进行编号,将这种逻辑结构映射到数组中就是下面这个样子

该数组从逻辑上讲就是一个堆结构,我们用简单的公式来描述一下堆的定义就是:
大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
ok,了解了这些定义。接下来,我们来看看堆排序的基本思想及基本步骤:
堆排序的基本思想是:将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了
步骤一 构造初始堆。将给定无序序列构造成一个大顶堆(一般升序采用大顶堆,降序采用小顶堆)。
a.假设给定无序序列结构如下
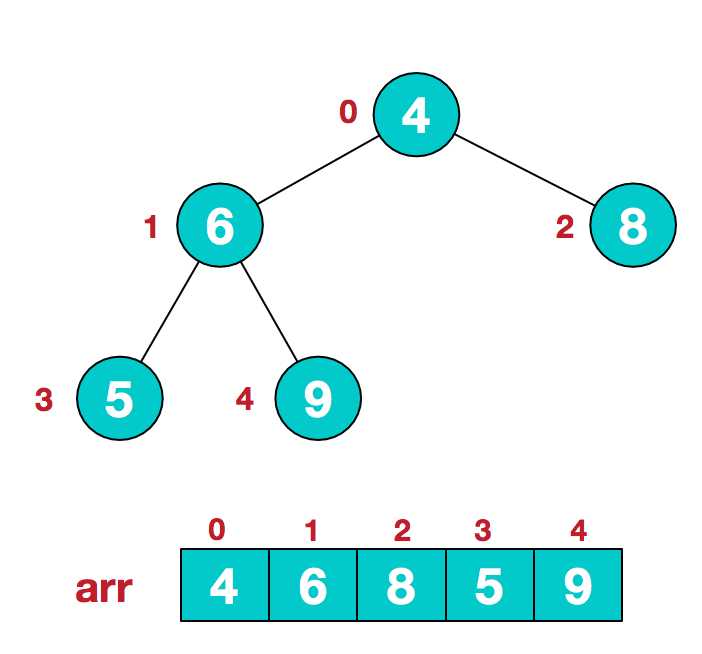
2.此时我们从最后一个非叶子结点开始(叶结点自然不用调整,第一个非叶子结点 arr.length/2-1=5/2-1=1,也就是下面的6结点),从左至右,从下至上进行调整。
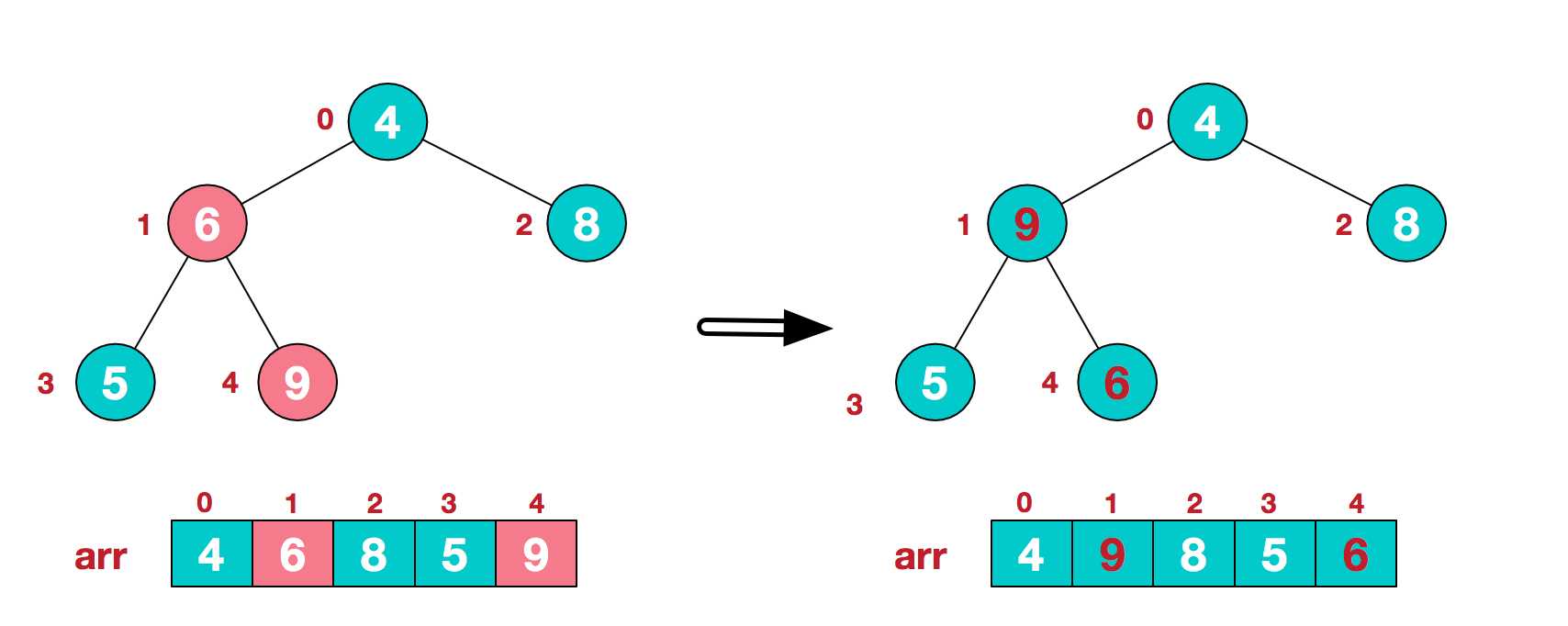
4.找到第二个非叶节点4,由于[4,9,8]中9元素最大,4和9交换。
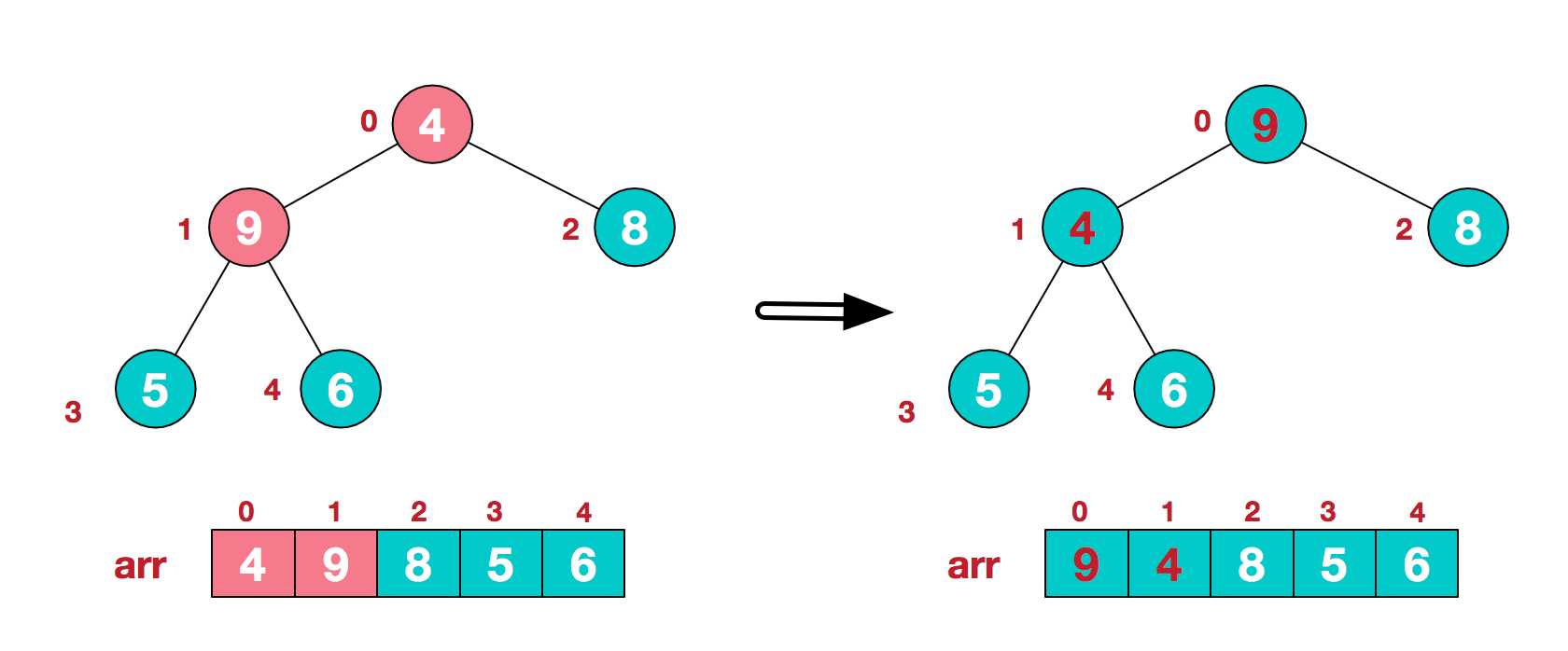
这时,交换导致了子根[4,5,6]结构混乱,继续调整,[4,5,6]中6最大,交换4和6。
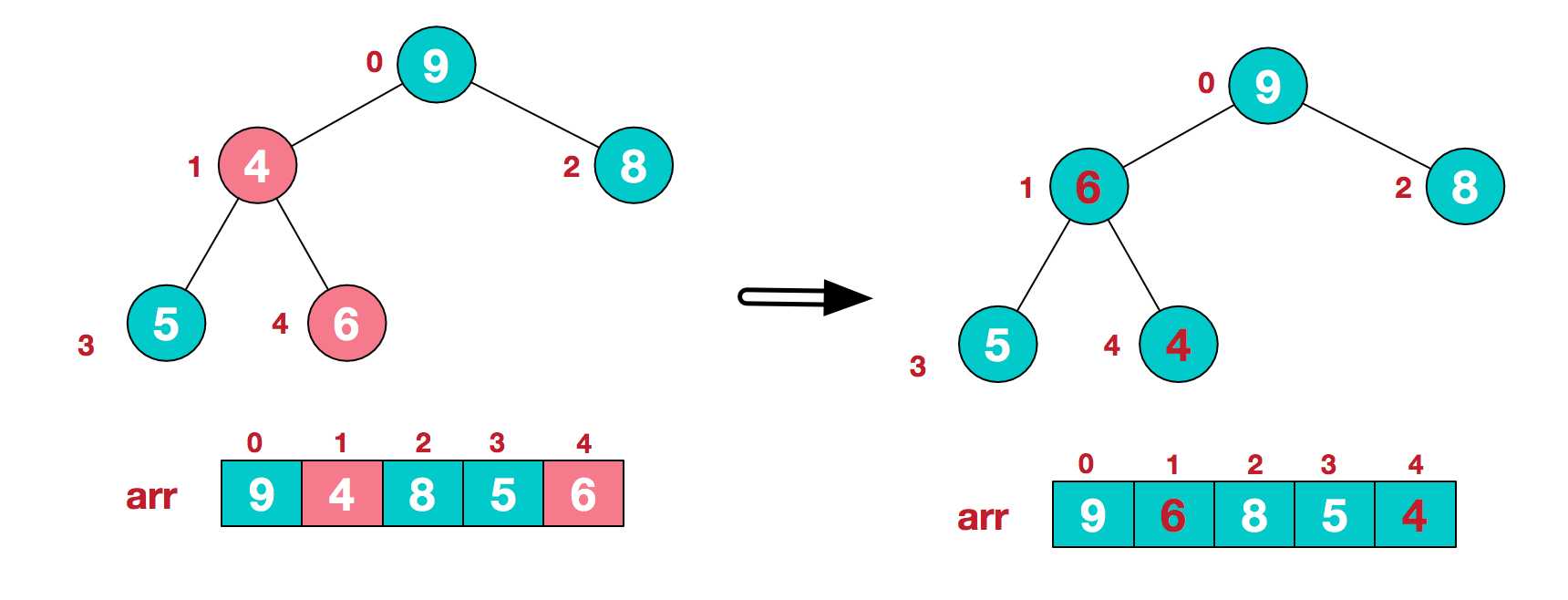
此时,我们就将一个无需序列构造成了一个大顶堆。
步骤二 将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换。
a.将堆顶元素9和末尾元素4进行交换
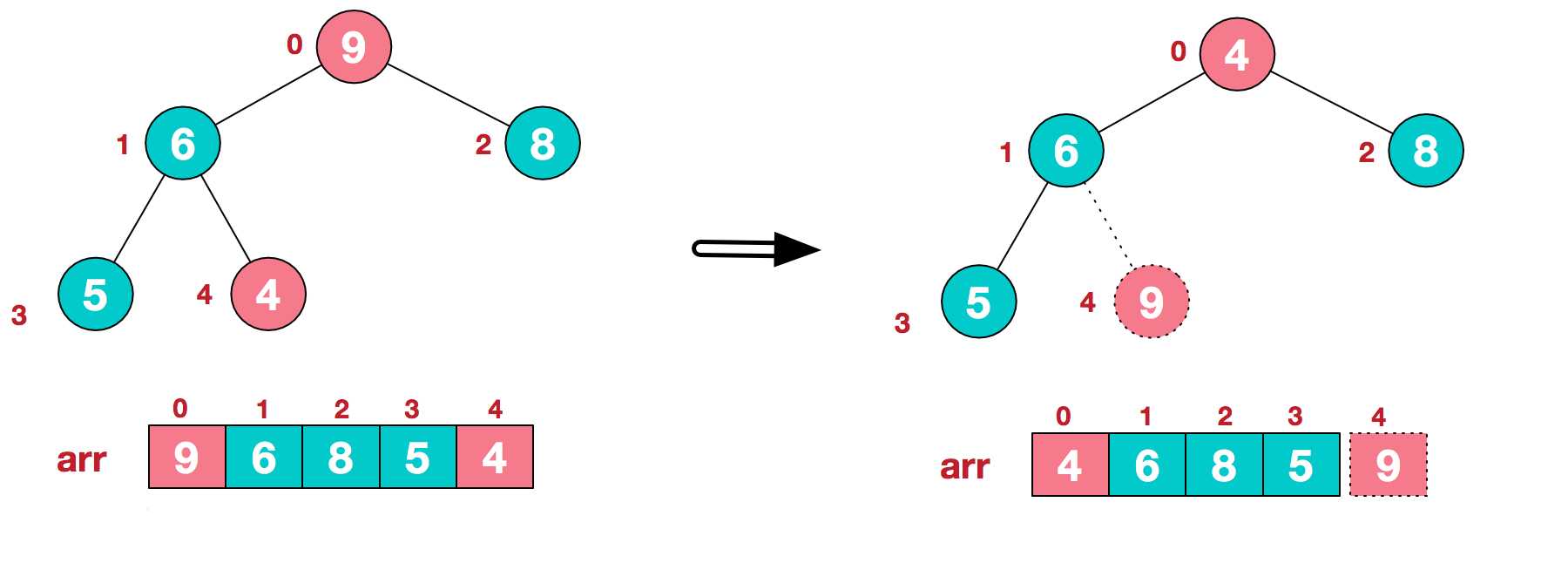
b.重新调整结构,使其继续满足堆定义
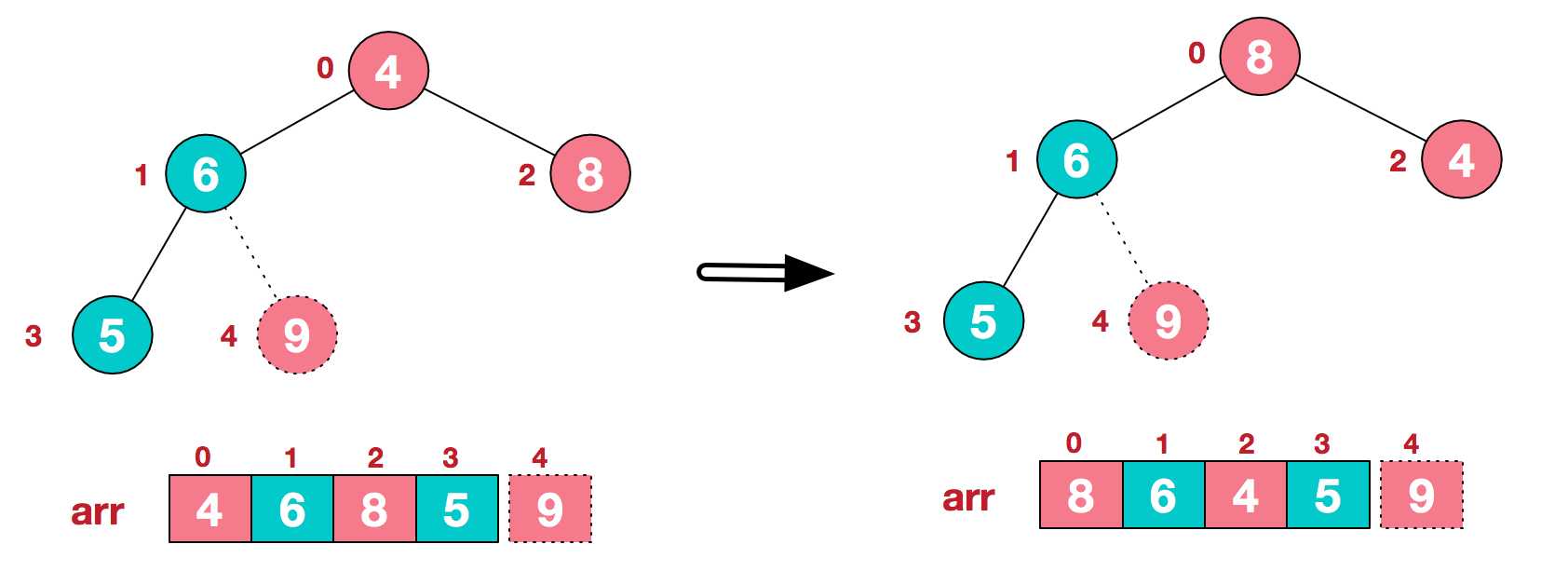
c.再将堆顶元素8与末尾元素5进行交换,得到第二大元素8.
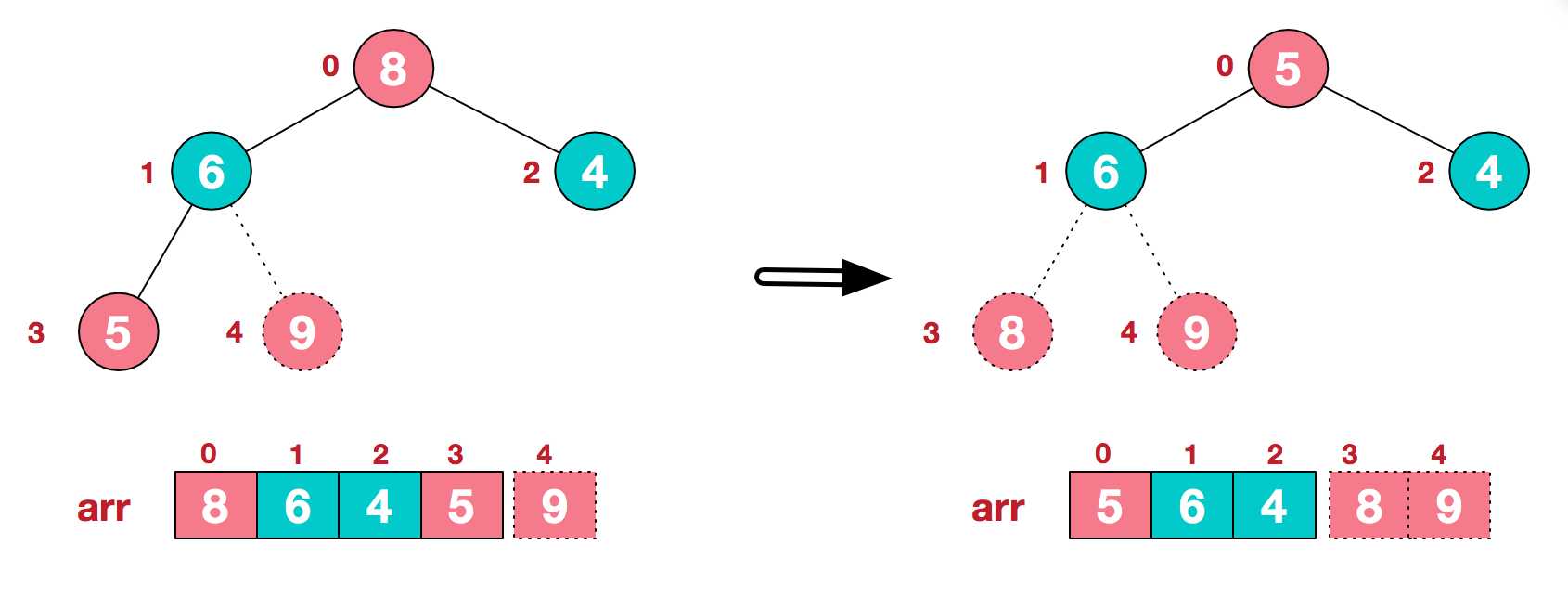
后续过程,继续进行调整,交换,如此反复进行,最终使得整个序列有序
再简单总结下堆排序的基本思路:
a.将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
b.将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
c.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
#include<iostream> #include<cstdio> #include<cmath> using namespace std; int n,m,a[10005],sum=0,ans=0; void put(int k) { sum++; //加入新元素,sum加一 int now,next; //now记录新元素的编号,next记录该元素的父亲的编号 a[sum]=k; now=sum; while(now>1) //如果now不是根结点 { next=now/2; if(a[now]>=a[next]) return ; //如果孩子大于等于父亲,说明符合小根堆的特征,直接返回 swap(a[now],a[next]); now=next; } } int get() //从最小堆中取出一个元素 { int now=1,next,small; //now是记录取出的元素在堆中的编号,根据题意我们要取得是最小值,根结点符合,所以now赋值为1 small=a[1]; //small记录堆中的最小元素 a[1]=a[sum]; //用堆中最后一个元素将第一个元素覆盖 sum--; //堆的长度减一 while(now*2<=sum) //now的左孩子要在堆内 { next=now*2; //next记录now的左孩子的编号 if(a[next]>a[next+1]&&next+1<=sum) next++; //如果now的右孩子next+1在堆内且右孩子小于左孩子,next加一改成右孩子的编号,保证next记录的元素是now孩子中最小的 if(a[now]<=a[next]) return small; //如果now比最小孩子还小,说明符合小根堆的特征,直接返回small swap(a[now],a[next]); //如果到了这一步,说明now比next大,那么就要交换它们两个的值 now=next; //now换成next的值继续往下搜 } return small; //这里别忘了再返回一次 } int main() { int x,y; cin>>n; for(int i=1;i<=n;i++) { cin>>m; put(m); //将输入的m入堆,并进行调整,维持它的最小堆 } for(int i=1;i<n;i++) { x=get(); //取出堆中的最小元素 y=get(); //取出堆中的次小元素 ans+=x+y; //记录消耗的体力值 put(x+y); //将新合成的果堆入堆 } cout<<ans<<endl; return 0; }
标签:数据结构 最大值 ble org 执行 最小堆 第一个 重建 图片
原文地址:https://www.cnblogs.com/xcg123/p/10776424.html