标签:char pac min getch sim 等于 pre 图片 \n
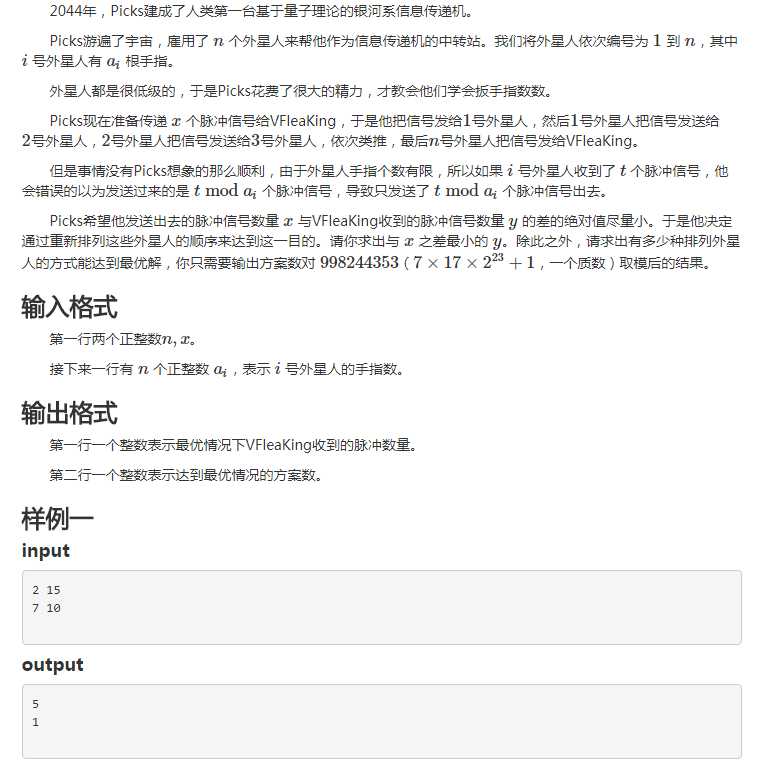
首先可以发现有效果的\(a_i\)大小一定是递减的,而且一定小于等于当前值
所以我们可以从大到小考虑每个\(a_i\),当确定了一个有效果的\(a_i\)时,\((a_i,x]\)的数都可以随意的放在\(a_i\)之后并且不会造成影响
设\(f_i\)表示考虑完所有的大小大于\(i\)数,当前数值为\(i\)的方案数
\(s_i\)表示\(\le i\)的数的个数
那么\(f_{i\%a[j]}=f_{i}\times A_{s_{i}-1-s[i\%a[j]]}^{s_i-1}\)
表示每次把\(i\%a[j]\sim i-1\)之间的数插在所有\(\le i\)之间的数的方案数
其实这个\(dp\)的过程就相当于把一个一个的数往数列里插入计算贡献,只不过这个\(dp\)的过程是反着的
#include<cstdio>
#include<cstring>
#include<algorithm>
const int M = 5005 ;
const int mod = 998244353 ;
using namespace std ;
inline int read() {
char c = getchar() ; int x = 0 , w = 1 ;
while(c>'9'||c<'0') { if(c=='-') w = -1 ; c = getchar() ; }
while(c>='0'&&c<='9') { x = x*10+c-'0' ; c = getchar() ; }
return x*w ;
}
int n , m , x , minv = 5000 ;
int sum[M] , val[M] , f[M] ;
int inv[M] , fac[M] , finv[M] ;
inline int A(int n , int m) {
return 1LL * fac[n] * finv[n - m] % mod ;
}
int main() {
n = read() ; x = read() ;
for(int i = 1 ; i <= n ; i ++) {
val[i] = read() ; minv = min( minv , val[i] ) ;
m = max(m , val[i]) ; ++ sum[val[i]] ;
}
for(int i = 1 ; i <= 5000 ; i ++) sum[i] += sum[i - 1] ;
inv[1] = 1 ; for(int i = 2 ; i <= 5000 ; i ++) inv[i] = 1LL * (mod - mod / i) * inv[mod % i] % mod ;
fac[0] = 1 ; for(int i = 1 ; i <= 5000 ; i ++) fac[i] = 1LL * fac[i - 1] * i % mod ;
finv[0] = 1 ; for(int i = 1 ; i <= 5000 ; i ++) finv[i] = 1LL * finv[i - 1] * inv[i] % mod ;
f[x] = 1LL * fac[n] * finv[sum[x]] % mod ;
for(int i = x ; i ; i --)
for(int j = 1 ; j <= n ; j ++)
if(val[j] <= i)
f[i % val[j]] = ( f[i % val[j]] + 1LL * f[i] * A( sum[i] - 1 , sum[i] - sum[i % val[j]] - 1 ) % mod ) % mod ;
for(int i = minv - 1 ; i >= 0 ; i --)
if(f[i]) {
printf("%d\n%d\n",i , f[i]) ;
break ;
}
return 0 ;
}标签:char pac min getch sim 等于 pre 图片 \n
原文地址:https://www.cnblogs.com/beretty/p/10777537.html