标签:target 节点 一个 维护 位置 lan 先序遍历 图片 等于
感谢weeping
dfs序是树在dfs先序遍历时的序列,将树形结构转化成序列问题处理。
dfs有一个很好的性质:一棵子树所在的位置处于一个连续区间中。
ps:deep[x]为x的深度,l[x]为dfs序中x的位置,r[x]为dfs序中x子树的结束位置
1.点修改,子树和查询
在dfs序中,子树处于一个连续区间中。所以这题可以转化为:点修改,区间查询。用树状数组或线段树即可。
2.树链修改,单点查询
将一条树链x,y上的所有点的权值加v。这个问题可以等价为:
1).x到根节点的链上所有节点权值加v。
2).y到根节点的链上所有节点权值加v。
3).lca(x,y)到根节点的链上所有节点权值和减v。
4).fa(lca(x,y))到根节点的链上所有节点权值和减v。
上面四个操作可以归结为:节点x到根节点链上所有节点的权值加减v。修改节点x权值,当且仅当y是x的祖先节点时,x对y的值有贡献。
所以节点y的权值可以转化为节点y的子树节点贡献和。从贡献和的角度想:这就是点修改,区间和查询问题。
修改树链x,y等价于add(l[x],v),add(l[y],v),add(l[lca(x,y)],-v),add(l[fa(lca(x,y))],-v)。
查询:get_sum(r[x])-get_sum(l[x]-1)
用树状数组或线段树即可。
3.树链修改,子树和查询
树链修改部分同上一问题。下面考虑子树和查询问题:前一问是从贡献的角度想,子树和同理。
对于节点y其到根节点的权值和,考虑其子节点x的贡献:w[x]*(deep[x]-deep[y]+1) = w[x]*(deep[x]+1)-w[x]*deep[y]
所以节点y的子树和为:
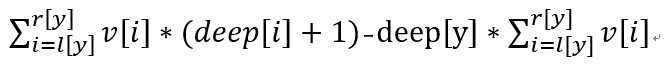
ps:公式中的v[i]为手误,应为w[i]。
所以用两个树状数组或线段树即可:
第一个维护∑w[i]*(deep[i]+1):支持操作单点修改,区间和查询。(这也就是问题2)
第二个维护∑ w[i]:支持操作单点修改,区间查询。(这其实也是问题2)
4.单点更新,树链和查询
树链和查询与树链修改类似,树链和(x,y)等于下面四个部分和相加:
1).x到根节点的链上所有节点权值加。
2).y到根节点的链上所有节点权值加。
3).lca(x,y)到根节点的链上所有节点权值和的-1倍。
4).fa(lca(x,y))到根节点的链上所有节点权值和的-1倍。
所以问题转化为:查询点x到根节点的链上的所有节点权值和。
修改节点x权值,当且仅当y是x的子孙节点时,x对y的值有贡献。
差分前缀和,y的权值等于dfs中[1,l[y]]的区间和。
单点修改:add(l[x],v),add(r[x]+1,-v);
5.子树修改,单点查询
修改节点x的子树权值,在dfs序上就是区间修改,单点权值查询就是单点查询。
区间修改,单点查询问题:树状数组或线段树即可;
6.子树修改,子树和查询
题目等价与区间修改,区间查询问题。用树状数组或线段树即可。
7.子树修改,树链查询
树链查询同上,等价为根节点到y节点的链上所有节点和问题。
修改节点x的子树权值,当且仅当y是x的子孙节点时(或y等于x),x对y的值有贡献。
x对根节点到y节点的链上所有节点和的贡献为:w[x]*(deep[y]-deep[x]+1)=w[x]*deep[y]-w[x]*(1-deep[x])
同问题三,用两个树状数组或线段树即可。
标签:target 节点 一个 维护 位置 lan 先序遍历 图片 等于
原文地址:https://www.cnblogs.com/a-blog-of-taojiayi-2003/p/10777334.html