数据结构6.2_二叉树

标签：span   https   alt   details   code   定义   info   blank   存在   

1、二叉树的定义：

二叉树（Binary True）是另一种树型结构，它的特点是每个结点至多只有两棵子树（即二叉树中不存在度大于2的结点），并且，二叉树的子树有左右之分，其次序不能任意颠倒。

以下是二叉树的五种基本形态：

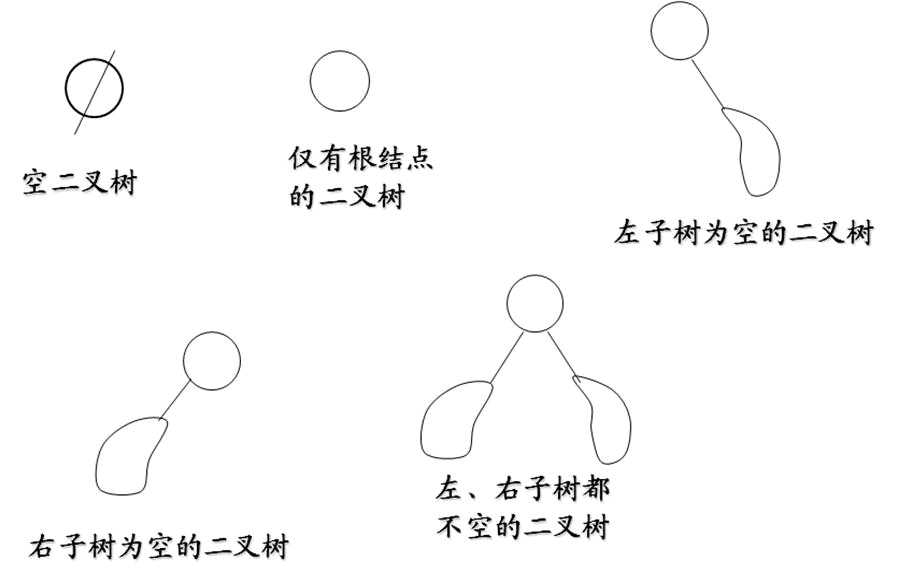
2、二叉树的性质：

二叉树的结构特点和性质：https://blog.csdn.net/qq_34322188/article/details/82346068

二叉树的性质有三条：

1）性质1：在二叉树的第i层上至多有2^(i-1)个结点（i>=1）；  //利用归纳法可以证明

2）性质2：深度为k的二叉树至多有2^k - 1个结点（k >= 1）； //可以利用性质1证明

3）性质3：对于任何二叉树T，如果其终端结点的个数为n0，度为2的结点树为n2，则n0=n2+1； //可以从二叉树的分支数量B=n1+n2，n1是度为1的结点；所有结点的度不超过2，n=n0+n1+n2；去证明；

完全二叉树 和 满二叉树 是两种形态特殊的二叉树。

浅谈数据结构-二叉树：https://www.cnblogs.com/polly333/p/4740355.html

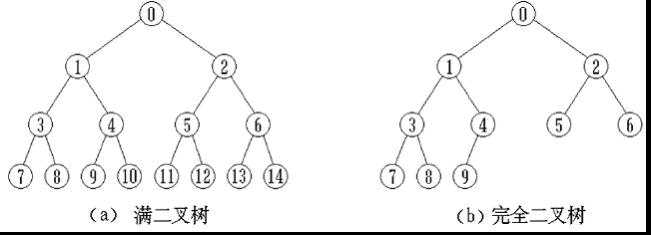
通过观察上图可以发现，完全二叉树的所有编号与结点可以与满二叉树的编号一一对应。

完全二叉树的特点是：

1）叶子结点只可能在层次最大的两层出现；

2）对任一结点，若其右分支下的子孙的最大层次为l，则其左分支下的子孙的最大层次必为l或l+1；

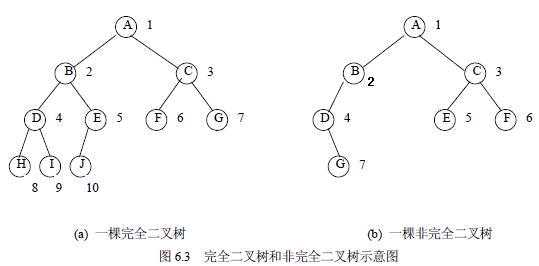
完全二叉树将在很多场合下出现，下面将介绍完全二叉树的两个重要特性：

1）特性1：

2）特性2：

3、二叉树的存储结构：

数据结构6.2_二叉树

标签：span   https   alt   details   code   定义   info   blank   存在   

原文地址：https://www.cnblogs.com/grooovvve/p/10779280.html