数据竞赛实战（3）——公共自行车使用量预测

时间：2019-04-29 21:10:06 阅读：144 评论：0 收藏：0 [点我收藏+]

标签：count des idt sel 网格删除 6.2 mem 9.1

前言

1，背景介绍

　　公共自行车低碳，环保，健康，并且解决了交通中“最后一公里”的痛点，在全国各个城市越来越受欢迎。本次练习的数据取自于两个城市某街道上的几处公共自行车停车桩。我们希望根据时间，天气等信息，预测出该街区在一小时内的被借取的公共自行车的数量。

2，任务类型

　　回归

3，数据文件说明

train.csv 　　　　　　训练集　　文件大小为273KB

test.csv 　　　　预测集　　文件大小为179KB

sample_submit.csv 　提交示例文件大小为97KB

4，数据变量说明　

　　训练集中共有10000条样本，预测集中有7000条样本　

技术图片

5，评估方法

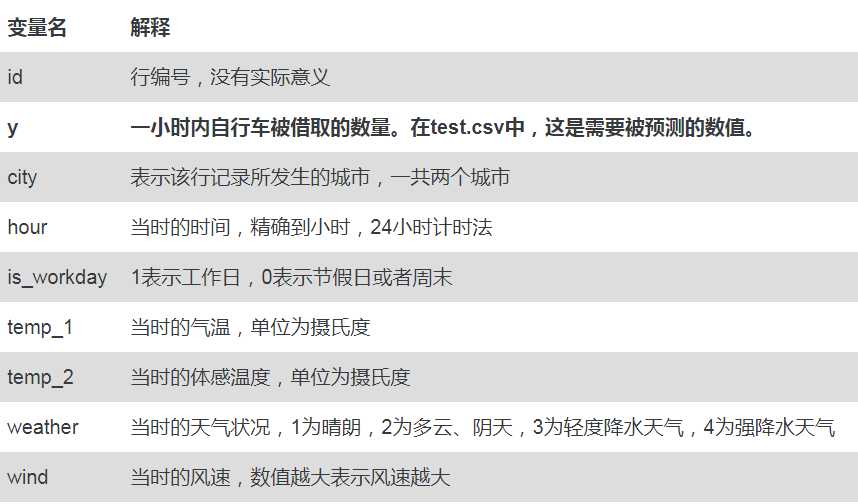
　　评价方法为RMSE（Root of Mean Squared Error）

技术图片

6，完整代码，请移步小编的GitHub

　　传送门：请点击我

数据预处理

1，观察数据有没有缺失值

print(train.info())


<class ‘pandas.core.frame.DataFrame‘>
RangeIndex: 10000 entries, 0 to 9999
Data columns (total 7 columns):
city          10000 non-null int64
hour          10000 non-null int64
is_workday    10000 non-null int64
weather       10000 non-null int64
temp_1        10000 non-null float64
temp_2        10000 non-null float64
wind          10000 non-null int64
dtypes: float64(2), int64(5)
memory usage: 547.0 KB
None

　　我们可以看到，共有10000个观测值，没有缺失值。

2，观察每个变量的基础描述信息

print(train.describe())


               city          hour      ...             temp_2          wind
count  10000.000000  10000.000000      ...       10000.000000  10000.000000
mean       0.499800     11.527500      ...          15.321230      1.248600
std        0.500025      6.909777      ...          11.308986      1.095773
min        0.000000      0.000000      ...         -15.600000      0.000000
25%        0.000000      6.000000      ...           5.800000      0.000000
50%        0.000000     12.000000      ...          16.000000      1.000000
75%        1.000000     18.000000      ...          24.800000      2.000000
max        1.000000     23.000000      ...          46.800000      7.000000

[8 rows x 7 columns]

　　通过观察可以得出一些猜测，如城市0 和城市1基本可以排除南方城市；整个观测记录时间跨度较长，还可能包含了一个长假期数据等等。

3，查看相关系数

　　（为了方便查看，绝对值低于0.2的就用nan替代）

    corr = feature_data.corr()
    corr[np.abs(corr) < 0.2] = np.nan
    print(corr)


            city  hour  is_workday  weather    temp_1    temp_2  wind
city         1.0   NaN         NaN      NaN       NaN       NaN   NaN
hour         NaN   1.0         NaN      NaN       NaN       NaN   NaN
is_workday   NaN   NaN         1.0      NaN       NaN       NaN   NaN
weather      NaN   NaN         NaN      1.0       NaN       NaN   NaN
temp_1       NaN   NaN         NaN      NaN  1.000000  0.987357   NaN
temp_2       NaN   NaN         NaN      NaN  0.987357  1.000000   NaN
wind         NaN   NaN         NaN      NaN       NaN       NaN   1.0

　　从相关性角度来看，用车的时间和当时的气温对借取数量y有较强的关系；气温和体感气温显强正相关（共线性），这个和常识一致。

模型训练及其结果展示

1，标杆模型：简单线性回归模型

　　该模型预测结果的RMSE为：39.132

# -*- coding: utf-8 -*-

# 引入模块
from sklearn.linear_model import LinearRegression
import pandas as pd

# 读取数据
train = pd.read_csv("train.csv")
test = pd.read_csv("test.csv")
submit = pd.read_csv("sample_submit.csv")

# 删除id
train.drop(‘id‘, axis=1, inplace=True)
test.drop(‘id‘, axis=1, inplace=True)

# 取出训练集的y
y_train = train.pop(‘y‘)

# 建立线性回归模型
reg = LinearRegression()
reg.fit(train, y_train)
y_pred = reg.predict(test)

# 若预测值是负数，则取0
y_pred = map(lambda x: x if x >= 0 else 0, y_pred)

# 输出预测结果至my_LR_prediction.csv
submit[‘y‘] = y_pred
submit.to_csv(‘my_LR_prediction.csv‘, index=False)

2，决策树回归模型

　　该模型预测结果的RMSE为：28.818

# -*- coding: utf-8 -*-

# 引入模块
from sklearn.tree import DecisionTreeRegressor
import pandas as pd

# 读取数据
train = pd.read_csv("train.csv")
test = pd.read_csv("test.csv")
submit = pd.read_csv("sample_submit.csv")

# 删除id
train.drop(‘id‘, axis=1, inplace=True)
test.drop(‘id‘, axis=1, inplace=True)

# 取出训练集的y
y_train = train.pop(‘y‘)

# 建立最大深度为5的决策树回归模型
reg = DecisionTreeRegressor(max_depth=5)
reg.fit(train, y_train)
y_pred = reg.predict(test)

# 输出预测结果至my_DT_prediction.csv
submit[‘y‘] = y_pred
submit.to_csv(‘my_DT_prediction.csv‘, index=False)

3，Xgboost回归模型

　　该模型预测结果的RMSE为：18.947

# -*- coding: utf-8 -*-

# 引入模块
from xgboost import XGBRegressor
import pandas as pd

# 读取数据
train = pd.read_csv("train.csv")
test = pd.read_csv("test.csv")
submit = pd.read_csv("sample_submit.csv")

# 删除id
train.drop(‘id‘, axis=1, inplace=True)
test.drop(‘id‘, axis=1, inplace=True)

# 取出训练集的y
y_train = train.pop(‘y‘)

# 建立一个默认的xgboost回归模型
reg = XGBRegressor()
reg.fit(train, y_train)
y_pred = reg.predict(test)

# 输出预测结果至my_XGB_prediction.csv
submit[‘y‘] = y_pred
submit.to_csv(‘my_XGB_prediction.csv‘, index=False)

4，Xgboost回归模型调参过程

　　Xgboost的相关博客：请点击我

　　参数调优的方法步骤一般情况如下：

1，选择较高的学习速率（learning rate）。一般情况下，学习速率的值为0.1。但是对于不同的问题，理想的学习速率有时候会在0.05到0.3之间波动。选择对应于此学习速率的理想决策树数量。 Xgboost有一个很有用的函数“cv”，这个函数可以在每一次迭代中使用交叉验证，并返回理想的决策树数量。
2，对于给定的学习速率和决策树数量，进行决策树特定参数调优（max_depth，min_child_weight，gamma，subsample，colsample_bytree）。在确定一棵树的过程中，我们可以选择不同的参数。
3，Xgboost的正则化参数的调优。（lambda，alpha）。这些参数可以降低模型的复杂度，从而提高模型的表现。
4，降低学习速率，确定理想参数。

5，Xgboost使用GridSearchCV调参过程

5.1，Xgboost 的默认参数如下（在sklearn库中的默认参数）：

def __init__(self, max_depth=3, learning_rate=0.1, n_estimators=100,
                 silent=True, objective="rank:pairwise", booster=‘gbtree‘,
                 n_jobs=-1, nthread=None, gamma=0, min_child_weight=1, max_delta_step=0,
                 subsample=1, colsample_bytree=1, colsample_bylevel=1,
                 reg_alpha=0, reg_lambda=1, scale_pos_weight=1,
                 base_score=0.5, random_state=0, seed=None, missing=None, **kwargs):

5.2，首先调n_estimators

def xgboost_parameter_tuning(feature_data, label_data, test_feature, submitfile):
    import xgboost as xgb
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error
    from sklearn.model_selection import GridSearchCV

    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)
    param_test1 = {
        ‘n_estimators‘: range(100, 1000, 100)
    }
    gsearch1 = GridSearchCV(estimator= xgb.XGBRegressor(
        learning_rate=0.1, max_depth=5,
        min_child_weight=1, gamma=0, subsample=0.8, colsample_bytree=0.8,
        nthread=4, scale_pos_weight=1, seed=27),
        param_grid=param_test1, iid=False, cv=5
    )


    gsearch1.fit(X_train, y_train)
    return gsearch1.best_params_, gsearch1.best_score_

　　得到结果如下（所以我们选择树的个数为200）：

{‘n_estimators‘: 200}
0.9013685759002941

5.3，调参 max_depth和min_child_weight

　　（树的最大深度，缺省值为3，范围是[1, 正无穷），树的深度越大，则对数据的拟合程度越高，但是通常取值为3-10）

　　（孩子节点中的最小的样本权重和，如果一个叶子节点的样本权重和小于min_child_weight则拆分过程结果）

　　下面我们对这两个参数调优，是因为他们对最终结果由很大的影响，所以我直接小范围微调。

def xgboost_parameter_tuning2(feature_data, label_data, test_feature, submitfile):
    import xgboost as xgb
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error
    from sklearn.model_selection import GridSearchCV

    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)

    param_test2 = {
        ‘max_depth‘: range(3, 10, 1),
        ‘min_child_weight‘: range(1, 6, 1),
    }
    gsearch1 = GridSearchCV(estimator= xgb.XGBRegressor(
        learning_rate=0.1, n_estimators=200
    ), param_grid=param_test2, cv=5)


    gsearch1.fit(X_train, y_train)
    return gsearch1.best_params_, gsearch1.best_score_

　　得到的结果如下：

{‘max_depth‘: 5, ‘min_child_weight‘: 5}
0.9030852081699604

　　我们对于数值进行较大跨度的48种不同的排列组合，可以看出理想的max_depth值为5，理想的min_child_weight值为5。

5.4，gamma参数调优

　　（gamma值使得算法更加conservation，且其值依赖于loss function，在模型中应该调参）

　　在已经调整好其他参数的基础上，我们可以进行gamma参数的调优了。Gamma参数取值范围可以很大，我这里把取值范围设置为5，其实我们也可以取更精确的gamma值。

def xgboost_parameter_tuning3(feature_data, label_data, test_feature, submitfile):
    import xgboost as xgb
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error
    from sklearn.model_selection import GridSearchCV

    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)

    param_test3 = {
        ‘gamma‘: [i/10.0 for i in range(0, 5)]
    }
    gsearch1 = GridSearchCV(estimator=xgb.XGBRegressor(
        learning_rate=0.1, n_estimators=200, max_depth=5, min_child_weight=5
    ), param_grid=param_test3, cv=5)


    gsearch1.fit(X_train, y_train)
    return gsearch1.best_params_, gsearch1.best_score_

结果如下：

{‘gamma‘: 0.0}
0.9024876500236406

5.5，调整subsample 和 colsample_bytree 参数

　　（subsample 用于训练模型的子样本占整个样本集合的比例，如果设置0.5则意味着XGBoost将随机的从整个样本集合中抽取出百分之50的子样本建立模型，这样能防止过拟合，取值范围为(0, 1]）

　　（在建立树的时候对特征采样的比例，缺省值为1，物质范围为(0, 1]）

　　下一步是尝试不同的subsample 和colsample_bytree 参数。我们分两个阶段来进行这个步骤。这两个步骤都取0.6,0.7,0.8,0.9 作为起始值。

def xgboost_parameter_tuning4(feature_data, label_data, test_feature, submitfile):
    import xgboost as xgb
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error
    from sklearn.model_selection import GridSearchCV

    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)

    param_test4 = {
        ‘subsample‘: [i / 10.0 for i in range(6, 10)],
        ‘colsample_bytree‘: [i / 10.0 for i in range(6, 10)]
    }
    gsearch1 = GridSearchCV(estimator=xgb.XGBRegressor(
        learning_rate=0.1, n_estimators=200, max_depth=5, min_child_weight=5， gamma=0
    ), param_grid=param_test4, cv=5)


    gsearch1.fit(X_train, y_train)
    return gsearch1.best_params_, gsearch1.best_score_

　　结果如下：

{‘colsample_bytree‘: 0.9, ‘subsample‘: 0.8}
0.9039011907271065

5.6，正则化参数调优

　　由于gamma函数提供了一种更加有效的降低过拟合的方法，大部分人很少会用到这个参数，但是我们可以尝试用一下这个参数。

def xgboost_parameter_tuning5(feature_data, label_data, test_feature, submitfile):
    import xgboost as xgb
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error
    from sklearn.model_selection import GridSearchCV

    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)

    param_test5 = {
        ‘reg_alpha‘: [0, 0.001, 0.005, 0.01, 0.05]
    }
    gsearch1 = GridSearchCV(estimator=xgb.XGBRegressor(
        learning_rate=0.1, n_estimators=200, max_depth=5, min_child_weight=5, gamma=0.0,
        colsample_bytree=0.9, subsample=0.8), param_grid=param_test5, cv=5)


    gsearch1.fit(X_train, y_train)
    return gsearch1.best_params_, gsearch1.best_score_

　　结果如下：

{‘reg_alpha‘: 0.01}
0.899800819611995

5.6，汇总出我们搜索到的最佳参数，然后训练

　　代码如下：

def xgboost_train(feature_data, label_data, test_feature, submitfile):
    import xgboost as xgb
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error

    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)
    params = {
        ‘learning_rate‘: 0.1,
        ‘n_estimators‘: 200,
        ‘max_depth‘: 5,
        ‘min_child_weight‘: 5,
        ‘gamma‘: 0.0,
        ‘colsample_bytree‘: 0.9,
        ‘subsample‘: 0.8,
        ‘reg_alpha‘: 0.01,

    }
    model = xgb.XGBRegressor(**params)
    model.fit(X_train, y_train)
    # 对测试集进行预测
    y_pred = model.predict(X_test)
    # 计算准确率
    MSE = mean_squared_error(y_test, y_pred)
    RMSE = np.sqrt(MSE)
    print(RMSE)

    submit = pd.read_csv(submitfile)
    submit[‘y‘] = model.predict(test_feature)
    submit.to_csv(‘my_xgboost_prediction1.csv‘, index=False)

　　我们可以对比上面的结果，最终的结果为15.208，比直接使用xgboost提高了3.92.

最终所有代码总结如下：

#_*_coding:utf-8_*_
import numpy as np
import pandas as pd


def load_data(trainfile, testfile):
    traindata = pd.read_csv(trainfile)
    testdata = pd.read_csv(testfile)
    print(traindata.shape)   #(10000, 9)
    print(testdata.shape)    #(7000, 8)
    # print(traindata)
    print(type(traindata))
    feature_data = traindata.iloc[:, 1:-1]
    label_data = traindata.iloc[:, -1]
    test_feature = testdata.iloc[:, 1:]
    return feature_data, label_data, test_feature

def xgboost_train(feature_data, label_data, test_feature, submitfile):
    import xgboost as xgb
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error

    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)
    params = {
        ‘learning_rate‘: 0.1,
        ‘n_estimators‘: 200,
        ‘max_depth‘: 5,
        ‘min_child_weight‘: 5,
        ‘gamma‘: 0.0,
        ‘colsample_bytree‘: 0.9,
        ‘subsample‘: 0.8,
        ‘reg_alpha‘: 0.01,

    }
    model = xgb.XGBRegressor()
    model.fit(X_train, y_train)
    # 对测试集进行预测
    y_pred = model.predict(X_test)
    # 计算准确率
    MSE = mean_squared_error(y_test, y_pred)
    RMSE = np.sqrt(MSE)
    print(RMSE)

    submit = pd.read_csv(submitfile)
    submit[‘y‘] = model.predict(test_feature)
    submit.to_csv(‘my_xgboost_prediction.csv‘, index=False)


def xgboost_parameter_tuning1(feature_data, label_data, test_feature, submitfile):
    import xgboost as xgb
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error
    from sklearn.model_selection import GridSearchCV

    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)

    param_test1 = {
        ‘n_estimators‘: range(100, 1000, 100)
    }
    gsearch1 = GridSearchCV(estimator= xgb.XGBRegressor(
        learning_rate=0.1, max_depth=5,
        min_child_weight=1, gamma=0, subsample=0.8, colsample_bytree=0.8,
        nthread=4, scale_pos_weight=1, seed=27),
        param_grid=param_test1, iid=False, cv=5
    )


    gsearch1.fit(X_train, y_train)
    return gsearch1.best_params_, gsearch1.best_score_

def xgboost_parameter_tuning2(feature_data, label_data, test_feature, submitfile):
    import xgboost as xgb
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error
    from sklearn.model_selection import GridSearchCV

    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)

    param_test2 = {
        ‘max_depth‘: range(3, 10, 1),
        ‘min_child_weight‘: range(1, 6, 1),
    }
    gsearch1 = GridSearchCV(estimator= xgb.XGBRegressor(
        learning_rate=0.1, n_estimators=200
    ), param_grid=param_test2, cv=5)


    gsearch1.fit(X_train, y_train)
    return gsearch1.best_params_, gsearch1.best_score_

def xgboost_parameter_tuning3(feature_data, label_data, test_feature, submitfile):
    import xgboost as xgb
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error
    from sklearn.model_selection import GridSearchCV

    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)

    param_test3 = {
        ‘gamma‘: [i/10.0 for i in range(0, 5)]
    }
    gsearch1 = GridSearchCV(estimator=xgb.XGBRegressor(
        learning_rate=0.1, n_estimators=200, max_depth=5, min_child_weight=5
    ), param_grid=param_test3, cv=5)


    gsearch1.fit(X_train, y_train)
    return gsearch1.best_params_, gsearch1.best_score_

def xgboost_parameter_tuning4(feature_data, label_data, test_feature, submitfile):
    import xgboost as xgb
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error
    from sklearn.model_selection import GridSearchCV

    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)

    param_test4 = {
        ‘subsample‘: [i / 10.0 for i in range(6, 10)],
        ‘colsample_bytree‘: [i / 10.0 for i in range(6, 10)]
    }
    gsearch1 = GridSearchCV(estimator=xgb.XGBRegressor(
        learning_rate=0.1, n_estimators=200, max_depth=5, min_child_weight=5,gamma=0.0
    ), param_grid=param_test4, cv=5)


    gsearch1.fit(X_train, y_train)
    return gsearch1.best_params_, gsearch1.best_score_

def xgboost_parameter_tuning5(feature_data, label_data, test_feature, submitfile):
    import xgboost as xgb
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error
    from sklearn.model_selection import GridSearchCV

    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)

    param_test5 = {
        ‘reg_alpha‘: [0, 0.001, 0.005, 0.01, 0.05]
    }
    gsearch1 = GridSearchCV(estimator=xgb.XGBRegressor(
        learning_rate=0.1, n_estimators=200, max_depth=5, min_child_weight=5, gamma=0.0,
        colsample_bytree=0.9, subsample=0.8), param_grid=param_test5, cv=5)


    gsearch1.fit(X_train, y_train)
    return gsearch1.best_params_, gsearch1.best_score_

if __name__ == ‘__main__‘:
    trainfile = ‘data/train.csv‘
    testfile = ‘data/test.csv‘
    submitfile = ‘data/sample_submit.csv‘
    feature_data, label_data, test_feature = load_data(trainfile, testfile)
    xgboost_train(feature_data, label_data, test_feature, submitfile)

6，随机森林回归模型　

　　该模型预测结果的RMSE为：18.947

#_*_coding:utf-8_*_
import numpy as np
import pandas as pd


def load_data(trainfile, testfile):
    traindata = pd.read_csv(trainfile)
    testdata = pd.read_csv(testfile)
    feature_data = traindata.iloc[:, 1:-1]
    label_data = traindata.iloc[:, -1]
    test_feature = testdata.iloc[:, 1:]
    return feature_data, label_data, test_feature

def random_forest_train(feature_data, label_data, test_feature, submitfile):
    from sklearn.ensemble import RandomForestRegressor
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error

    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)

    model = RandomForestRegressor()
    model.fit(X_train, y_train)
    # 对测试集进行预测
    y_pred = model.predict(X_test)
    # 计算准确率
    MSE = mean_squared_error(y_test, y_pred)
    RMSE = np.sqrt(MSE)
    print(RMSE)

    submit = pd.read_csv(submitfile)
    submit[‘y‘] = model.predict(test_feature)
    submit.to_csv(‘my_random_forest_prediction.csv‘, index=False)


if __name__ == ‘__main__‘:
    trainfile = ‘data/train.csv‘
    testfile = ‘data/test.csv‘
    submitfile = ‘data/sample_submit.csv‘
    feature_data, label_data, test_feature = load_data(trainfile, testfile)
    random_forest_train(feature_data, label_data, test_feature, submitfile)

　　技术图片

7，随机森林回归模型调参过程

　　随机森林的相关博客：请点击我

　　首先，我们看一下随机森林的调参过程

技术图片

1，首先先调即不会增加模型复杂度，又对模型影响最大的参数n_estimators（学习曲线）
2，找到最佳值后，调max_depth（单个网格搜索，也可以使用学习曲线）
　　（一般根据数据的大小来进行一个探视，当数据集很小的时候，可以采用1~10，或者1~20这样的试探，但是对于大型数据来说骂我们应该尝试30~50层深度（或许更深））
3，接下来依次对各个参数进行调参
　　（注意，对于大型数据集，max_leaf_nodes可以尝试从1000来构建，先输入1000，每100个叶子一个区间，再逐渐缩小范围；对于min_samples_split和min_samples_leaf，一般从他们的最小值开始向上增加10 或者20，面对高维度高样本数据，如果不放心可以直接50+，对于大型数据可能需要200~300的范围，如果调整的时候发现准确率无论如何都上不来，可以大胆放心的调试一个很大的数据，大力限制模型的复杂度。）

7.1 使用gridsearchcv探索n_estimators的最佳值

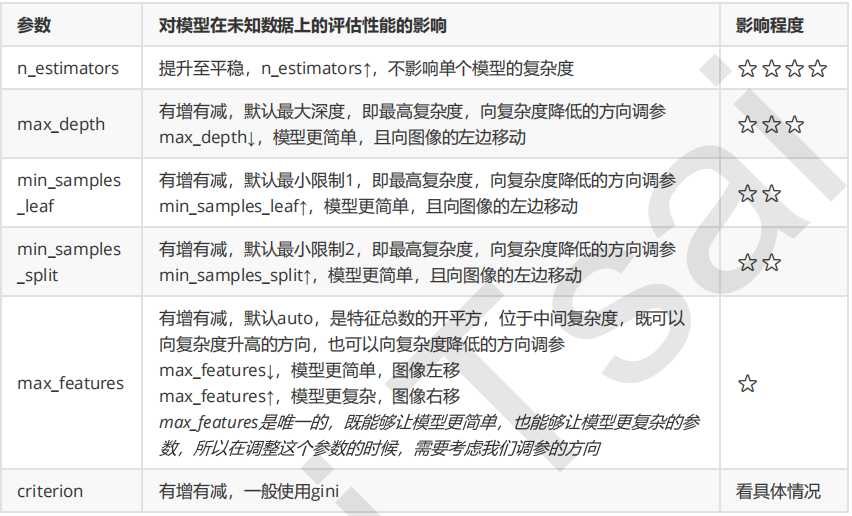
def random_forest_parameter_tuning1(feature_data, label_data, test_feature):
    from sklearn.ensemble import RandomForestRegressor
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error
    from sklearn.model_selection import GridSearchCV

    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)
    param_test1 = {
        ‘n_estimators‘: range(10, 71, 10)
    }
    model = GridSearchCV(estimator=RandomForestRegressor(
        min_samples_split=100, min_samples_leaf=20, max_depth=8, max_features=‘sqrt‘,
        random_state=10), param_grid=param_test1, cv=5
    )
    model.fit(X_train, y_train)
    # 对测试集进行预测
    y_pred = model.predict(X_test)
    # 计算准确率
    MSE = mean_squared_error(y_test, y_pred)
    RMSE = np.sqrt(MSE)
    print(RMSE)
    return model.best_score_, model.best_params_

　　结果如下：

{‘n_estimators‘: 70}
0.6573670183811001

　　这样我们得到了最佳的弱学习器迭代次数，为70.。

7.2 对决策树最大深度 max_depth 和内部节点再划分所需要的最小样本数求最佳值

　　我们首先得到了最佳弱学习器迭代次数，接着我们对决策树最大深度max_depth和内部节点再划分所需要最小样本数min_samples_split进行网格搜索。

def random_forest_parameter_tuning2(feature_data, label_data, test_feature):
    from sklearn.ensemble import RandomForestRegressor
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error
    from sklearn.model_selection import GridSearchCV

    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)
    param_test2 = {
        ‘max_depth‘: range(3, 14, 2),
        ‘min_samples_split‘: range(50, 201, 20)
    }
    model = GridSearchCV(estimator=RandomForestRegressor(
        n_estimators=70, min_samples_leaf=20, max_features=‘sqrt‘, oob_score=True,
        random_state=10), param_grid=param_test2, cv=5
    )
    model.fit(X_train, y_train)
    # 对测试集进行预测
    y_pred = model.predict(X_test)
    # 计算准确率
    MSE = mean_squared_error(y_test, y_pred)
    RMSE = np.sqrt(MSE)
    print(RMSE)
    return model.best_score_, model.best_params_

　　结果为：

{‘max_depth‘: 13, ‘min_samples_split‘: 50}
0.7107311632187736

　　对于内部节点再划分所需要最小样本数min_samples_split，我们暂时不能一起定下来，因为这个还和决策树其他的参数存在关联。

7.3 求内部节点再划分所需要的最小样本数min_samples_split和叶子节点最小样本数min_samples_leaf的最佳参数

　　下面我们对内部节点在划分所需要最小样本数min_samples_split和叶子节点最小样本数min_samples_leaf一起调参。

def random_forest_parameter_tuning3(feature_data, label_data, test_feature):
    from sklearn.ensemble import RandomForestRegressor
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error
    from sklearn.model_selection import GridSearchCV

    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)
    param_test3 = {
        ‘min_samples_split‘: range(10, 90, 20),
        ‘min_samples_leaf‘: range(10, 60, 10),
    }
    model = GridSearchCV(estimator=RandomForestRegressor(
        n_estimators=70, max_depth=13, max_features=‘sqrt‘, oob_score=True,
        random_state=10), param_grid=param_test3, cv=5
    )
    model.fit(X_train, y_train)
    # 对测试集进行预测
    y_pred = model.predict(X_test)
    # 计算准确率
    MSE = mean_squared_error(y_test, y_pred)
    RMSE = np.sqrt(MSE)
    print(RMSE)
    return model.best_score_, model.best_params_

　　结果如下：

{‘min_samples_leaf‘: 10, ‘min_samples_split‘: 10}
0.7648492269870218

7.4 求最大特征数max_features的最佳参数

def random_forest_parameter_tuning4(feature_data, label_data, test_feature):
    from sklearn.ensemble import RandomForestRegressor
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error
    from sklearn.model_selection import GridSearchCV

    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)
    param_test3 = {
        ‘max_features‘: range(3, 9, 2),
    }
    model = GridSearchCV(estimator=RandomForestRegressor(
        n_estimators=70, max_depth=13, min_samples_split=10, min_samples_leaf=10, oob_score=True,
        random_state=10), param_grid=param_test3, cv=5
    )
    model.fit(X_train, y_train)
    # 对测试集进行预测
    y_pred = model.predict(X_test)
    # 计算准确率
    MSE = mean_squared_error(y_test, y_pred)
    RMSE = np.sqrt(MSE)
    print(RMSE)
    return model.best_score_, model.best_params_

　　结果如下：

{‘max_features‘: 7}
0.881211719251515

7.5 汇总出我们搜索到的最佳参数，然后训练

def random_forest_train(feature_data, label_data, test_feature, submitfile):
    from sklearn.ensemble import RandomForestRegressor
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error

    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)
    params = {
        ‘n_estimators‘: 70,
        ‘max_depth‘: 13,
        ‘min_samples_split‘: 10,
        ‘min_samples_leaf‘: 10,
        ‘max_features‘: 7
    }
    model = RandomForestRegressor(**params)
    model.fit(X_train, y_train)
    # 对测试集进行预测
    y_pred = model.predict(X_test)
    # 计算准确率
    MSE = mean_squared_error(y_test, y_pred)
    RMSE = np.sqrt(MSE)
    print(RMSE)

    submit = pd.read_csv(submitfile)
    submit[‘y‘] = model.predict(test_feature)
    submit.to_csv(‘my_random_forest_prediction1.csv‘, index=False)

　　最终计算得到的结果如下：技术图片

　　我们发现，经过调参，结果由17.144 优化到16.251，效果相对Xgboost来说，不是很大。所以最终我们选择Xgboost算法。

7.6 所有代码如下：

#_*_coding:utf-8_*_
import numpy as np
import pandas as pd


def load_data(trainfile, testfile):
    traindata = pd.read_csv(trainfile)
    testdata = pd.read_csv(testfile)
    feature_data = traindata.iloc[:, 1:-1]
    label_data = traindata.iloc[:, -1]
    test_feature = testdata.iloc[:, 1:]
    return feature_data, label_data, test_feature

def random_forest_train(feature_data, label_data, test_feature, submitfile):
    from sklearn.ensemble import RandomForestRegressor
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error

    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)
    params = {
        ‘n_estimators‘: 70,
        ‘max_depth‘: 13,
        ‘min_samples_split‘: 10,
        ‘min_samples_leaf‘: 10,
        ‘max_features‘: 7
    }
    model = RandomForestRegressor(**params)
    model.fit(X_train, y_train)
    # 对测试集进行预测
    y_pred = model.predict(X_test)
    # 计算准确率
    MSE = mean_squared_error(y_test, y_pred)
    RMSE = np.sqrt(MSE)
    print(RMSE)

    submit = pd.read_csv(submitfile)
    submit[‘y‘] = model.predict(test_feature)
    submit.to_csv(‘my_random_forest_prediction1.csv‘, index=False)

def random_forest_parameter_tuning1(feature_data, label_data, test_feature):
    from sklearn.ensemble import RandomForestRegressor
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error
    from sklearn.model_selection import GridSearchCV

    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)
    param_test1 = {
        ‘n_estimators‘: range(10, 71, 10)
    }
    model = GridSearchCV(estimator=RandomForestRegressor(
        min_samples_split=100, min_samples_leaf=20, max_depth=8, max_features=‘sqrt‘,
        random_state=10), param_grid=param_test1, cv=5
    )
    model.fit(X_train, y_train)
    # 对测试集进行预测
    y_pred = model.predict(X_test)
    # 计算准确率
    MSE = mean_squared_error(y_test, y_pred)
    RMSE = np.sqrt(MSE)
    print(RMSE)
    return model.best_score_, model.best_params_

def random_forest_parameter_tuning2(feature_data, label_data, test_feature):
    from sklearn.ensemble import RandomForestRegressor
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error
    from sklearn.model_selection import GridSearchCV

    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)
    param_test2 = {
        ‘max_depth‘: range(3, 14, 2),
        ‘min_samples_split‘: range(50, 201, 20)
    }
    model = GridSearchCV(estimator=RandomForestRegressor(
        n_estimators=70, min_samples_leaf=20, max_features=‘sqrt‘, oob_score=True,
        random_state=10), param_grid=param_test2, cv=5
    )
    model.fit(X_train, y_train)
    # 对测试集进行预测
    y_pred = model.predict(X_test)
    # 计算准确率
    MSE = mean_squared_error(y_test, y_pred)
    RMSE = np.sqrt(MSE)
    print(RMSE)
    return model.best_score_, model.best_params_

def random_forest_parameter_tuning3(feature_data, label_data, test_feature):
    from sklearn.ensemble import RandomForestRegressor
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error
    from sklearn.model_selection import GridSearchCV

    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)
    param_test3 = {
        ‘min_samples_split‘: range(10, 90, 20),
        ‘min_samples_leaf‘: range(10, 60, 10),
    }
    model = GridSearchCV(estimator=RandomForestRegressor(
        n_estimators=70, max_depth=13, max_features=‘sqrt‘, oob_score=True,
        random_state=10), param_grid=param_test3, cv=5
    )
    model.fit(X_train, y_train)
    # 对测试集进行预测
    y_pred = model.predict(X_test)
    # 计算准确率
    MSE = mean_squared_error(y_test, y_pred)
    RMSE = np.sqrt(MSE)
    print(RMSE)
    return model.best_score_, model.best_params_

def random_forest_parameter_tuning4(feature_data, label_data, test_feature):
    from sklearn.ensemble import RandomForestRegressor
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error
    from sklearn.model_selection import GridSearchCV

    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)
    param_test4 = {
        ‘max_features‘: range(3, 9, 2)
    }
    model = GridSearchCV(estimator=RandomForestRegressor(
        n_estimators=70, max_depth=13, min_samples_split=10, min_samples_leaf=10, oob_score=True,
        random_state=10), param_grid=param_test4, cv=5
    )
    model.fit(X_train, y_train)
    # 对测试集进行预测
    y_pred = model.predict(X_test)
    # 计算准确率
    MSE = mean_squared_error(y_test, y_pred)
    RMSE = np.sqrt(MSE)
    print(RMSE)
    return model.best_score_, model.best_params_


if __name__ == ‘__main__‘:
    trainfile = ‘data/train.csv‘
    testfile = ‘data/test.csv‘
    submitfile = ‘data/sample_submit.csv‘
    feature_data, label_data, test_feature = load_data(trainfile, testfile)
    random_forest_train(feature_data, label_data, test_feature, submitfile)

参考文献：https://www.jianshu.com/p/748b6c35773d

数据竞赛实战（3）——公共自行车使用量预测

标签：count des idt sel 网格删除 6.2 mem 9.1

原文地址：https://www.cnblogs.com/wj-1314/p/10620131.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行

数据竞赛实战（3）——公共自行车使用量预测

前言

1，背景介绍

2，任务类型

3，数据文件说明

4，数据变量说明

5，评估方法

6，完整代码，请移步小编的GitHub

数据预处理

1，观察数据有没有缺失值

2，观察每个变量的基础描述信息

3，查看相关系数

模型训练及其结果展示

1，标杆模型：简单线性回归模型

2，决策树回归模型

3，Xgboost回归模型

4，Xgboost回归模型调参过程

2，对于给定的学习速率和决策树数量，进行决策树特定参数调优（max_depth，min_child_weight，gamma，subsample，colsample_bytree）。在确定一棵树的过程中，我们可以选择不同的参数。

3，Xgboost的正则化参数的调优。（lambda，alpha）。这些参数可以降低模型的复杂度，从而提高模型的表现。

4，降低学习速率，确定理想参数。

5，Xgboost使用GridSearchCV调参过程

5.1，Xgboost 的默认参数如下（在sklearn库中的默认参数）：

5.2，首先调n_estimators

5.3，调参 max_depth和min_child_weight

5.4，gamma参数调优

5.5，调整subsample 和 colsample_bytree 参数

5.6，正则化参数调优

5.6，汇总出我们搜索到的最佳参数，然后训练

6，随机森林回归模型

7，随机森林回归模型调参过程

7.1 使用gridsearchcv探索n_estimators的最佳值

7.2 对决策树最大深度 max_depth 和内部节点再划分所需要的最小样本数求最佳值

7.3 求内部节点再划分所需要的最小样本数min_samples_split和叶子节点最小样本数min_samples_leaf的最佳参数

7.4 求最大特征数max_features的最佳参数

7.5 汇总出我们搜索到的最佳参数，然后训练

7.6 所有代码如下：

4，数据变量说明　

6，随机森林回归模型　