标签:clu when idt tmp 二次 bsp memset output wal
Input
Output
Sample Input
1 5 1 4 2 6 8 10 3 4 7 10
Sample Output
4
这道题我是参考大佬博客的,一开始我对这道题完全不知道怎么下手,百度了一下,发现是用离散化+线段树,其实我一开始还不知离散化是什么,又去学习了离散化再来写这道题;
下面是博主的分析:
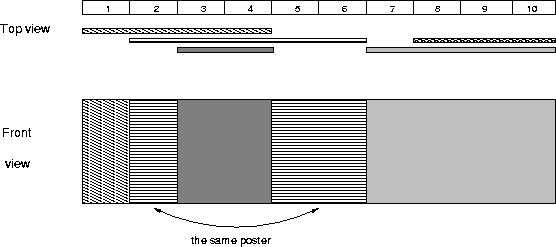
题意:贴海报,海报可以覆盖,会给出你每张海报的长款,然后问你最后还能看到几张海报。
我做这道题遇到的坑点,第一点离散化,第二点线段树用的不熟练
解法:离散化,如下面的例子(题目的样例),因为单位1是一个单位长度,将下面的
1 2 3 4 6 7 8 10
— — — — — — — —
1 2 3 4 5 6 7 8
离散化 X[1] = 1; X[2] = 2; X[3] = 3; X[4] = 4; X[5] = 6; X[6] = 7; X[7] = 8,X[8] = 10;
于是将一个很大的区间映射到一个较小的区间之中了,然后再对每一张海报依次更新在宽度为1~8的墙上(用线段树),
最后统计不同颜色的段数。但是只是这样简单的离散化是错误的,
如三张海报为:1~10 1~4 6~10离散化时 X[ 1 ] = 1, X[ 2 ] = 4, X[ 3 ] = 6, X[ 4 ] = 10
第一张海报时:墙的1~4被染为1;
第二张海报时:墙的1~2被染为2,3~4仍为1
;第三张海报时:墙的3~4被染为3,1~2仍为2。
最终,第一张海报就显示被完全覆盖了,于是输出2,但实际上明显不是这样,正确输出为3。
新的离散方法为:在相差大于1的数间加一个数,例如在上面1 4 6 10中间加5(算法中实际上1,4之间,6,10之间都新增了数的)
X[ 1 ] = 1, X[ 2 ] = 4, X[ 3 ] = 5, X[ 4 ] = 6, X[ 5 ] = 10
这样之后,第一次是1~5被染成1;第二次1~2被染成2;第三次4~5被染成3最终,1~2为2,3为1,4~5为3,于是输出正确结果3。
代码如下:
1 #include<iostream> 2 #include<stdio.h> 3 #include<algorithm> 4 #include<string.h> 5 using namespace std; 6 7 const int MAXN = 20005; 8 int T; 9 int N; 10 int x[MAXN] , y[MAXN]; 11 int lisan[MAXN*3]; 12 bool vis[MAXN*3]; 13 int tree[MAXN*16]; //离散化要开16倍空间 14 int size ; 15 int num = 0; 16 int tmp; 17 int ans ; 18 void pushdown(int rt ) 19 { 20 tree[rt*2] = tree[rt]; 21 tree[rt*2+1] = tree[rt]; 22 tree[rt] = 0; 23 } 24 void Update(int tpx ,int tpy ,int value, int l ,int r ,int rt) 25 { 26 if(l>=tpx&&r<=tpy) 27 { 28 tree[rt] = value; 29 return; 30 } 31 if(tree[rt]!=0) 32 pushdown(rt); 33 int m = (l+r)/2; 34 35 if(tpx<=m) 36 { 37 Update(tpx,tpy,value,l,m,rt*2); 38 } 39 if(tpy>m) 40 { 41 Update(tpx,tpy,value,m+1,r,rt*2+1); 42 } 43 44 } 45 void Query(int l ,int r ,int rt) 46 { 47 if(tree[rt]!=0) 48 { 49 if(!vis[tree[rt]]) 50 { 51 ans++; 52 vis[tree[rt]] = 1; 53 } 54 return ; 55 } 56 if(l==r) 57 return; 58 if(tree[rt]!=0) 59 { 60 pushdown(rt); 61 } 62 int m = (l+r)/2; 63 Query(l,m,rt*2); 64 Query(m+1,r,rt*2+1); 65 } 66 67 int main() 68 { 69 scanf("%d",&T); 70 while(T--) 71 { 72 scanf("%d",&N); 73 num = 0; 74 memset(tree,0,sizeof(tree)); 75 memset(vis,0,sizeof(vis)); 76 for(int i = 1 ; i <= N ;i++) 77 { 78 scanf("%d%d",&x[i],&y[i]); 79 lisan[num++] = x[i]; 80 lisan[num++] = y[i]; 81 } 82 sort(lisan,lisan+num); //排序后离散化 83 size = unique(lisan,lisan+num)-lisan; //获得离散化后的长度 84 tmp = size; 85 for(int i = 1 ; i < tmp ;i++) 86 { 87 if(lisan[i]-lisan[i-1]>1) //这样离散化才正确;见上面分析; 88 { 89 lisan[size++] = lisan[i-1] + 1; 90 } 91 } 92 sort(lisan,lisan+size); //再排序一次 93 for(int i = 1 ; i <= N ;i++ ) 94 { 95 int tpx = lower_bound(lisan,lisan+size,x[i])-lisan;//获取位置 96 int tpy = lower_bound(lisan,lisan+size,y[i])-lisan; 97 Update(tpx,tpy,i,0,size-1,1); 98 } 99 ans = 0 ; 100 Query(0,size-1,1); 101 printf("%d\n",ans); 102 } 103 return 0; 104 }
POJ - 2528Mayor's posters (离散化+线段树区间覆盖)
标签:clu when idt tmp 二次 bsp memset output wal
原文地址:https://www.cnblogs.com/yewanting/p/10800301.html