标签:总结 ati 添加 学习 字符 数据存储 mic hid return
通过前面的学习知道,具有“一对一”逻辑关系的数据,最佳的存储方式是使用线性表。那么,什么是线性表呢?



{1,2,3,4,5},数据最终的存储状态如图 1 所示:

typedef struct Table{ int * head;//声明了一个名为head的长度不确定的数组,也叫“动态数组” int length;//记录当前顺序表的长度 int size;//记录顺序表分配的存储容量 }table;
注意,head 是我们声明的一个未初始化的动态数组,不要只把它看做是普通的指针。
接下来开始学习顺序表的初始化,也就是初步建立一个顺序表。建立顺序表需要做如下工作:
因此,C 语言实现代码如下:
#define Size 5 //对Size进行宏定义,表示顺序表申请空间的大小 table initTable(){ table t; t.head=(int*)malloc(Size*sizeof(int));//构造一个空的顺序表,动态申请存储空间 if (!t.head) //如果申请失败,作出提示并直接退出程序 { printf("初始化失败"); exit(0); } t.length=0;//空表的长度初始化为0 t.size=Size;//空表的初始存储空间为Size return t; }
我们看到,整个顺序表初始化的过程被封装到了一个函数中,此函数返回值是一个已经初始化完成的顺序表。这样做的好处是增加了代码的可用性,也更加美观。与此同时,顺序表初始化过程中,要注意对物理空间的申请进行判断,对申请失败的情况进行处理,这里只进行了“输出提示信息和强制退出”的操作,可以根据你自己的需要对代码中的 if 语句进行改进。
通过在主函数中调用 initTable 语句,就可以成功创建一个空的顺序表,与此同时我们还可以试着向顺序表中添加一些元素,C 语言实现代码如下:
#include<stdio.h> #include<stdlib.h> #define Size 5 //定义一个顺序表 typedef struct table{ int *head;//用于定义数组头地址 int length;//记录当前顺序表的长度 int size;//记录顺序表的存储容量 }table; //初始化顺序表 table initTable() { table t; t.head = (int*)malloc(Size * sizeof(int));//动态申请存储空间 if (!t.head) { printf("顺序表初始化是被失败"); exit(0); } t.length = 0;//空表长度初始化为0 t.size = Size;//空表可以存储元素个数 return t; } //输出顺序表中元素函数 void display(table t) { for (int i = 0; i < t.length;i++) { printf("%d ",t.head[i]); } printf("\n"); } int main() { table t = initTable(); //向顺序表中添加元素 for (int i = 1; i <= Size;i++) { t.head[i - 1] = i; t.length++; } printf("顺序表中存储元素分别是:\n"); display(t); return 0; }
程序运行结果如下:
顺序表中存储的元素分别是:
1 2 3 4 5
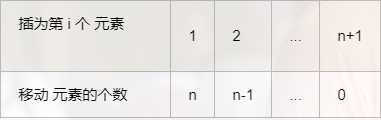
{1,2,3,4,5} 的第 3 个位置上插入元素 6,实现过程如下:



//插入函数,其中,elem为插入的元素,add为插入到顺序表的位置 table addTable(table t,int elem,int add) { //判断插入本身是否存在问题(如果插入元素位置比整张表的长度+1还大(如果相等,是尾随的情况),或者插入的位置本身不存在,程序作为提示并自动退出) if (add>t.length+1||add<1) { printf("插入位置有问题"); return t; } //做插入操作时,首先需要看顺序表是否有多余的存储空间提供给插入的元素,如果没有,需要申请 if (t.length==t.size) { t.head=(int *)realloc(t.head, (t.size+1)*sizeof(int)); if (!t.head) { printf("存储分配失败"); return t; } t.size+=1; } //插入操作,需要将从插入位置开始的后续元素,逐个后移 for (int i=t.length-1; i>=add-1; i--) { t.head[i+1]=t.head[i]; } //后移完成后,直接将所需插入元素,添加到顺序表的相应位置 t.head[add-1]=elem; //由于添加了元素,所以长度+1 t.length++; return t; }
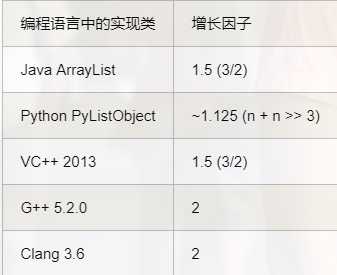
注意,动态数组额外申请更多物理空间使用的是 realloc 函数。并且,在实现后续元素整体后移的过程,目标位置其实是有数据的,还是 3,只是下一步新插入元素时会把旧元素直接覆盖。
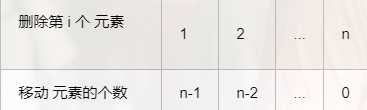
后续元素整体前移一个位置,会直接将目标元素删除,可间接实现删除元素的目的。
{1,2,3,4,5} 中删除元素 3 的过程如图 4 所示:

//删除指定元素 table deltable(table t,int del) { //add表示顺序表中删除元素的位置 if (del>t.length|| del<1) { printf("被删除的元素有误"); exit(0); } //删除操作 for (int i = del; i < t.length;i++) { t.head[i - 1] = t.head[i]; } t.length--; return t; }
顺序表中查找目标元素,可以使用多种查找算法实现,比如说二分查找算法、插值查找算法等。
这里,我们选择顺序查找算法,具体实现代码为:
//查找函数,其中,elem表示要查找的数据元素的值 int selectTable(table t,int elem){ for (int i=0; i<t.length; i++) { if (t.head[i]==elem) { return i+1; } } return -1;//如果查找失败,返回-1 }
顺序表更改元素的实现过程是:
顺序表更改元素的 C 语言实现代码为
//更改函数,其中,elem为要更改的元素,newElem为新的数据元素 table amendTable(table t,int elem,int newElem){ int add=selectTable(t, elem); t.head[add-1]=newElem;//由于返回的是元素在顺序表中的位置,所以-1就是该元素在数组中的下标 return t; }
以上是顺序表使用过程中最常用的基本操作,这里给出本节完整的实现代码:

#include<stdio.h> #include<stdlib.h> #define Size 5 //定义一个顺序表 typedef struct table{ int *head;//用于定义数组头地址 int length;//记录当前顺序表的长度 int size;//记录顺序表的存储容量 }table; //初始化顺序表 table initTable() { table t; t.head = (int*)malloc(Size * sizeof(int));//动态申请存储空间 if (!t.head) { printf("顺序表初始化是被失败"); exit(0); } t.length = 0;//空表长度初始化为0 t.size = Size;//空表可以存储元素个数 return t; } //插入函数,elem:插入的元素 add:插入到顺序表的位置 table addTable(table t, int elem,int add) { /*1,判断插入本身是否存在问题 如果插入元素位置比整张表的长度+1还大,(如果相等,就是尾随的情况) 或者插入位置本身不存在程序作为提示,自动退出*/ if (add > t.length + 1 || add < 1) { printf("插入位置有问题"); return t; } /*做插入时,首先要看顺序表是否有多余的存储空间提供给插入的元素, 如果没有需要申请 */ if (t.length==t.size) { t.head = (int*)realloc(t.head,(t.size+1)*sizeof(int)); if (!t.head) { printf("存储分配失败"); exit(0); } t.size += 1; } //插入操作,需要从插入位置开始的后续元素,逐个后移 for (int i = t.length - 1; i >= add - 1;i--) { t.head[i + 1] = t.head[i]; } //后移完成后直接将所需元素,添加到顺序表相应的位置 t.head[add - 1] = elem; //由于添加了元素,所以长度+1 t.length++; return t; } //删除指定元素 table deltable(table t,int del) { //add表示顺序表中删除元素的位置 if (del>t.length|| del<1) { printf("被删除的元素有误"); exit(0); } //删除操作 for (int i = del; i < t.length;i++) { t.head[i - 1] = t.head[i]; } t.length--; return t; } //查找元素,elem表示要找的数据元素的值 int findByElem(table t,int elem) { for(int i=0;i < t.length;i++){ if (t.head[i]==elem) { return i + 1; } } return -1;//如果查找失败返回-1 } //更改顺序表中某个元素 table updateTable(table t,int oldElem,int newElem) { int n = findByElem(t,oldElem);//找出old元素所在位置 t.head[n - 1] = newElem;//由于返回的是元素在顺序表中的位置,所以-1就是元素在数组的下标 return t; } //输出顺序表中元素函数 void display(table t) { for (int i = 0; i < t.length;i++) { printf("%d ",t.head[i]); } printf("\n"); } int main() { table t = initTable(); //向顺序表中添加元素 for (int i = 1; i <= Size;i++) { t.head[i - 1] = i; t.length++; } printf("原顺序表中存储元素顺序是:\n"); display(t); table t1=addTable(t,8,2); printf("添加元素后是:\n"); display(t1); t1=deltable(t1,2); printf("删除add位上的元素后:\n"); display(t1); int n=findByElem(t1,4); printf("查找元素4的位置:%d \n",n); t1 = updateTable(t1,1,9); printf("元素1修改为9后遍历:\n"); display(t1); return 0; }
程序运行结果为:

总结:
插入元素,时间复杂度 O(n)
标签:总结 ati 添加 学习 字符 数据存储 mic hid return
原文地址:https://www.cnblogs.com/2019wxw/p/10802048.html