标签:就是 NPU click sed 怎么 cut 节点 eof event

#include<bits/stdc++.h> using namespace std; //input by bxd #define rep(i,a,b) for(int i=(a);i<=(b);i++) #define repp(i,a,b) for(int i=(a);i>=(b);--i) #define RI(n) scanf("%d",&(n)) #define RII(n,m) scanf("%d%d",&n,&m) #define RIII(n,m,k) scanf("%d%d%d",&n,&m,&k) #define RS(s) scanf("%s",s); #define ll long long #define pb push_back #define REP(i,N) for(int i=0;i<(N);i++) #define CLR(A,v) memset(A,v,sizeof A) ////////////////////////////////// #define inf 0x3f3f3f3f const int N=100010; const int M=10*N; int n,m; int pos,head[M]; struct Edge { int to,nex; }edge[M]; void add(int a,int b) { edge[++pos].nex=head[a]; head[a]=pos; edge[pos].to=b; } int dfn[N],tot,low[N],cut[N]; void init() { tot=pos=0; CLR(head,0); CLR(dfn,0); CLR(cut,0); } void tarjan(int x,int fa) { dfn[x]=low[x]=++tot; int son=0; for(int i=head[x];i;i=edge[i].nex) { int v=edge[i].to; if(!dfn[v]) { tarjan(v,fa); low[x]=min(low[x],low[v]); if(low[v]>=dfn[x]&&x!=fa) cut[x]=1; if(v==fa) son++; } low[x]=min(low[x],dfn[v]); } if(son>=2&&x==fa) cut[x]=1; } int main() { int n,m; RII(n,m); init(); rep(i,1,m) { int a,b;RII(a,b); add(a,b);add(b,a); } rep(i,1,n) if(!dfn[i]) tarjan(i,i); int cnt=0; rep(i,1,n) if(cut[i]) cnt++; cout<<cnt<<endl; rep(i,1,n) if(cut[i]) cout<<i<<" "; }
可以使用Tarjan算法求割点(注意,还有一个求连通分量的算法也叫Tarjan算法,与此算法类似)。(Tarjan,全名Robert Tarjan,美国计算机科学家。)
首先选定一个根节点,从该根节点开始遍历整个图(使用DFS)。
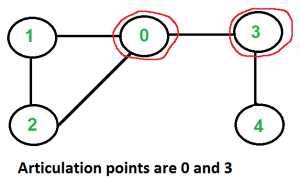
对于根节点,判断是不是割点很简单——计算其子树数量,如果有2棵即以上的子树,就是割点。因为如果去掉这个点,这两棵子树就不能互相到达。
对于非根节点,判断是不是割点就有些麻烦了。我们维护两个数组dfn[]和low[],dfn[u]表示顶点u第几个被(首次)访问,low[u]表示顶点u及其子树中的点,通过非父子边(回边),能够回溯到的最早的点(dfn最小)的dfn值(但不能通过连接u与其父节点的边)。对于边(u, v),如果low[v]>=dfn[u],此时u就是割点。
但这里也出现一个问题:怎么计算low[u]。
假设当前顶点为u,则默认low[u]=dfn[u],即最早只能回溯到自身。
有一条边(u, v),如果v未访问过,继续DFS,DFS完之后,low[u]=min(low[u], low[v]);
如果v访问过(且u不是v的父亲),就不需要继续DFS了,一定有dfn[v]<dfn[u],low[u]=min(low[u], dfn[v])。
标签:就是 NPU click sed 怎么 cut 节点 eof event
原文地址:https://www.cnblogs.com/bxd123/p/10802887.html