标签:str lse == can 数学 编写 一段 rem 面积
1、编写由三角形三边求面积的函数
2、编写求N的阶层
3、求两个整数的最大公约数
4、打印输出的指定图形
5、模块化程序设计
姓名:张顺利 实验地点:第一教学楼514教室 实验时间:4月30日
调用gcd()函数求两个整数的最大公约数;
调用trangle()函数输出三角形;
掌握C语言中定义函数的方法;
1.问题描述:编写程序,从键盘输入三角形的3条边,调用三角形函数求出其面积,并输出结果。
2.流程图:
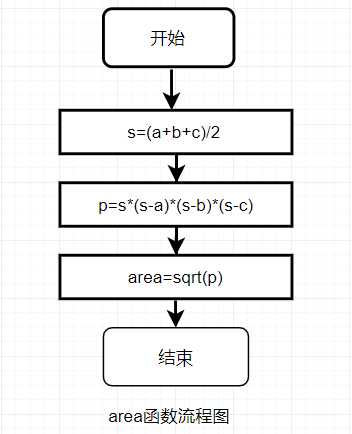
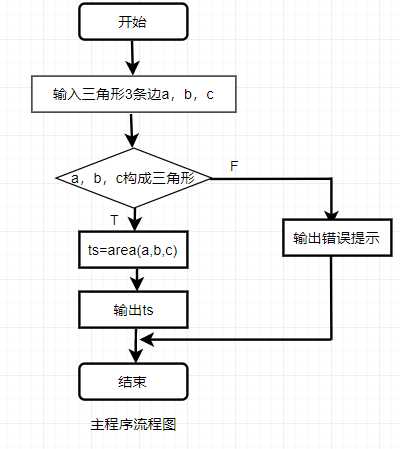
3.代码示例:
#include<math.h>
#include<stdio.h>
float area(float a,float b,float c)
{
float s,p,area;
s=(a+b+c)/2;
p=s*(s-a)*(s-b)*(s-c);
area=sqrt(p);
return(area);
}
main()
{
float x,y,z,ts;
printf("请输入三角形的三边:\n");
scanf("%f,%f,%f",&x,&y,&z);
ts=area(x,y,z);
if (x+y>=z&&x+z>=y&&y+z>=x)
printf("area=%f\n",ts);
else printf("data error!");
}
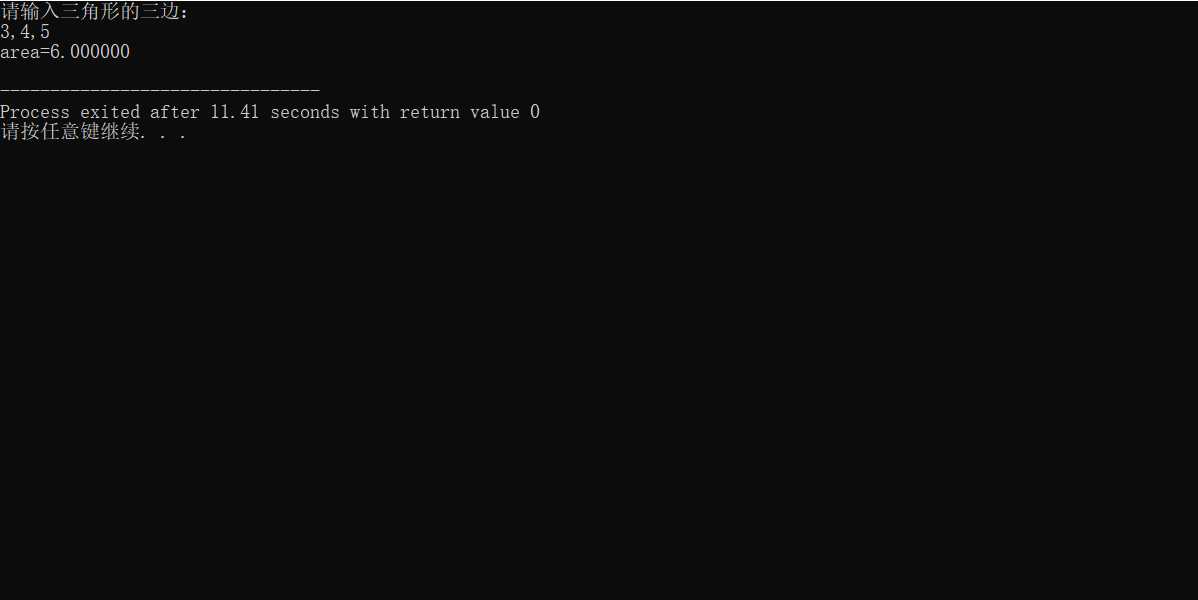
4.代码分析:这道题在主程序上方写了一段名为area的函数,在主程序就直接调用了这段函数,这个和我们在上学期学习的HTML和css的关系,我认为是差不多的,在主程序外写一段代码,在主程序中可以使主程序更加简便,保证了程序的顺序性,和简便性。但是我又发现我存在的一个问题,我认为这也是大多数同学一知半解的问题,就是单精度%f和双精度%d的区别到底是什么,为什么我有时候用%d的时候就无法显示,用了%f才能显示,比如这道题。他们的用法到底是什么?我想向老师请教。
1.问题描述:编写函数,求出从主调函数传来的数值i的阶乘值,然后将其传出主调函数并输出。
2.流程图:
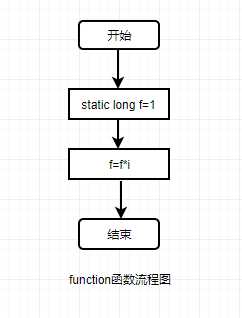
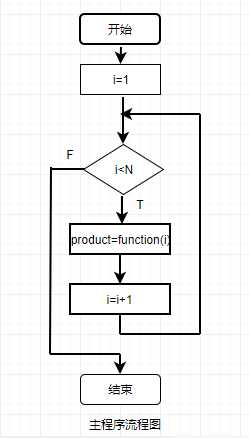
3.代码示例:
#include<stdio.h> #define N 5 long function(int i) { static long f=1; if(i>1) f=i*function(i-1); else return 1; return f; } main() { long product; int i; for(i=1; i<=N;i++) { product=function(i); printf("%d的阶乘是:%ld\n",i,product); } }
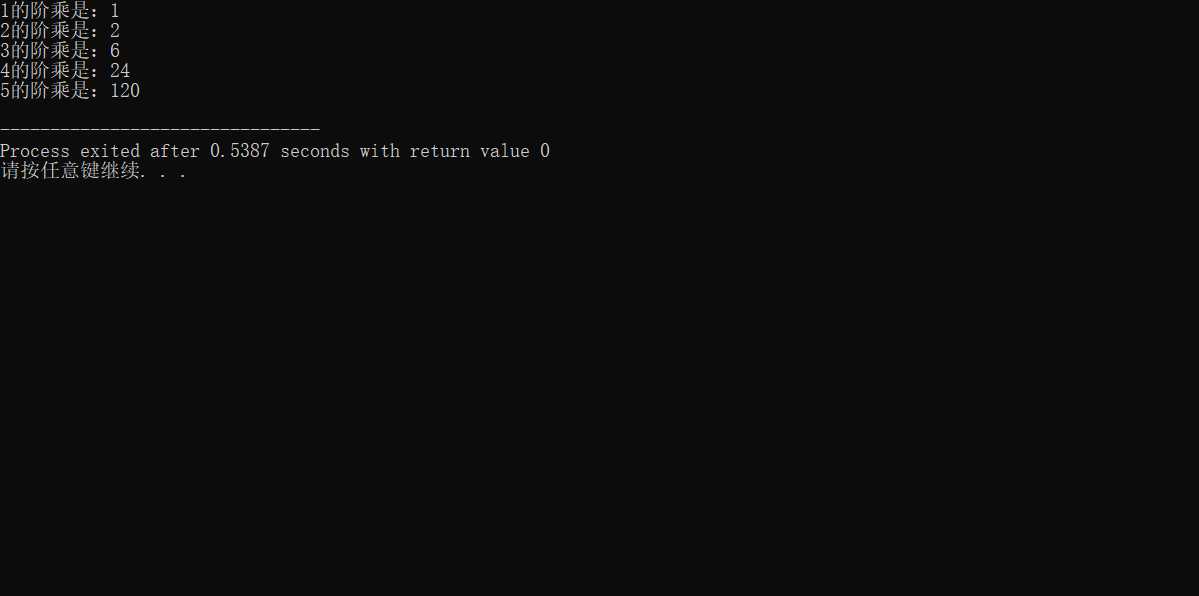
4.算法思考:这道题并不是很难,我认为他想考核的是函数的定义,以及函数算法的思考。函数首先要用“#define N 5”定义符号常量N,并代表数字5;并且用“static long f=1”定义局部静态变量f并赋初值1; 最后要调用函数function()求阶乘值,并将其赋product。
1.问题描述:编写程序,从键盘输入两个整数,调用gcd()函数求它们的最大公约数,并输出结果。
2.流程图:
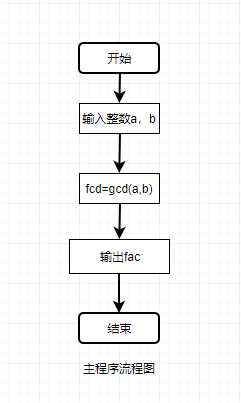
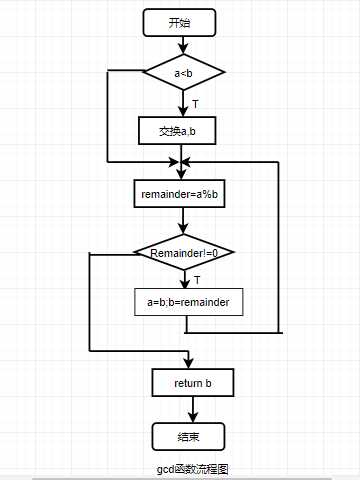
3.代码示例:
#include<stdio.h> int gcd(int a,int b) { int temp; int remainder; if(a<b) { temp=a; a=b; b=temp; } remainder=a%b; while(remainder!=0) { a=b; b=remainder; remainder=a%b; } return b; } main() { int x,y; int fac; printf("请输入两个整数:\n"); scanf("%d,%d",&x,&y); fac=gcd(x,y); printf("该两数的最大公约数是:%d",fac); }
4.代码思考:说实话,这道题我也挺懵的,因为我也不清楚怎么求最大公因数,只能按照流程图一步一步做,但还是出了不少意外,比如刚刚开始时,无法输出;再到后来加了break才输出,但老师说也是不对的,好在最后找到了正确的算法。但也暴露了我不少问题。
1.问题描述:输入整数n,输出高度为n的等边三角形。
2.流程图:
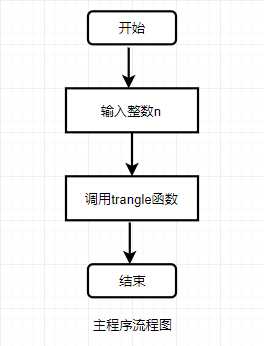
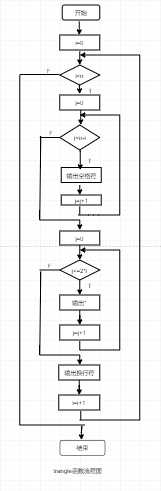
3.代码示例:
#include<stdio.h> trangle(int n) { int i,j; for (i=0;i<n;i++) { for (j=0;j<n-i;j++) { printf(" "); } for (j=0;j<=2*i;j++) { printf("*"); } printf("\n"); } } main() { int n; printf("请输入一个整数:"); scanf("%d",&n); printf("\n"); trangle(n); }
4.算法思考:这里又是单双精度的问题,我在这里用%f,结果就成了无限循环的空格,半天找不出问题,我还以为算法出了错,在那里改了半天算法;结果都没有用,只有我把%f改成%d,他才显示出来。我认为我这个问题不搞定,之后绝对还会抓狂。
1.问题描述:若正整数A的所有因子(包括1但不包括自身,下同)之和为B,而B的因子之和为A,则称A和B为一对亲密数。例如,6的因子之和为1+2+3=6,因此6与6为一对亲密数(即6自身构成一对亲密数);又如,220的因子之和为1+2+4+5+10+11+20+22+44+55+110=284,而284的因子之和为1+2+4+71+142=220,因此,220与284为一对亲密数。
求500以内的所有的亲密数对。
具体要求如下:
(1)编制一个函数facsum(m),返回给定正整数m的所有因子(包括1但不包括自身)之和。
(2)编制一个主函数,调用(1)中的函数facsum(),寻找并输出500以内的所有亲密数对。
(3)输出要有文字说明。在输出每对亲密数时,要求从小到大排列并去掉重复的亲密数对。
(4)所有函数中的循环均为for循环。
2.流程图:
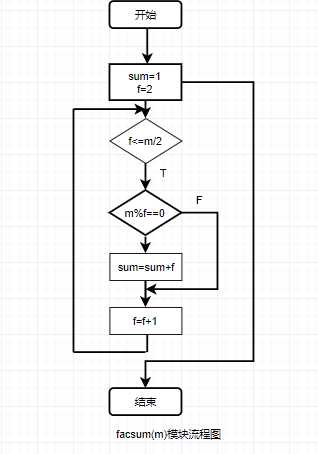
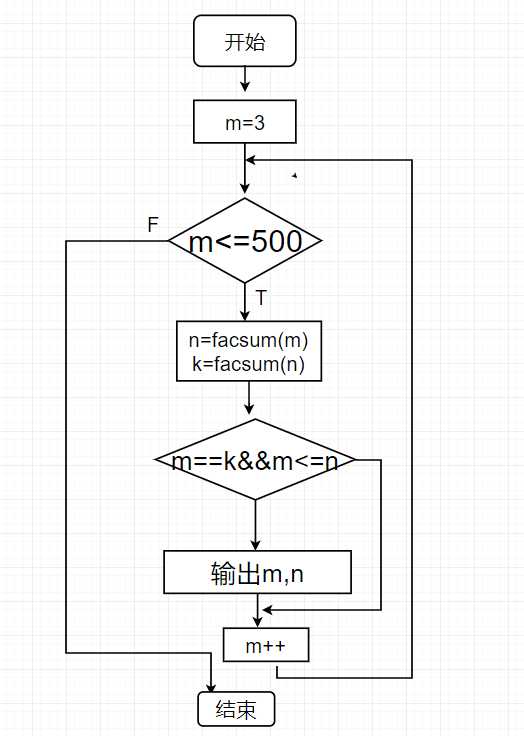
3.代码示例:
#include<stdio.h> int facsum(int m) { int sum=1,f=2; while(f<=m/2) { if(m%f==0) sum=sum+f; f++; } return sum; } main() { int m=3,n,k; while(m<=500) { n=facsum(m); k=facsum(n); if(m==k&&m<=n) printf("%d %d\n",m,n); m++; } }
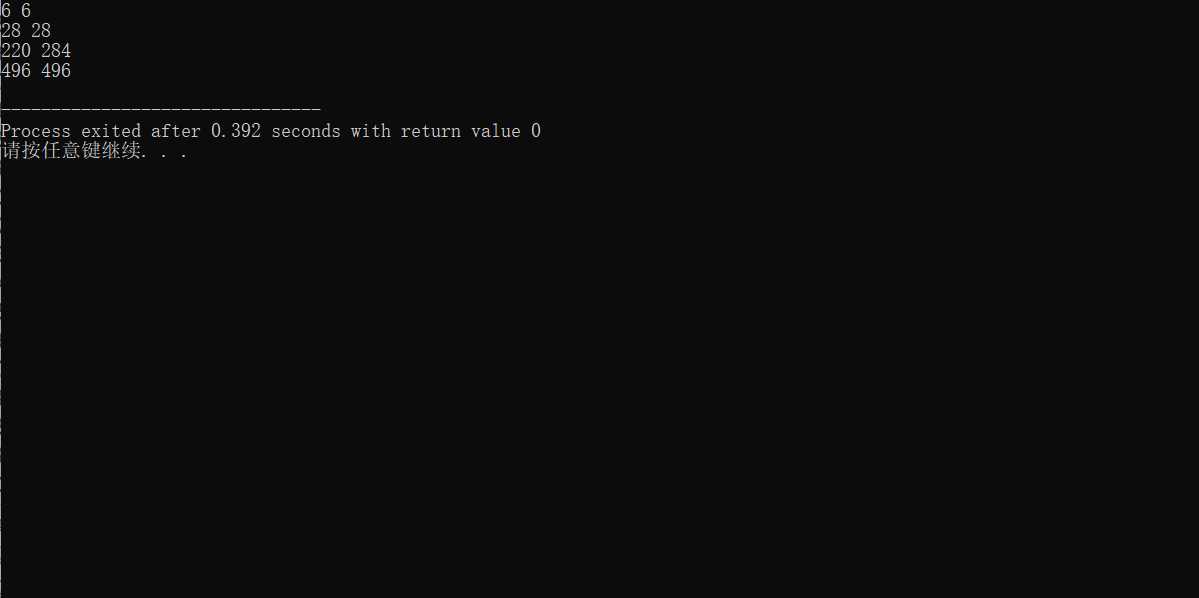
4.算法思考:在看懂了什么是亲密数对的情况下,这道题其实并不是很难,先做什么,后做什么在流程图里一眼就能懂,为什么要这么做,这步的意义有是什么,一目了然。
我认为我这次实验发现最大的问题是单双精度的用法和数学函数的常识较低,而我认为这两块会大大限制我对C语言的理解。所以我会在提问区发出疑问,希望老师和同学给我解答疑难。另外我认为本次实验其实不难,真正的难题其实是6.4.2(2)。我到现在都没有做出来,在这个五一长假中我希望能将这个代码成功实现。
标签:str lse == can 数学 编写 一段 rem 面积
原文地址:https://www.cnblogs.com/1403262085zsl/p/10804146.html