标签:.com blank 题目 style src 价值 printf 入队 name
有n种物品,用大小为m的包来装,问获取的最大价值为多少。其中,第 i 种物品的重量,价值,个数分别为 w[i],v[i],c[i].
那么,若f[i][j]表示考虑前 i 种物品,使用 j 的背包可获取的最大价值,状态转移方程为
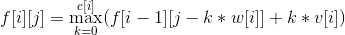
for(int i=1;i<=n;i++)
for(int k=1;k<=c[i];k++)
for(int j=0;j<=m;j++)
if(j-k*w[i]>=0)f[i][j]=max(f[i-1][j],f[i-1][j-k*w[i])+v[i]);
else f[i][j]=f[i-1][j];
考虑到,f[i][j1]可由f[i-1][j2]更新当且仅当j1,j2模w[i]同余。
那么,要更新每个f[i][j],只用在 j‘ 模w[i]同余地一系列f[i-1][j‘]中找,而且这一系列数的 j‘ 有都相差w[i],所以可以用一个单调队列来保存离 j 最近的c[i]个 j‘ 的最大值,队首保存用于更新的最优解,就可以直接找到最优的更新方案。
对于进队的条件:
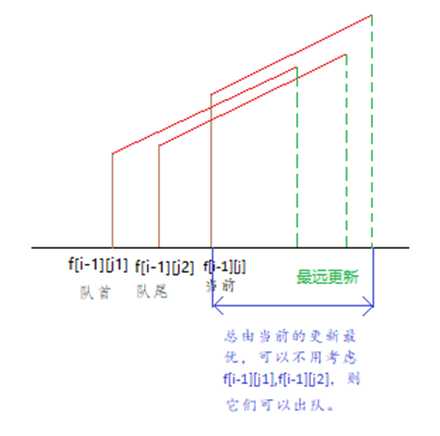
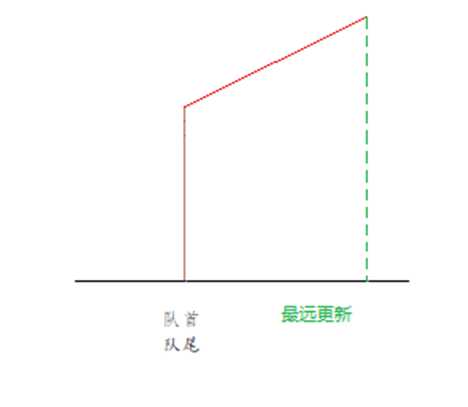
由于放同一种物品空间与价值成正比,则f[i-1][j]可以更新的背包空间为一条斜线段所覆盖的区域,起点即为点(j,f[i-1][j]),斜率即为价值比总量,而队中存的就是起点(我存了起点的横坐标)。若当前有要入队的起点,可以做如第一个图的比较,使用当前起点更新的范围是否涵盖了队尾元素,若涵盖了则弹出,否则将当前起点加入队中。
对于出队条件:当前要更新的背包空间已经超出了队首的最远更新范围。
这个题其实可以不加优化:-)
1 #include<bits/stdc++.h> 2 using namespace std; 3 int C,n,m,a[101],b[101],c[101],f[101][101]; 4 int dui[100000],hd,tl; 5 6 bool calc(int kj,int wp) 7 { 8 int maxa=c[wp]*a[wp]; 9 int tem=dui[hd+1]; 10 if(tem+maxa<kj)return 1; 11 return 0; 12 } 13 14 bool cc(int kj,int wp) 15 { 16 if(hd==tl)return 0; 17 int tem=dui[tl]; 18 if((kj-tem)/a[wp]*b[wp]<=f[wp-1][kj]-f[wp-1][tem])return 1; 19 return 0; 20 } 21 22 int main() 23 { 24 scanf("%d",&C); 25 for(int I=1;I<=C;I++) 26 { 27 memset(f,0,sizeof(f)); 28 scanf("%d%d",&n,&m); 29 for(int i=1;i<=m;i++)scanf("%d%d%d",&a[i],&b[i],&c[i]); 30 for(int i=1;i<=m;i++) 31 { 32 for(int ys=0;ys<a[i];ys++) 33 { 34 hd=0; 35 tl=0; 36 for(int j=ys;j<=n;j+=a[i]) 37 { 38 while((hd!=tl)&&calc(j,i)) 39 { 40 hd++; 41 } 42 if(hd!=tl) 43 { 44 int tem=dui[hd+1]; 45 f[i][j]=f[i-1][tem]+(j-tem)/a[i]*b[i]; 46 } 47 f[i][j]=max(f[i][j],f[i-1][j]); 48 while(cc(j,i))tl--; 49 tl++; 50 dui[tl]=j; 51 } 52 } 53 } 54 int ans=0; 55 for(int i=0;i<=n;i++) 56 { 57 for(int j=1;j<=m;j++) 58 ans=max(ans,f[j][i]); 59 } 60 printf("%d\n",ans); 61 } 62 return 0; 63 }
标签:.com blank 题目 style src 价值 printf 入队 name
原文地址:https://www.cnblogs.com/LiqgNonqfu/p/10800929.html