标签：hdu1067

Gap

Let‘s play a card game called Gap.
You have 28 cards labeled with two-digit numbers. The first digit (from 1 to 4) represents the suit of the card, and the second digit (from 1 to 7) represents the value of the card.

First, you shu2e the cards and lay them face up on the table in four rows of seven cards, leaving a space of one card at the extreme left of each row. The following shows an example of initial layout.



Next, you remove all cards of value 1, and put them in the open space at the left end of the rows: "11" to the top row, "21" to the next, and so on.

Now you have 28 cards and four spaces, called gaps, in four rows and eight columns. You start moving cards from this layout.



At each move, you choose one of the four gaps and fill it with the successor of the left neighbor of the gap. The successor of a card is the next card in the same suit, when it exists. For instance the successor of "42" is "43", and "27" has no successor.

In the above layout, you can move "43" to the gap at the right of "42", or "36" to the gap at the right of "35". If you move "43", a new gap is generated to the right of "16". You cannot move any card to the right of a card of value 7, nor to the right of a gap.

The goal of the game is, by choosing clever moves, to make four ascending sequences of the same suit, as follows.



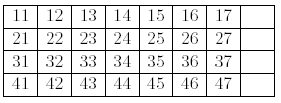
Your task is to find the minimum number of moves to reach the goal layout.

4

12 13 14 15 16 17 21
22 23 24 25 26 27 31
32 33 34 35 36 37 41
42 43 44 45 46 47 11

26 31 13 44 21 24 42
17 45 23 25 41 36 11
46 34 14 12 37 32 47
16 43 27 35 22 33 15

17 12 16 13 15 14 11
27 22 26 23 25 24 21
37 32 36 33 35 34 31
47 42 46 43 45 44 41

27 14 22 35 32 46 33
13 17 36 24 44 21 15
43 16 45 47 23 11 26
25 37 41 34 42 12 31

0
33
60
-1

题意：给定一张4X8的表格，求将其变换到目标状态需要的最少步数。

题解：将表格转换成字符串，空位用1表示，每一种表格用map映射下，剩下的事就是广搜了。

#include <stdio.h>
#include <string.h>
#include <string>
#include <queue>
#include <map>

using namespace std;

const char aimStr[] = {
	11, 12, 13, 14, 15, 16, 17, 1,
	21, 22, 23, 24, 25, 26, 27, 1,
	31, 32, 33, 34, 35, 36, 37, 1,
	41, 42, 43, 44, 45, 46, 47, 1, 0
};
struct Node {
	char str[36];
	int steps;
};
char buf[36];

void Move(Node &now, int val) {
	for(int i = 0; ; ++i)
		if(now.str[i] == val) {
			now.str[i] = 1;
			return;
		}
}

int BFS() {
	queue<Node> Q;
	Node tmp, now;
	strcpy(now.str, buf);
	now.steps = 0;
	Q.push(now);

	map<string, int> mp;
	int mpid = 1, i, j;
	mp[buf] = mpid++;
	if(mp[aimStr] == mp[buf]) return 0;
	mp[aimStr] = mpid++;

	while(!Q.empty()) {
		now = Q.front(); Q.pop();
		for(i = 0; i < 32; ++i) {
			if(now.str[i] == 1 && now.str[i-1] != 1 
				&& now.str[i-1] % 10 != 7) {
				tmp = now;
				Move(tmp, tmp.str[i-1] + 1);
				tmp.str[i] = tmp.str[i-1] + 1;
				++tmp.steps;
				if(mp[tmp.str] == mp[aimStr]) return tmp.steps;
				if(mp[tmp.str] == 0) {
					mp[tmp.str] = mpid++;
					Q.push(tmp);
				}
			}
		}
	}

	return -1;
}

int main() {
	// freopen("stdin.txt", "r", stdin);
	int n, i, j, k, tmp;
	scanf("%d", &n);
	while(n--) {
		for(i = k = 0; i < 4; ++i) {
			buf[k++] = (i + 1) * 10 + 1;
			for(j = 1; j < 8; ++j) {
				scanf("%d", &tmp);
				buf[k] = tmp;
				if(buf[k] % 10 == 1) 
					buf[k] = 1;
				++k;
			}
		}
		printf("%d\n", BFS());
	}
	return 0;
}

HDU1067 Gap 【BFS+MAP】

标签：hdu1067

原文地址：http://blog.csdn.net/chang_mu/article/details/40272845